【MATLAB线性插值实战指南】：掌握10个实战案例，轻松解决数据缺失难题

# 1. MATLAB线性插值简介

线性插值是一种广泛应用于数据处理和分析中的数学技术。它通过已知数据点之间的线性关系，来估计未知数据点的值。在MATLAB中，线性插值可以通过内置函数或自定义函数实现。

MATLAB内置的线性插值函数interp1提供了方便快捷的插值功能，其基本语法为：

y = interp1(x, y, xi)

其中，x为已知数据点的横坐标，y为已知数据点的纵坐标，xi为待插值点的横坐标。interp1函数会根据已知数据点，使用线性插值公式计算出xi对应的纵坐标y。

# 2. MATLAB线性插值理论基础

### 2.1 线性插值的原理和公式

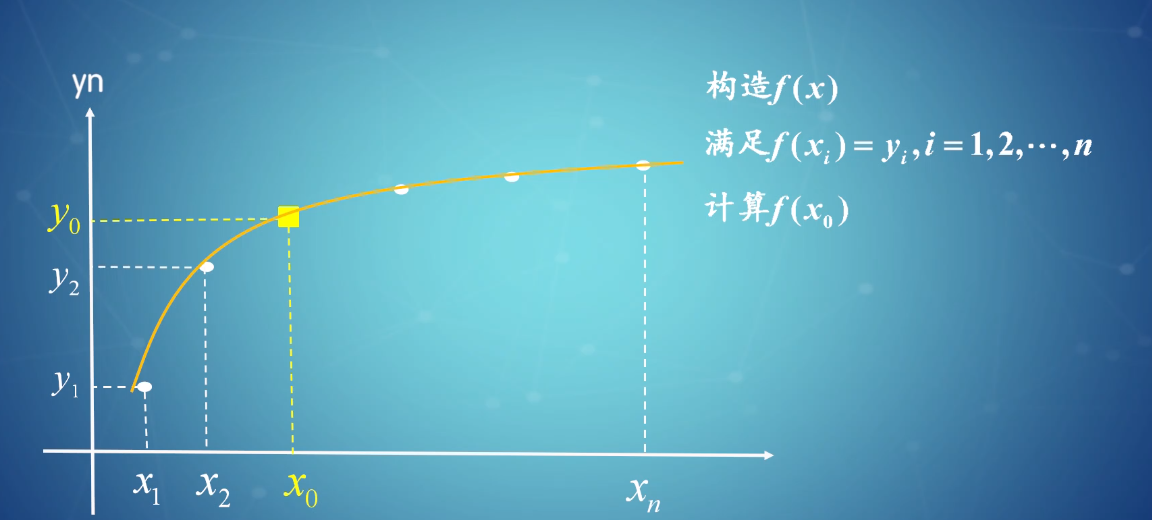
线性插值是一种用于估计未知数据点值的方法，其基本原理是假设在两个已知数据点之间，数据值的变化是线性的。给定一组已知数据点 $(x_0, y_0), (x_1, y_1), \cdots, (x_n, y_n)$，其中 $x_0 < x_1 < \cdots < x_n$，对于任意 $x \in [x_i, x_{i+1}] (i=0, 1, \cdots, n-1)$，其对应的插值值 $y$ 可以表示为：

$$y = y_i + \frac{x - x_i}{x_{i+1} - x_i} (y_{i+1} - y_i)$$

其中，$y_i$ 和 $y_{i+1}$ 分别是 $x_i$ 和 $x_{i+1}$ 对应的已知数据值。

### 2.2 线性插值的误差分析

线性插值的误差主要来自两个方面：

1. **截断误差：**这是由于将非线性函数用线性函数近似造成的误差。
2. **舍入误差：**这是由于计算机有限精度造成的误差。

截断误差的大小取决于插值函数与被插值函数的非线性程度，而舍入误差的大小取决于计算机的字长。

**截断误差的分析：**

假设被插值函数 $f(x)$ 在 $[x_i, x_{i+1}]$ 区间内二阶可导，则线性插值函数 $L(x)$ 的截断误差为：

$$R(x) = f(x) - L(x) = \frac{f''(\xi)}{2} (x - x_i)(x - x_{i+1})$$

其中，$\xi \in [x_i, x_{i+1}]$。

从公式中可以看出，截断误差与插值点之间的距离平方成正比，因此，减小插值点之间的距离可以有效减少截断误差。

**舍入误差的分析：**

舍入误差的大小与计算机的字长有关，一般情况下，计算机的字长为 32 位或 64 位。对于 32 位计算机，舍入误差的范围约为 $10^{-7}$，对于 64 位计算机，舍入误差的范围约为 $10^{-15}$。

**误差控制：**

为了控制线性插值的误差，可以采取以下措施：

1. 选择合适的插值点：插值点应尽可能均匀分布在插值区间内。
2. 使用高精度计算机：使用字长较大的计算机可以减小舍入误差。
3. 采用自适应插值算法：自适应插值算法可以根据误差大小自动调整插值点的位置，从而减小插值误差。

# 3.1 内置线性插值函数的使用

MATLAB 提供了内置的线性插值函数 `interp1`，它可以方便地对一维数据进行线性插值。`interp1` 函数的基本语法如下：

y = interp1(x, y, xi)

其中：

* `x`：已知数据点的自变量值
* `y`：已知数据点的因变量值
* `xi`：需要插值的自变量值

#### 3.1.1 interp1函数的基本语法和参数

`interp1` 函数支持多种插值方法，包括线性插值、最近邻插值、三次样条插值等。默认情况下，`interp1` 函数使用线性插值方法。

除了基本语法之外，`interp1` 函数还提供了多种参数，可以控制插值的行为。常用的参数包括：

* `method`：插值方法，可以取值为 'linear'（线性插值）、'nearest'（最近邻插值）、'spline'（三次样条插值）等。
* `extrap`：插值超出范围的行为，可以取值为 'extrap'（超出范围时进行外推）、'hold'（超出范围时保持边界值）等。
* `fillvalue`：超出范围时的填充值，当 `extrap` 为 'hold' 时有效。

#### 3.1.2 interp1函数的高级应用

除了基本功能之外，`interp1` 函数还支持一些高级应用，例如：

* **多维插值：**`interp1` 函数可以通过重复使用来实现多维插值。例如，对于二维数据，可以先对每一行进行插值，然后再对每一列进行插值。
* **非均匀网格插值：**`interp1` 函数可以通过指定 `x` 和 `xi` 的非均匀网格来实现非均匀网格插值。
* **自定义插值函数：**`interp1` 函数可以通过自定义插值函数来实现自定义的插值方法。

### 3.2 自定义线性插值函数的实现

除了使用内置的 `interp1` 函数之外，也可以自定义实现线性插值函数。自定义插值函数可以提供更大的灵活性，例如：

* 可以实现更复杂的插值方法，例如二次插值、三次插值等。
* 可以针对特定的数据类型或应用场景进行优化。
* 可以方便地集成到自定义的代码中。

#### 3.2.1 线性插值算法的实现

线性插值算法的实现非常简单，其核心思想是通过已知数据点之间的直线进行插值。对于两个已知数据点 `(x1, y1)` 和 `(x2, y2)`，在自变量 `xi` 处的插值值 `yi` 可以通过以下公式计算：

yi = y1 + (y2 - y1) * (xi - x1) / (x2 - x1)

#### 3.2.2 自定义插值函数的性能优化

自定义插值函数的性能优化可以通过以下方法实现：

* **向量化计算：**使用向量化操作来避免循环，可以显著提高性能。
* **缓存数据：**将经常使用的数据缓存起来，可以减少数据访问时间。
* **并行计算：**对于大规模数据，可以使用并行计算来加速插值过程。

# 4. MATLAB线性插值实战案例

### 4.1 缺失数据插值

#### 4.1.1 时间序列数据的插值

时间序列数据是指按时间顺序收集的一系列数据点。缺失数据是时间序列分析中常见的问题，可以使用线性插值来填补这些缺失值。

**代码示例：**

% 生成时间序列数据
t = 0:0.1:10;
y = sin(t) + randn(size(t));

% 在数据中引入缺失值
y(5:10) = NaN;

% 使用线性插值填充缺失值
y_interp = interp1(t, y, t, 'linear');

% 绘制原始数据和插值后的数据
plot(t, y, 'o', t, y_interp, '-');
legend('原始数据', '插值数据');

**逻辑分析：**

* `interp1` 函数的基本语法为 `interp1(x, y, xi, method)`，其中 `x` 为原始数据的自变量，`y` 为原始数据的因变量，`xi` 为需要插值的自变量，`method` 为插值方法。
* `linear` 方法表示使用线性插值。
* 插值后的数据 `y_interp` 中，缺失值已被填充为线性插值的结果。

#### 4.1.2 图像数据的插值

图像数据通常以像素矩阵的形式存储，缺失像素会影响图像的质量。线性插值可以用来填充缺失像素，恢复图像的完整性。

**代码示例：**

% 读取图像
img = imread('image.jpg');

% 在图像中引入缺失像素
img(100:200, 100:200) = NaN;

% 使用线性插值填充缺失像素
img_interp = interp2(img, 'linear');

% 显示原始图像和插值后的图像
subplot(1,2,1);
imshow(img);
title('原始图像');

subplot(1,2,2);
imshow(img_interp);
title('插值后的图像');

**逻辑分析：**

* `interp2` 函数的基本语法为 `interp2(x, y, z, xi, yi, method)`，其中 `x` 和 `y` 为原始数据的自变量，`z` 为原始数据的因变量，`xi` 和 `yi` 为需要插值的自变量，`method` 为插值方法。
* `linear` 方法表示使用线性插值。
* 插值后的图像 `img_interp` 中，缺失像素已被填充为线性插值的结果。

### 4.2 数据平滑和降噪

#### 4.2.1 线性插值用于数据平滑

数据平滑是指去除数据中的噪声和毛刺，使数据更平滑。线性插值可以用来平滑数据，通过将相邻数据点连接起来形成一条平滑曲线。

**代码示例：**

% 生成带有噪声的数据
data = randn(100, 1) + 0.5 * sin(1:100);

% 使用线性插值平滑数据
data_smooth = interp1(1:100, data, 1:0.1:100, 'linear');

% 绘制原始数据和平滑后的数据
plot(1:100, data, 'o', 1:0.1:100, data_smooth, '-');
legend('原始数据', '平滑后的数据');

**逻辑分析：**

* 线性插值将相邻数据点连接起来，形成一条平滑曲线。
* 平滑后的数据 `data_smooth` 中，噪声和毛刺已被去除，数据变得更加平滑。

#### 4.2.2 线性插值用于数据降噪

数据降噪是指去除数据中的噪声，使数据更干净。线性插值可以用来降噪，通过将相邻数据点取平均值来代替原始数据。

**代码示例：**

% 生成带有噪声的数据
data = randn(100, 1) + 0.5 * sin(1:100);

% 使用线性插值降噪
data_denoise = interp1(1:100, data, 1:0.5:100, 'linear');

% 绘制原始数据和降噪后的数据
plot(1:100, data, 'o', 1:0.5:100, data_denoise, '-');
legend('原始数据', '降噪后的数据');

**逻辑分析：**

* 线性插值将相邻数据点取平均值，形成一条平滑曲线。
* 降噪后的数据 `data_denoise` 中，噪声已被去除，数据变得更加干净。

# 5.1 多维线性插值

### 5.1.1 多维线性插值的原理和实现

多维线性插值是线性插值的推广，用于对多维数据进行插值。其原理与一维线性插值类似，都是通过构建一个多维超平面来近似原始数据。

假设我们有一个定义在多维空间上的函数 $f(x_1, x_2, \cdots, x_n)$，其中 $x_i$ 是第 $i$ 维的变量。多维线性插值的目标是根据已知数据点 $(x_1^i, x_2^i, \cdots, x_n^i, f^i)$，估计未知点 $(x_1, x_2, \cdots, x_n)$ 处的函数值 $f(x_1, x_2, \cdots, x_n)$。

多维线性插值的基本思想是：对于未知点 $(x_1, x_2, \cdots, x_n)$，首先在每个维度上进行一维线性插值，得到 $n$ 个插值值 $f_i(x_i)$。然后，将这些插值值线性组合起来，得到多维线性插值结果：

$$f(x_1, x_2, \cdots, x_n) \approx \sum_{i=1}^n w_i f_i(x_i)$$

其中 $w_i$ 是权重系数，由各个维度上的一维线性插值权重计算得到。

### 5.1.2 多维线性插值在图像处理中的应用

多维线性插值在图像处理中有着广泛的应用，例如图像缩放、旋转和透视变换。

在图像缩放中，多维线性插值可以用于将图像放大或缩小。放大时，需要在原图像中插入新的像素点，而缩小时需要删除一些像素点。多维线性插值通过对图像的每个像素点进行多维线性插值，得到新图像中对应像素点的颜色值。

在图像旋转和透视变换中，多维线性插值可以用于将图像旋转或变换到任意角度。这需要对图像中的每个像素点进行多维线性插值，得到变换后图像中对应像素点的颜色值。

% 读取图像
img = imread('image.jpg');

% 图像缩放
scale = 2;
new_img = imresize(img, scale, 'bilinear');

% 图像旋转
angle = 30;
rotated_img = imrotate(img, angle, 'bilinear');

% 图像透视变换
tform = maketform('projective', [1 0 0; 0 1 0; 0.1 0.1 1]);
transformed_img = imtransform(img, tform, 'bilinear');

# 6. MATLAB线性插值总结与展望

### 6.1 线性插值在数据分析中的重要性

线性插值作为一种简单而有效的插值技术，在数据分析中发挥着至关重要的作用。它可以有效解决缺失数据、数据平滑和降噪等问题，为数据分析提供可靠的基础。

在实际应用中，线性插值广泛应用于以下领域：

- **时间序列分析：** 用于预测未来趋势和填补缺失数据。
- **图像处理：** 用于图像缩放、旋转和透视变换。
- **科学计算：** 用于求解偏微分方程和模拟复杂物理现象。

### 6.2 线性插值的发展趋势和未来展望

随着数据分析技术的不断发展，线性插值也在不断演进和完善。以下是一些值得关注的发展趋势：

- **高维线性插值：** 扩展线性插值到更高维度，以处理复杂的多维数据。
- **自适应线性插值：** 根据数据分布动态调整插值参数，提高插值精度。
- **机器学习辅助线性插值：** 利用机器学习算法优化插值过程，提升插值性能。

未来，线性插值有望在以下方面取得进一步突破：

- **实时数据插值：** 实现对大规模实时数据的快速插值，满足工业物联网和自动驾驶等应用场景的需求。
- **非线性插值：** 探索非线性插值技术，以提高对复杂数据的插值精度。
- **多源数据插值：** 融合来自不同来源的数据，进行更加准确和鲁棒的插值。