【树排序算法】：二叉树与排序的不解之缘，打造高性能算法

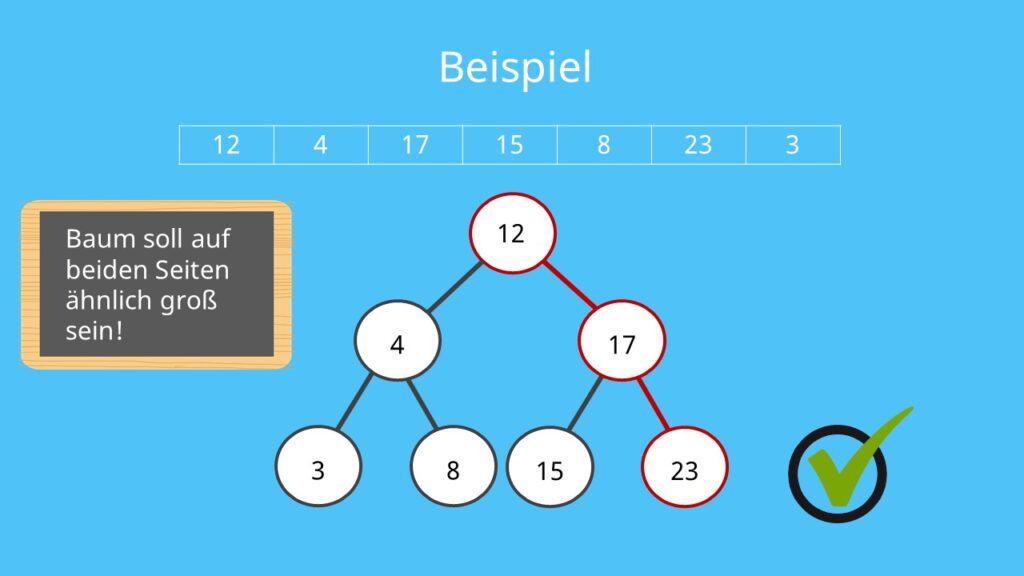
# 1. 树排序算法概述

树排序算法是一类通过构造树形数据结构来实现排序的方法，其中最典型的代表是基于二叉搜索树（BST）的排序。在树排序中，元素被插入到树中的合适位置，然后根据树的遍历顺序输出来完成排序任务。这种排序方式在算法的稳定性和排序效率上有其独特的优势，尤其适合在大量数据排序中保持数据的组织结构，以实现更快的检索和插入操作。随着树结构的不断优化，如平衡二叉树（AVL树）和红黑树等，树排序算法的性能得到了显著的提升，成为了研究和应用的热点。在本文中，我们将从二叉树的基础知识入手，逐步深入探讨树排序算法的原理、实现、优化策略以及其在未来排序技术中的潜力。

# 2. 二叉树基础与性质

## 2.1 二叉树的定义与类型

### 2.1.1 二叉树的概念与特点

在计算机科学中，二叉树是一种重要且常用的树形数据结构，具有如下特点：

- 每个节点最多有两个子节点：一个左子节点和一个右子节点。
- 二叉树的节点层级结构可以用于描述元素之间的层级关系。
- 二叉树的子树也有其自己的顺序，即左子树和右子树是区分的，它们在结构上可以视为独立的二叉树。

二叉树之所以受到重视，是因为它在数据组织和检索方面提供了便利，尤其是二叉搜索树（BST），由于其高效的操作性能，被广泛应用于各种排序和搜索算法中。

### 2.1.2 完全二叉树与满二叉树

根据节点的填充情况，二叉树可以分为完全二叉树和满二叉树：

- **满二叉树**：每一层的节点数量都是满的，即除了叶子节点外，每个节点都有两个子节点。
- **完全二叉树**：从上至下，从左到右依次填充节点，可能最底层未完全填充，但节点填充是连续的。

满二叉树是完全二叉树的特例。完全二叉树在数组实现上有优势，因为可以无需指针直接计算子节点位置。

## 2.2 二叉树的遍历算法

### 2.2.1 前序、中序与后序遍历

二叉树的遍历是按照节点的访问顺序来定义的：

- **前序遍历**：首先访问根节点，然后遍历左子树，最后遍历右子树。
- **中序遍历**：首先遍历左子树，然后访问根节点，最后遍历右子树。
- **后序遍历**：首先遍历左子树，然后遍历右子树，最后访问根节点。

中序遍历特别重要，因为它对于二叉搜索树来说可以得到有序序列。以下是中序遍历的伪代码实现：

def inorder_traversal(root):
    if root is not None:
        inorder_traversal(root.left)
        print(root.value)
        inorder_traversal(root.right)

### 2.2.2 层次遍历及其算法实现

层次遍历是指按照从上到下，从左到右的顺序访问二叉树的每一层：

- 使用队列来进行层次遍历，先将根节点入队，然后循环执行以下操作：
- 节点出队，访问该节点。
- 如果该节点有左子节点，左子节点入队。
- 如果该节点有右子节点，右子节点入队。

以下是层次遍历的伪代码实现：

from collections import deque

def level_order_traversal(root):
    if root is None:
        return
    queue = deque([root])
    while queue:
        node = queue.popleft()
        print(node.value)
        if node.left:
            queue.append(node.left)
        if node.right:
            queue.append(node.right)

层次遍历的结果反映了二叉树的结构层次，常用在树的深度和广度相关问题中。

## 2.3 二叉搜索树（BST）

### 2.3.1 二叉搜索树的特性

二叉搜索树（BST）是一种特殊的二叉树，它满足以下性质：

- 对于树中的每个节点X，它的左子树中所有项的值小于X的值。
- 对于树中的每个节点X，它的右子树中所有项的值大于X的值。
- 左、右子树也分别为二叉搜索树。

由于这种性质，BST支持快速查找、插入和删除操作。BST在二叉树的基础上，保证了树的平衡性，为高效数据访问提供了基础。

### 2.3.2 插入、删除操作的实现

插入操作比较简单，根据BST的性质，可以按照以下步骤进行：

1. 从根节点开始，比较插入的值与当前节点值的大小。
2. 如果插入的值较小，则向左子树移动，否则向右子树移动。
3. 重复这个过程，直到找到一个空的子节点，将新节点插入其中。

以下是插入操作的伪代码：

class TreeNode:
    def __init__(self, key):
        self.left = None
        self.right = None
        self.val = key

def insert(root, key):
    if root is None:
        return TreeNode(key)
    else:
        if root.val < key:
            root.right = insert(root.right, key)
        else:
            root.left = insert(root.left, key)
    return root

删除操作更为复杂，因为需要考虑删除节点的不同情况：

1. **删除叶节点**：直接删除即可。
2. **删除有一个子节点的节点**：用其子节点替代其位置。
3. **删除有两个子节点的节点**：通常用右子树的最小值或左子树的最大值节点来替换被删除的节点，然后删除这个替代节点。

以下是删除操作的伪代码实现：

def delete_node(root, key):
    if root is None:
        return root
    if key < root.val:
        root.left = delete_node(root.left, key)
    elif key > root.val:
        root.right = delete_node(root.right, key)
    else:
        if root.left is None:
            temp = root.right
            root = None
            return temp
        elif root.right is None:
            temp = root.left
            root = None
            return temp
        temp = minValueNode(root.right)
        root.val = temp.val
        root.right = delete_node(root.right, temp.val)
    return root

def minValueNode(