Java搜索算法优化：BFS与DFS的实现及性能提升策略


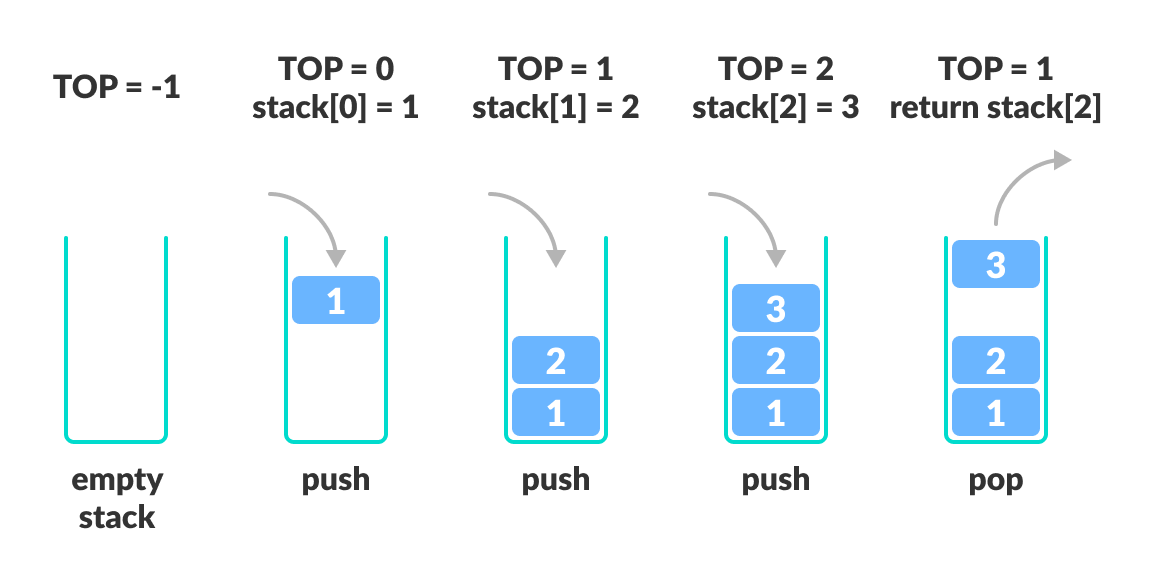
# 摘要
搜索算法是计算机科学中的基础组成部分，在解决各种复杂问题中发挥关键作用。本文首先介绍了搜索算法的基础知识以及Java实现方式，接着深入探讨了广度优先搜索（BFS）和深度优先搜索（DFS）的原理、应用实例及Java代码实现。文章进一步分析了BFS与DFS在性能上的差异，并探讨了如何优化这些算法。此外，本文还研究了搜索算法优化的实践，包括数据结构优化、多线程应用以及在大数据环境下的挑战和解决方案。最后，文章展望了搜索算法的未来趋势，包括应对高维度数据和非确定性问题的策略，以及量子计算和机器学习等前沿技术的潜在影响和应用前景。

# 关键字
搜索算法；Java实现；BFS；DFS；性能优化；大数据；量子计算；机器学习；高维度数据；非确定性问题

参考资源链接：[Java数据结构与算法实战：从基础知识到高级应用](https://wenku.csdn.net/doc/644b7d67fcc5391368e5ee95?spm=1055.2635.3001.10343)
# 1. 搜索算法基础与Java实现

搜索算法是计算机科学中的一个基础分支，它广泛应用于数据结构、人工智能、网络通信等领域。掌握搜索算法是解决复杂问题的关键。在这一章中，我们将从搜索算法的基本概念开始，逐步深入至其在Java中的实现方法。首先，我们会介绍搜索算法的类型，特别是常见的广度优先搜索（BFS）和深度优先搜索（DFS）；然后，我们会探讨这些算法在解决问题时的效率以及它们的适用场景。在此基础上，我们将会展示如何使用Java语言实现这些算法，并通过实例演示它们的应用。

接下来，让我们开始了解搜索算法的一些基本概念和原理。

# 2. 广度优先搜索（BFS）的原理与应用

广度优先搜索（BFS）是图搜索算法中最基本的算法之一，以一种逐层的方式探索图的所有节点。在这一章中，我们将探讨BFS的基本原理，它的在树和图结构中的应用实例，以及通过Java实现的具体细节。

## 2.1 BFS基本概念与算法流程

### 2.1.1 树与图的遍历基础

在数据结构中，树是一种常见的结构，可以用来表示具有层级关系的数据。树的遍历算法是理解BFS的重要基础。BFS遍历树时，可以按层次从上到下、从左到右的顺序访问每一个节点。图作为一种更加复杂的结构，可以包含循环和多对多的关系。图的遍历有深度优先遍历（DFS）和广度优先遍历（BFS），其中BFS能够保证以最小的步数访问所有与起始点相连的节点。

### 2.1.2 BFS算法的队列实现原理

BFS算法的核心思想是使用队列来存储每一层的节点，并在访问完当前层的节点后，将它们的未访问的邻接点加入队列中。这个过程重复进行，直到队列为空。在Java中，可以使用`LinkedList`来实现队列的操作。每访问一个节点，将其标记为已访问，并将其邻接点入队。这样，算法保证了每层节点的遍历，从而达到广度优先的目的。

## 2.2 BFS在树和图结构中的应用实例

### 2.2.1 解决迷宫问题的BFS实现

在解决迷宫问题时，我们可以将迷宫看作是一个图，其中每个房间是一个节点，相邻的房间之间有一条边。BFS算法可以用来找到从起点到终点的最短路径。算法从起点开始，访问所有相邻的未访问节点，并将这些节点的相邻节点入队。重复此过程，直到找到终点或者队列为空。

import java.util.LinkedList;
import java.util.Queue;

public class MazeSolver {
    public static boolean solveMaze(int[][] maze, int startRow, int startCol, int endRow, int endCol) {
        boolean[][] visited = new boolean[maze.length][maze[0].length];
        Queue<Point> queue = new LinkedList<>();

        // 定义四个方向的移动
        int[][] dirs = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
        queue.add(new Point(startRow, startCol));
        visited[startRow][startCol] = true;

        while (!queue.isEmpty()) {
            Point current = queue.poll();
            if (current.row == endRow && current.col == endCol) {
                return true;
            }

            for (int[] dir : dirs) {
                int newRow = current.row + dir[0];
                int newCol = current.col + dir[1];

                // 检查新位置是否在迷宫内，是否为通道以及是否未访问
                if (isSafe(maze, newRow, newCol, visited)) {
                    queue.add(new Point(newRow, newCol));
                    visited[newRow][newCol] = true;
                }
            }
        }
        return false;
    }

    private static boolean isSafe(int[][] maze, int row, int col, boolean[][] visited) {
        return (row >= 0 && row < maze.length && col >= 0 && col < maze[0].length && 
                maze[row][col] == 1 && !visited[row][col]);
    }

    public static void main(String[] args) {
        int[][] maze = {
            {1, 0, 0, 0},
            {1, 1, 0, 1},
            {0, 1, 0, 0},
            {1, 1, 1, 1}
        };

        int startRow = 0, startCol = 0;
        int endRow = 3, endCol = 3;

        boolean result = solveMaze(maze, startRow, startCol, endRow, endCol);
        System.out.println("Can the exit be reached? " + result);
    }
}

class Point {
    int row, col;

    public Point(int row, int col) {
        this.row = row;
        this.col = col;
    }
}

### 2.2.2 网络爬虫中的BFS策略

在构建网络爬虫时，BFS可以用来按照网页链接的层次结构进行网页的抓取。从种子URL开始，使用BFS遍历网页链接，每次抓取一个网页，再将其链接的网页加入队列中。这样可以保持页面抓取的顺序性和广度，避免过早地深入某一子域而忽略了其他重要链接。

## 2.3 BFS的Java代码实现

### 2.3.1 Java集合框架中的队列使用

Java的集合框架中提供了多种队列实现，其中`LinkedList`实现了`Queue`接口，适用于BFS算法中作为节点存储结构。在BFS中，我们主要使用队列的`add`、`poll`和`isEmpty`方法。

### 2.3.2 BFS算法的核心Java代码

以下是使用Java实现BFS算法的核心代码，用于演示如何对图结构进行遍历。

import java.util.LinkedList;
import java.util.Queue;

public class GraphBFS {
    private int vertices; // 图的节点数
    private LinkedList<Integer>[] adj; // 邻接表表示图

    // 构造函数
    public GraphBFS(int vertices) {
        this.vertices = vertices;
        adj = new LinkedList[vertices];
        for (int i = 0; i < vertices; i++) {
            adj[i] = new LinkedList<>();
        }
    }

    // 添加边
    public void addEdge(int src, int dest) {
        adj[src].add(dest); // 添加一条从src到dest的边
    }

    // BFS算法实现
    public void bfs(int startVertex) {
        boolean[] visited = new boolean[vertices];
        Queue<Integer> queue = new LinkedList<>();

        visited[startVertex] = true;
        queue.add(startVertex);

        while (!queue.isEmpty()) {
            int currVertex = queue.poll();
            System.out.print(currVertex + " ");

            for (int adjVertex : adj[currVertex]) {
                if (!visited[adjVertex]) {
                    visited[adjVertex] = true;
                    queue.add(adjVertex);
                }
            }
        }
    }

    public static void main(String[] args) {
        GraphBFS graph = new GraphBFS(4);
        graph.addEdge(0, 1);
        graph.addEdge(0, 2);
        graph.addEdge(1, 2);
        graph.addEdge(2, 0);
        graph.addEdge(2, 3);
        graph.addEdge(3, 3);

        System.out.println("Following is Breadth First Traversal starting from vertex 2:");
        graph.bfs(2);
    }
}

这段代码展示了如何通过Java实现一个简单图的广度优先搜索。通过邻接表存储图结构，并通过队列实现BFS搜索过程，从而遍历图中所有可达的节点。

# 3. 深度优先搜索（DFS）的原理与应用

深度优先搜索（DFS）是一种用于遍历或搜索树或图的算法。在树中，该算法从根节点开始，沿着树的分支进行深度探索，直到找到目标节点或达到叶子节点为止。在图中，DFS同样按照这一策略进行，但在实现时需要额外考虑避免陷入环路中。本章将详细介绍DFS的原理，探索其在不同数据结构中的应用，并提供Java语言的实现示例。

## 3.1 DFS基本概念与算法流程

### 3.1.1 DFS的递归逻辑分析

深度优先搜索的核心在于递归调用，通过递归的方式，算法可以深入到