振动分析在制造业中的价值：提升产品质量，降低成本，助力企业发展

# 1. 振动分析概述

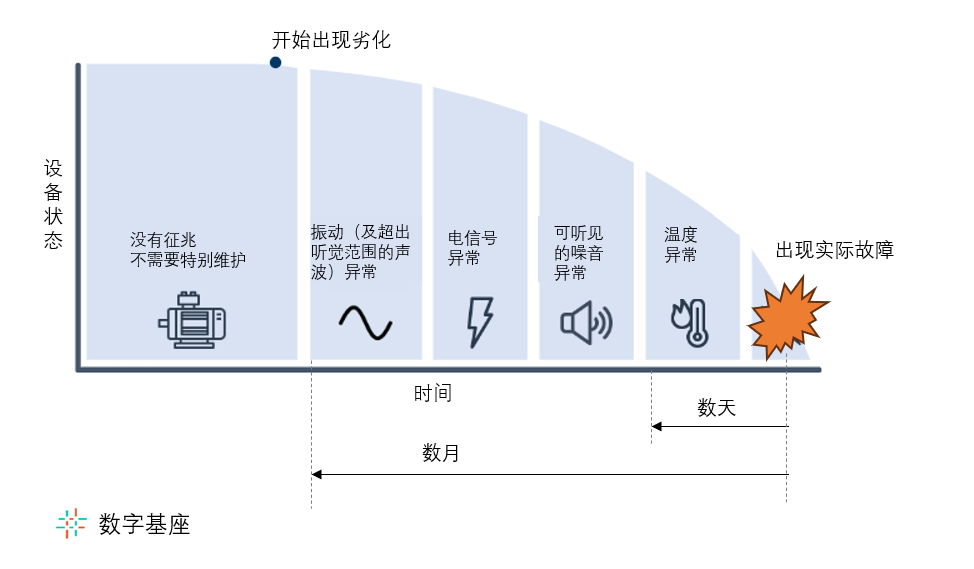
振动分析是一门研究物体振动特性和规律的学科，广泛应用于制造业、航空航天、土木工程等领域。其核心原理是通过测量和分析物体的振动信号，获取其动力学特性、故障信息和健康状态等信息。

振动分析具有非接触、无损检测的特点，可以实时监测和诊断设备的运行状况，及时发现潜在故障隐患，避免重大安全事故的发生。通过振动分析，工程师可以优化产品设计、提高生产效率、降低成本，从而助力企业发展。

# 2. 振动分析原理和技术

### 2.1 振动理论基础

#### 2.1.1 振动定义和类型

**定义：**振动是指物体相对于其平衡位置的往复运动，通常由周期性的力或扰动引起。

**类型：**

- **自由振动：**物体在受到一次扰动后，在没有外力作用下自行振动。
- **受迫振动：**物体在周期性外力的作用下振动。
- **阻尼振动：**物体在振动过程中受到阻力或摩擦力，导致振幅逐渐减小。
- **共振：**当外力频率与物体的固有频率相同时，振幅会显著增大。

#### 2.1.2 振动测量原理

振动测量通常使用加速度传感器或位移传感器。

**加速度传感器：**

- 测量物体相对于惯性参考系的加速度。
- 单位：米/秒²（m/s²）。
- 优点：灵敏度高，不受重力影响。

**位移传感器：**

- 测量物体相对于固定参考点的位移。
- 单位：米（m）。
- 优点：精度高，可直接测量振幅。

### 2.2 振动分析技术

振动分析技术主要分为时域分析、频域分析和模态分析。

#### 2.2.1 时域分析

**原理：**直接观察振动信号在时间域中的变化。

**应用：**

- 检测振动幅度和频率。
- 识别冲击、脉冲等瞬态事件。
- 评估振动对设备或结构的影响。

**代码示例：**

import numpy as np
import matplotlib.pyplot as plt

# 生成正弦波信号
t = np.linspace(0, 1, 1000)
y = np.sin(2 * np.pi * 10 * t)

# 绘制时域图
plt.plot(t, y)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.show()

**逻辑分析：**

- `np.linspace(0, 1, 1000)` 生成 1000 个从 0 到 1 的时间点。
- `np.sin(2 * np.pi * 10 * t)` 生成频率为 10 Hz 的正弦波信号。
- `plt.plot(t, y)` 绘制时域图，横轴为时间，纵轴为振幅。

#### 2.2.2 频域分析

**原理：**将时域信号转换为频域信号，分析不同频率成分的幅度和相位。

**应用：**

- 识别振动源和故障频率。
- 评估共振和阻尼特性。
- 进行故障诊断和预测。

**代码示例：**

import numpy as np
from scipy.fftpack import fft

# 生成正弦波信号
t = np.linspace(0, 1, 1000)
y = np.sin(2 * np.pi * 10 * t)

# 进行傅里叶变换
Y = fft(y)

# 计算频率和幅度
freq = np.fft.fftfreq(len(y), t[1] - t[0])
amplitude = 2 * np.abs(Y) / len(y)

# 绘制频域图
plt.plot(freq, amplitude)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.show()

**逻辑分析：**

- `np.fft.fftfreq(len(y), t[1] - t[0])` 计算频率。
- `2 * np.abs(Y) / len(y)` 计算幅度。
- `plt.plot(freq, amplitude)` 绘制频域图，横轴为频率，纵轴为幅度。

#### 2.2.3 模态分析

**原理：**通过激振和响应测量，确定结构或设备的固有频率、阻尼比和模态形状。

**应用：**

- 评估结构的动力特性。
- 识别共振频率和模态形状。
- 进行故障诊断和预测。

**流程图：**

graph LR
subgraph 模态分析流程
    A[激振] --> B[响应测量] --> C[数据处理] --> D[模态参数识别]
end

**参数说明：**

- 激振：施加在结构或设备上的力或扰动。
- 响应测量：测量结构或设备在激振下的振动响应。
- 数据处理：对响应数据进行预处理、特征提取和信号处理。
- 模态参数识别：利用数学算法，从处理后的数据中识别固有频率、阻尼比和模态形状。

# 3.1 产品质量控制

振动分析在产品质量控制中发挥着至关重要的作用，它通过检测和分析产品在不同工况下的振动特性，帮助企业识别和解决潜在的质量问题。

#### 3.1.1 振动分析在产品设计中的应用

在产品设计阶段，振