【掌握线性代数：基础到应用的全面解读】：彻底理解《线性代数介绍》第五版，开启数学与实际问题的桥梁


参考资源链接：[线性代数第五版习题解答手册——Gilbert Strang](https://wenku.csdn.net/doc/6401abf3cce7214c316ea169?spm=1055.2635.3001.10343)
# 1. 线性代数基础知识

在开始深入线性代数的广阔领域之前，先了解一些核心的基础概念和原理是至关重要的。这将帮助我们打下坚实的基础，为后续章节中探讨更高级的主题做好准备。

## 1.1 线性代数概述
线性代数是数学的一个分支，专注于向量空间（亦称线性空间）、线性映射（线性变换）以及这两个概念的最基本元素——向量和矩阵。它是现代数学的基石之一，在多个学科领域中都扮演着核心角色，包括物理学、计算机科学、工程技术、经济学，以及许多其他的应用科学领域。

## 1.2 向量及其运算
在数学和物理学中，向量是具有大小和方向的量。在几何上，可以将向量视为点到点的位移。向量的加法和数乘是两种基本运算，它们满足八条运算律，构成向量空间的基础。了解如何操作向量对于掌握线性代数至关重要，因为向量运算不仅仅局限于简单的代数运算，还包括向量点乘和叉乘等更高级的运算。

## 1.3 系统方程与解的结构
线性代数中，线性方程组通常表示为Ax = b的形式，其中A是系数矩阵，x是未知向量，b是常数向量。系统方程的解可以是无解、唯一解或无穷多解，这取决于系数矩阵A的特性。解决这些问题的关键在于理解矩阵的秩、零空间、列空间等概念，这些概念在后续章节中将详细探讨。掌握线性方程组的解法对于理解和应用线性代数至关重要。

# 2. 向量空间与线性变换

向量空间和线性变换是线性代数中核心的概念之一，它们为处理线性问题提供了丰富的理论基础和强大的工具。在这一章节中，我们将探索向量空间的基本概念，理解其性质，以及如何通过线性变换在不同的向量空间中进行映射。

### 2.1 向量空间的定义与性质

向量空间是由向量组成的集合，它在加法和数乘运算下是封闭的。向量空间的定义为数学和工程问题提供了一个具有丰富结构的框架。

#### 2.1.1 子空间的构造与判定

子空间是向量空间的一个特殊情况，它自身也是向量空间。子空间的存在需要满足以下条件：

- 非空：子空间至少包含零向量。
- 封闭性：对于子空间中的任何两个向量，其线性组合仍然属于该子空间。

判定一个子空间的一个常见方法是通过检查一组向量的生成集。例如，考虑在实数域上的向量空间，任取一组向量 \( \{v_1, v_2, ..., v_k\} \)，所有可能的线性组合构成的集合 \( V \) 是一个子空间。

#### 2.1.2 基与维数的概念

基是向量空间的一个重要概念，它是指由一组线性无关向量组成的集合。基中的向量能够生成整个空间，即向量空间中的任何向量都可以通过这组基向量的线性组合唯一表示。维数是基的大小，即基中向量的数量。例如，三维空间的基由三个线性无关的向量组成，因此其维数为3。

### 2.2 线性变换及其矩阵表示

#### 2.2.1 线性变换的定义和例子

线性变换是保持加法和标量乘法操作的函数。换言之，对于向量空间 \(V\) 和 \(W\) 之间的线性变换 \(T: V \rightarrow W\)，需满足以下性质：

- \(T(u + v) = T(u) + T(v)\) (加法保持)
- \(T(cv) = cT(v)\) (标量乘法保持)

其中 \(u, v\) 是 \(V\) 中的向量，\(c\) 是标量。一个简单的例子是二维空间的旋转变换，它将每个向量按固定角度旋转。

#### 2.2.2 核与像的概念及其计算

核（Kernel）是线性变换中一个特别重要的概念，它包括所有被变换到零向量的原向量。数学上，核可以表示为 \( \text{Ker}(T) = \{ v \in V : T(v) = 0\} \)。

像（Image）指的是线性变换后向量空间的子集，包含所有由原空间向量通过线性变换所获得的向量。如果 \(T: V \rightarrow W\)，则像 \( \text{Im}(T) \) 是 \(W\) 的子集，定义为 \( \text{Im}(T) = \{ w \in W : w = T(v) \text{ for some } v \in V \} \)。

#### 2.2.3 变换的复合与矩阵乘法

两个线性变换的复合仍然是一个线性变换。对于线性变换 \(T_1: V \rightarrow W\) 和 \(T_2: W \rightarrow U\)，复合变换 \(T_2 \circ T_1\) 表示先应用 \(T_1\) 再应用 \(T_2\)。

在矩阵表示中，线性变换 \(T: V \rightarrow W\) 可以通过矩阵乘法来实现。如果有基 \( \{v_1, v_2, ..., v_n\} \) 和 \( \{w_1, w_2, ..., w_m\} \) 分别定义在 \(V\) 和 \(W\) 中，那么变换 \(T\) 可以用一个 \(m \times n\) 的矩阵表示，该矩阵的列向量是 \(T(v_i)\) 以 \(w\) 的基表示的系数。

#### 代码块展示

import numpy as np

# 示例：实现一个线性变换的矩阵乘法
# 定义变换矩阵 A
A = np.array([[1, 2], [3, 4]])

# 定义向量 v
v = np.array([5, 6])

# 计算线性变换后的向量 Av
Av = np.dot(A, v)

print("变换矩阵 A:")
print(A)
print("原始向量 v:")
print(v)
print("线性变换 Av:")
print(Av)

以上代码演示了如何通过矩阵乘法实现线性变换，矩阵 A 与向量 v 的点乘将产生一个新的向量 Av，这个向量代表了原始向量经过线性变换后在目标空间中的位置。

# 以下是对线性变换核和像的代码演示
# 假设我们有一个线性变换 T，用矩阵 A 表示
# 我们将计算这个变换的核和像

from scipy.linalg import null_space

# 计算核
null_A = null_space(A)
print("变换 A 的核:")
print(null_A)

# 计算像
# 假设我们通过 A 的列向量生成向量空间 W
W = np.array([A[:, 0], A[:, 1]]).T

# 计算 W 的子空间的基
basis_W = null_space(W)
print("变换 A 的像:")
print(basis_W)

在这个代码块中，我们演示了如何计算线性变换的核和像。使用 SciPy 库中的 `null_space` 函数可以计算一个矩阵的核，而通过计算像空间的一组基，我们能够推断出线性变换的像。

通过本章的内容，我们将深入理解向量空间和线性变换的理论基础，为线性代数的深入学习打下坚实的基础，并且探索如何将这些理论应用到实际问题中去。

# 3. 矩阵理论及其应用

## 3.1 矩阵的基本概念与分类
### 3.1.1 矩阵的运算规则

矩阵是线性代数中的核心概念，其运算规则是矩阵理论的基础。矩阵的运算主要包括加法、减法、数乘、乘法以及转置等。在分析这些运算时，我们通常关注它们的性质，比如交换律、结合律以及分配律是否成立。

例如，对于矩阵的加法运算，给定两个相同大小的矩阵A和B，它们的和C定义为C的每个元素等于A和B对应位置元素的和。具体来说，如果矩阵A和B都是m×n的，那么它们的和C同样是一个m×n的矩阵，其(i, j)元素c_ij = a_ij + b_ij，其中i代表行索引，j代表列索引。

矩阵乘法相比加法要复杂一些，要求第一个矩阵的列数与第二个矩阵的行数相等。假设矩阵A的维度是m×n，矩阵B的维度是n×p，那么乘积C将是一个m×p的矩阵，C中的每个元素是通过对A的行和B的列进行内积运算得到的。

值得注意的是，矩阵乘法不满足交换律，也就是说AB不一定等于BA，即便这两个乘积都存在。

| A |     | B |     | C = AB |
|---|  *  |---|  =  |--------|
| a11 a12 | * | b11 b12 | c11 c12 |
| a21 a22 |   | b21 b22 | c21 c22 |

在上表中，矩阵C的每个元素c_ij是通过将矩阵A的第i行与矩阵B的第j列进行内积得到的。这种运算规则是计算矩阵乘法的基础。

### 3.1.2 特殊矩阵的性质与应用

在矩阵的世界里，特殊矩阵拥有许多有趣的性质，它们在实际应用中扮演着关键角色。这些特殊矩阵包括对角矩阵、单位矩阵、稀疏矩阵、对称矩阵以及正交矩阵等。

- **对角矩阵**：对角线以外的元素都为零的矩阵。对角矩阵的乘法运算非常方便，仅需对角线元素相乘即可。
- **单位矩阵**：所有对角线元素都是1的对角矩阵，乘法运算下任何矩阵和单位矩阵的乘积等于原矩阵。
- **稀疏矩阵**：大部分元素为零的矩阵。在存储和计算上可以大大简化。
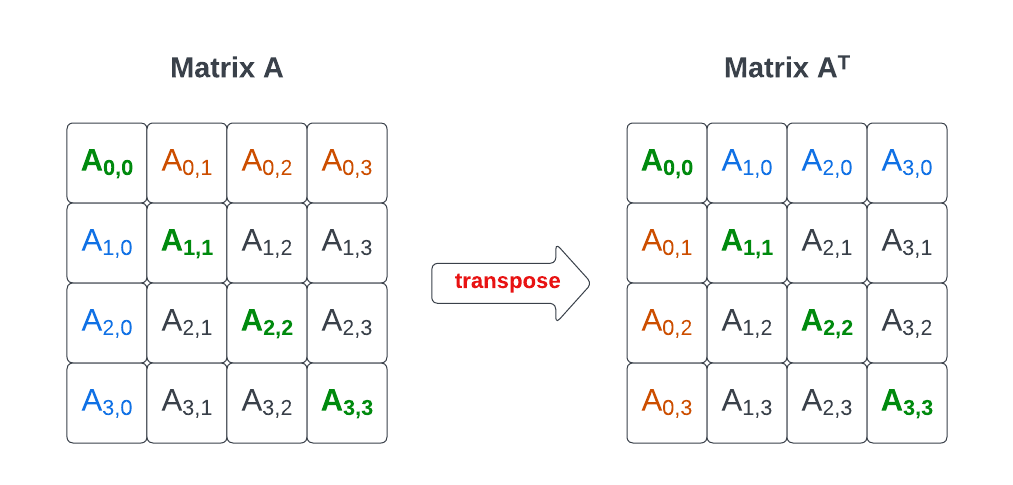
- **对称矩阵**：满足A = A^T的矩阵，即矩阵关于其主对角线对称。对称矩阵在物理、工程学和经济学中有重要应用。
- **正交矩阵**：满足Q^TQ = QQ^T = I的矩阵，其中Q^T是Q的转置，I是单位矩阵。正交矩阵在表示旋转或变换中非常有用。

这些特殊矩阵的性质，不仅为理论分析提供便利，还使得在实际计算中能够降低复杂度，提高效率。例如，在图像处理、量子计算以及机器学习算法中，使用特殊矩阵可以显著减少计算资源的消耗。

| 矩阵类型 | 定义 | 应用 |
|----------|------|------|
| 对角矩阵 | 主对角线以外的元素为零 | 方便乘法运算 |
| 单位矩阵 | 所有对角线元素为1的对角矩阵 | 身份变换 |
| 稀疏矩阵 | 大部分元素为零 | 降低存储和计算资源 |
| 对称矩阵 | A = A^T | 物理学、工程学和经济学 |
| 正交矩阵 | Q^TQ = I | 表示旋转或正交变换 |

在接下来的章节中，我们将深入探讨矩阵理论中的行列式与矩阵的逆，以及线性方程组的解法，这些内容将帮助我们更好地理解和运用矩阵。

# 4. 特征值问题与对角化

## 4.1 特征值与特征向量

### 4.1.1 特征值问题的定义与求解

在数学中，一个n×n的方阵A与一个非零n维列向量v和标量λ之间的关系，可以由以下方程定义：

\[ A \cdot v = \lambda \cdot v \]

这里的λ称为矩阵A的一个特征值，对应的v称为属于特征值λ的特征向量。特征值和特征向量在多个领域中都非常重要，例如在工程学、物理学、计算机科学等领域。求解特征值的过程通常涉及到求解多项式方程，这个方程的根就是特征值。具体步骤如下：

1. 首先，构造特征多项式：将特征值问题转化为求解行列式的问题。对于矩阵A，构造行列式 |A - λI| = 0，其中I是单位矩阵。
2. 解这个n次方程，找到所有的λ值，这些值就是矩阵A的特征值。
3. 对每个特征值λ，解齐次线性方程组 (A - λI) \cdot v = 0，找到对应的非零解v，即为特征向量。

#### 示例代码

假设有一个矩阵A：

import numpy as np

A = np.array([[4, 2], [1, 3]])

计算其特征值和特征向量：

eigenvalues, eigenvectors = np.linalg.eig(A)

这段代码将返回A的特征值和对应的特征向量矩阵，其中`eigenvalues`包含了特征值，`eigenvectors`的每一列则对应于一个特征值的特征向量。

#### 参数说明

- `A`: 要求特征值和特征向量的矩阵。
- `np.linalg.eig`: NumPy库中的函数，用于计算方阵的特征值和特征向量。

### 4.1.2 特征向量的性质及其应用

特征向量具有以下几个重要性质：

- 特征向量的方向在矩阵作用下保持不变，只是长度可能发生变化。
- 对于非退化矩阵，每个特征值都对应至少一个特征向量。
- 不同特征值对应的特征向量线性无关。

特征向量在物理、工程、计算机科学等领域有着广泛的应用，比如：

- 在量子力学中，粒子的状态可以用特征向量表示。
- 在图像处理中，特征向量可以用来表示图像的特征。
- 在数据压缩中，特征向量可以用来定义数据的主成分。

#### 示例代码

使用特征向量进行数据压缩：

# 假设U是特征向量组成的矩阵，X是原始数据矩阵
reduced_data = np.dot(X, U[:, :k])

这段代码使用前k个特征向量对原始数据进行降维处理，`k`是选定的特征数量。

#### 参数说明

- `U[:, :k]`: U矩阵的前k列，代表了前k个最重要的特征向量。
- `X`: 原始数据矩阵，每一行代表一个数据点。
- `np.dot`: NumPy库中的矩阵乘法函数，用于降维压缩。

### 4.2 对角化及其几何意义

#### 4.2.1 对角化的条件与过程

一个方阵A可以通过相似变换对角化的条件是：

- 矩阵A有n个线性无关的特征向量。

对角化的步骤如下：

1. 找到矩阵A的所有特征值。
2. 对每个特征值，找到对应的特征向量。
3. 将这些特征向量作为列向量组成一个矩阵P。
4. 计算对角矩阵D = P⁻¹AP。

#### 示例代码

P = eigenvectors  # 特征向量矩阵
D = np.diag(eigenvalues)  # 对角矩阵

A_diag = np.dot(np.dot(P, D), np.linalg.inv(P))

这段代码首先构造特征向量矩阵P和对角矩阵D，然后计算对角化后的矩阵A_diag。

#### 参数说明

- `eigenvectors`: 包含所有特征向量的矩阵。
- `eigenvalues`: 包含对应特征值的数组。
- `np.diag`: NumPy库中的函数，用于生成对角矩阵。
- `np.linalg.inv`: 计算矩阵的逆。

#### 4.2.2 对角化在变换中的作用

对角化可以简化线性变换的计算。如果一个矩阵能够对角化，那么对角矩阵D代表了线性变换在特定基下的表示。在这个基下，线性变换可以通过简单的缩放来实现，这比原始矩阵的乘法要简单得多。

### 4.3 正定矩阵与二次型

#### 4.3.1 正定矩阵的判定方法

正定矩阵是具有特殊性质的实对称矩阵，其所有的特征值都是正的。判定一个矩阵是否为正定矩阵的方法有多种：

- 所有的顺序主子式（leading principal minors）都是正的。
- 矩阵的所有特征值都是正数。

#### 示例代码

from numpy.linalg import cholesky

def is_positive_definite(A):
    try:
        L = cholesky(A)
        return True
    except np.linalg.LinAlgError:
        return False

这段代码利用Cholesky分解来判定矩阵是否为正定。如果分解成功，则矩阵是正定的。

#### 参数说明

- `cholesky`: NumPy库中的函数，用于进行Cholesky分解。
- `A`: 需要进行判定的矩阵。

#### 4.3.2 二次型的标准形与简化

二次型可以通过正交变换转化为标准形，其过程与对角化类似。给定一个实数二次型，我们可以通过坐标变换使得它变为一个只包含平方项的简单形式。这在优化问题和概率论中非常重要。

## 4.4 小结

在本章中，我们深入探讨了特征值和特征向量的概念、求解方法和它们的性质，以及对角化的条件、过程和在变换中的应用。同时，还介绍了正定矩阵的判定方法以及二次型的简化过程。理解并掌握这些概念对于解决线性代数问题至关重要，也是深入学习更高级数学概念的基础。

在下一章中，我们将继续探索线性代数在各个实际问题中的应用，包括计算机科学、物理学、工程学以及经济学等领域的案例分析。

# 5. 线性代数在实际问题中的应用

线性代数作为数学的一个分支，在计算机科学、物理和工程学以及经济学等多个领域中都有着广泛的应用。它不仅为处理现实世界问题提供了强大的工具，而且还与最新技术的发展密切相关。本章节将探讨线性代数在这些领域的具体应用，并展示如何利用线性代数的概念解决实际问题。

## 5.1 线性代数在计算机科学中的应用

### 5.1.1 图论中的邻接矩阵与路径问题

在图论中，图是由顶点和连接顶点的边组成的抽象结构。在很多情况下，图中的顶点和边需要通过矩阵来表示。例如，邻接矩阵是一个非常重要的概念，用于表示图中各顶点之间的连接关系。对于无向图来说，邻接矩阵是对称的；而有向图的邻接矩阵则可能不对称。

import numpy as np

# 创建一个无向图的邻接矩阵示例
adjacency_matrix = np.array([
    [0, 1, 1, 0],
    [1, 0, 1, 0],
    [1, 1, 0, 1],
    [0, 0, 1, 0]
])

print("邻接矩阵:")
print(adjacency_matrix)

通过邻接矩阵，我们可以使用线性代数的方法解决各种路径问题，例如计算两点之间的最短路径、判断图的连通性等。最短路径问题可以通过矩阵运算来寻找解决方案，著名的Floyd-Warshall算法就是一个典型的例子。

### 5.1.2 机器学习中的矩阵运算与数据处理

机器学习依赖于大量的矩阵运算来实现其功能。从数据预处理、特征提取到模型训练，矩阵都是主要的数据结构。例如，使用矩阵的乘法可以实现线性变换，这在神经网络的权重更新以及主成分分析（PCA）中经常用到。

# 假设有一个数据矩阵X和一个权重矩阵W
X = np.array([[1, 2], [3, 4], [5, 6]])
W = np.array([[0.5, -0.2], [0.3, 0.8]])

# 应用权重矩阵变换数据
transformed_data = np.dot(X, W)
print("变换后的数据:")
print(transformed_data)

机器学习模型的训练过程中，矩阵运算加速了梯度下降等优化算法的执行。优化算法在每次迭代中，都需要对损失函数进行求导，并更新权重矩阵，这些都是通过矩阵运算实现的。

## 5.2 线性代数在物理和工程学中的应用

### 5.2.1 力学问题中的线性代数模型

在经典力学中，线性代数被用来描述物体的受力情况和运动状态。例如，在解决多质点系统的动力学问题时，质点的位置、速度和加速度等参数可以用向量表示，并通过矩阵运算来分析系统的动态行为。

# 假设有一个两质点系统，计算加速度矩阵
mass_matrix = np.array([[m1, 0], [0, m2]])  # 质量矩阵
force_matrix = np.array([[F1], [F2]])  # 力矩阵

# 根据牛顿第二定律，加速度矩阵等于力矩阵除以质量矩阵
acceleration_matrix = np.linalg.inv(mass_matrix).dot(force_matrix)
print("加速度矩阵:")
print(acceleration_matrix)

### 5.2.2 电路分析与矩阵方法

电路分析中，节点电压法和网孔电流法都依赖于线性代数方程。这些方程通常可以表示为矩阵形式，通过解线性方程组，可以计算出电路中各个节点的电压和各支路的电流。

# 设一个线性电路方程组为 Ax = b，其中A为系数矩阵，x为未知向量，b为常数向量
A = np.array([[R1 + R2, -R2], [-R2, R2 + R3]])
b = np.array([E, 0])  # 假设E为电源电压

# 通过线性代数方法求解线性方程组
solution = np.linalg.solve(A, b)
print("解得电流和电压:")
print(solution)

## 5.3 线性代数在经济学中的应用

### 5.3.1 投入产出分析与矩阵运算

在经济学中，线性代数被用于投入产出分析，其中列昂惕夫逆矩阵用于预测不同行业部门间的连锁效应。例如，增加某一部门的产出会如何影响其他部门的产出水平。

# 假设有一个投入产出矩阵A，和技术系数矩阵X
A = np.array([[0.1, 0.2], [0.3, 0.4]])
X = np.array([[100, 200], [300, 400]])

# 计算总产出Y，即Y = AX
total_output = np.dot(A, X)
print("总产出Y:")
print(total_output)

### 5.3.2 马尔可夫链与概率模型

马尔可夫链是一种特殊类型的随机过程，它描述了一系列事件中每个事件发生的概率仅依赖于前一个事件。在经济学中，马尔可夫链用于金融分析，比如预测股票价格的变动或信用评级的转换。

# 马尔可夫链转移矩阵P
P = np.array([[0.7, 0.2, 0.1], [0.3, 0.5, 0.2], [0, 0.4, 0.6]])

# 假设初始状态概率向量为 pi_0
pi_0 = np.array([0.5, 0.3, 0.2])

# 计算经过两步后的状态概率向量
pi_2 = np.dot(np.dot(pi_0, P), P)
print("经过两步后的状态概率向量:")
print(pi_2)

通过线性代数的概念和方法，我们可以将复杂的经济系统简化为数学模型，进一步分析和预测经济行为。线性代数不仅加深了我们对经济现象的理解，而且在决策制定中扮演了重要角色。