【Java Switch Case与函数式编程融合】：探索Lambda与Switch的完美结合

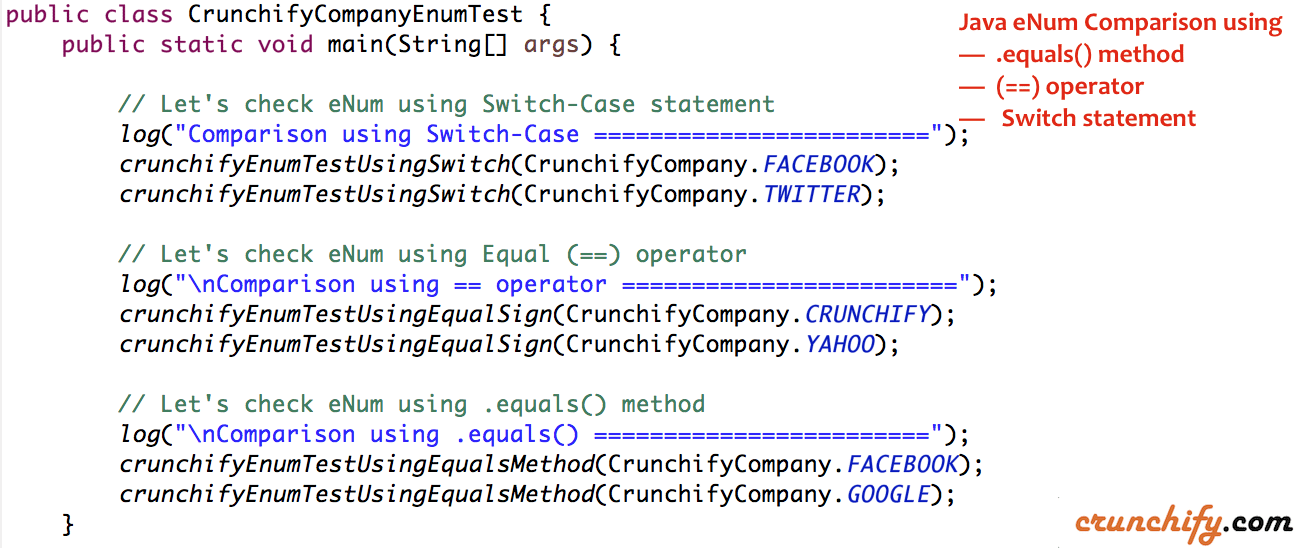
# 1. Java Switch Case的基础与历史回顾

## 1.1 Java Switch Case概述
Java中的Switch Case是一种多分支选择结构，允许基于不同的case标签执行相应的代码块。它在处理多条件判断时，相较于多个if-else语句来说，具有更高的可读性和执行效率。

## 1.2 Switch Case的历史演变
自Java 1.0起，Switch Case便被引入。随着时间的推移，它经历了多个版本的改进，例如在Java 12中引入的Switch表达式预览特性，这标志着Java对传统Switch的增强和现代化。

## 1.3 Switch Case在现代Java中的地位
尽管Lambda表达式的引入和函数式编程的流行可能已使Switch Case显得有些过时，但它们在处理固定数量的选项时仍保持了其独特价值。下一章，我们将探讨Lambda表达式的基础与演变，以及它们是如何影响Java编程范式。

# 2. 函数式编程的基本概念及在Java中的演变

函数式编程是一种编程范式，它的核心是使用函数作为一等公民，强调不变性和引用透明性。与命令式编程不同，函数式编程更关注的是计算的“做什么”，而不是“怎么做”。这种编程范式鼓励开发者通过组合纯函数来构建软件，避免共享状态、可变数据和副作用，从而使得程序更加简洁、易于理解且容易测试。

### 2.1 函数式编程基本概念

函数式编程起源于Lisp语言，其核心思想可以追溯到20世纪50年代，但是直到最近几十年才成为主流编程范式。函数式编程语言如Haskell、Erlang和Scala等都在推动这种范式的发展，而Java作为传统的面向对象编程语言，也逐渐向函数式编程靠拢。

#### 2.1.1 纯函数

在函数式编程中，纯函数是指对于相同的输入，总是返回相同的输出，且没有任何可观察的副作用的函数。纯函数的概念是函数式编程的基石，它使得函数可以被安全地重用和组合，同时简化了程序的推理和测试。

// 示例：Java中的纯函数
public int add(int a, int b) {
    return a + b;
}

上述`add`函数就是一个纯函数。它的输出仅依赖于输入参数，并且不会产生任何外部副作用。

#### 2.1.2 不可变性

不可变性是指数据一旦创建就不能被改变。在函数式编程中，不可变数据结构是常用的构建块。这有助于避免并发程序中出现的数据竞争和状态不一致问题。

// 示例：不可变数据结构的使用
final List<String> immutableList = List.of("apple", "banana", "cherry");

在Java中，`List.of`方法可以创建一个不可变的列表。一旦创建，就不能添加、删除或更改其元素。

#### 2.1.3 高阶函数

高阶函数是可以接受其他函数作为参数或返回一个函数作为结果的函数。它是函数式编程中实现抽象和模块化的重要工具。

// 示例：Java中的高阶函数
public static List<Integer> transform(List<Integer> list, Function<Integer, Integer> mapper) {
    List<Integer> result = new ArrayList<>();
    for (Integer item : list) {
        result.add(mapper.apply(item));
    }
    return result;
}

在上述代码中，`transform`函数是一个高阶函数，它接受一个`Function`类型的参数`mapper`，用于转换列表中的每个元素。

#### 2.1.4 延迟计算

延迟计算（Lazy Evaluation）是指表达式的计算直到需要其值时才进行。这种技术有助于提高程序的性能，尤其是在处理大量数据时。

// 示例：Java中的延迟计算
Stream<Integer> numbers = Stream.iterate(1, n -> n + 1)
                                .skip(1000)
                                .limit(10);
numbers.forEach(System.out::println);

在这个例子中，`iterate`方法创建了一个无限流，但是通过`skip`和`limit`方法，我们延迟了流的计算，只有当需要结果进行操作（如`forEach`）时，才会实际生成元素。

### 2.2 函数式编程在Java中的演变

Java是一种多范式编程语言，在其早期版本中主要强调面向对象编程。然而，从Java 8开始，Java引入了Lambda表达式和函数式接口，为函数式编程提供了支持。

#### 2.2.1 Lambda表达式的引入

Lambda表达式是一种简洁表示匿名函数的方式，它允许将函数作为参数传递，或者作为结果返回。Lambda表达式大大简化了Java中的事件处理和异步编程模式。

// 示例：Lambda表达式的基本使用
List<String> names = Arrays.asList("Alice", "Bob", "Charlie");
names.forEach(name -> System.out.println(name));

上述代码展示了如何使用Lambda表达式来遍历列表并打印每个元素。

#### 2.2.2 函数式接口

Java 8引入了函数式接口的概念，它是只有一个抽象方法的接口。这些接口通过`@FunctionalInterface`注解进行标记，使得Lambda表达式可以作为这些接口的实例。

// 示例：使用函数式接口
@FunctionalInterface
public interface Predicate<T> {
    boolean test(T t);
}

Predicate<String> predicate = s -> s.length() > 0;
boolean result = predicate.test("Hello, world!");

在这个例子中，`Predicate`是一个函数式接口，用于判断字符串是否非空。

#### 2.2.3 Stream API的集成

Java 8还引入了Stream API，它提供了一种高效且易于使用的处理集合数据的方式。Stream API支持函数式编程风格，并利用Lambda表达式进行操作。

// 示例：Stream API的使用
List<Integer> numbers = Arrays.asList(1, 2, 3, 4, 5);
int sum = numbers.stream()
                  .map(n -> n * n)
                  .reduce(0, Integer::sum);

在这个例子中，我们使用Stream API对数字列表进行处理，计算了它们平方的总和。

#### 2.2.4 方法引用

方法引用是一种使用Lambda表达式的简写方式，它允许直接引用现有的方法或构造函数。方法引用使得代码更加简洁和可读。

// 示例：方法引用的使用
List<String> names = Arrays.asList("Alice", "Bob", "Charlie");
names.forEach(System.out::println);

在这个例子中，我们使用了`System.out::println`方法引用代替了对应的Lambda表达式。

函数式编程为Java开发者带来了新的思维方式和工具，使得代码更加模块化、表达力更强，同时也提高了并发编程的安全性。随着Java社区对这种编程范式的不断探索和实践，函数式编程正在成为Java开发的一个重要组成部分。

# 3. Lambda表达式与Java函数式接口

## 3.1 Lambda表达式的原理和语法

### 3.1.1 Lambda表达式的基础

Lambda表达式是Java 8引入的一个核心特性，允许我们以一种简洁的方式表示匿名内部类。它本质上是一个可传递的代码块，可以在需要函数式接口实例的地方使用。Lambda表达式的基础格式如下：

参数 -> 表达式或语句块

其中，参数是指定的输入参数（可有可无），箭头（`->`）是Lambda操作符，表达式或语句块指Lambda的代码主体。

下面是一个简单的例子：

// 定义一个函数式接口
@FunctionalInterface
interface Sayable {
    void say(String message);
}

public class LambdaExample {
    public static void main(String[] args) {
        // 使用Lambda表达式调用say方法
        Sayable sayable = (message) -> System.out.println("Hello, " + message);
        sayable.say("Lambda Expressions!");
    }
}

在这个例子中，我们定义了一个函数式接口`Sayable`，并创建了一个Lambda表达式来实现`say`方法。这种方式大大简化了匿名类的复杂性，提高了代码的可读性。

### 3.1.2 Lambda与匿名类的区别

Lambda表达式与匿名类在概念上都用于创建函数式接口