Bzip2深度应用：Hadoop集群存储与I_O效率提升策略

# 1. Hadoop集群存储基础

在了解Hadoop集群存储基础之前，我们需要清楚Hadoop集群的核心功能是处理大数据。为了有效地存储和处理大量数据，Hadoop采用了分布式文件系统HDFS。本章节将对Hadoop集群存储的核心组件进行简单介绍，为后续深入探讨Bzip2压缩算法在Hadoop中的应用打下坚实的基础。

## 1.1 Hadoop集群存储组件

Hadoop集群存储主要包括以下几个关键组件：
- NameNode：负责管理文件系统的命名空间和客户端对文件的访问。
- DataNode：实际存储数据的地方，每个DataNode可能存储了文件系统中的一部分数据。
- Secondary NameNode：辅助NameNode，负责合并编辑日志和文件系统的元数据映像。

## 1.2 HDFS的工作原理

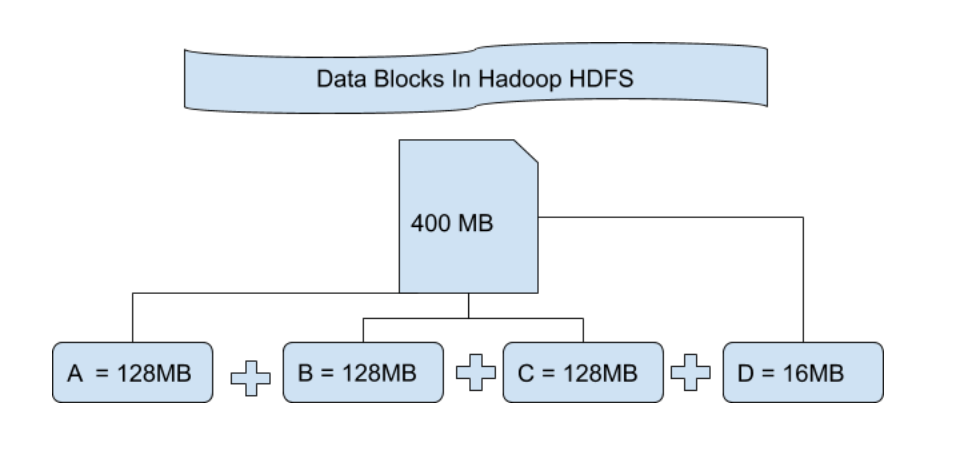
HDFS设计遵循“一次写入，多次读取”的原则，对于大规模数据集的存储十分高效。数据被分割成一系列的块（block），默认大小为128MB，这些块被分布式存储在多个DataNode上。在数据写入时，NameNode会指定DataNode来存储数据块，并且保持数据块的副本以提高数据的可靠性和容错性。

## 1.3 Hadoop集群存储的优势

Hadoop集群存储的主要优势在于其扩展性和容错性。由于HDFS的数据被分割成块，并且复制多份存储，即使部分节点发生故障，也不会影响整体数据的完整性和可访问性。此外，随着集群规模的扩大，其存储容量和处理能力可以线性增长，非常适合处理PB级别的数据。

通过初步了解Hadoop集群存储的基础知识，我们将继续深入探讨Bzip2压缩算法，以及其如何被集成进Hadoop集群，以及优化存储策略和提高I/O性能。

# 2. Bzip2压缩算法详解

## 2.1 Bzip2算法的工作原理

### 2.1.1 Bzip2的压缩流程

Bzip2 是一种基于 Burrows-Wheeler transform（BWT）、Move-to-Front（MTF）变换以及 Huffman 编码的压缩算法。BWT 是 Bzip2 算法的核心步骤，它将原始数据通过排列转换成更容易进行压缩处理的形式。MTF 变换进一步将 BWT 结果中的重复元素转换为更短的序列。最后，Huffman 编码为转换后的数据生成压缩的位流。

以下是 Bzip2 压缩流程的概述：

1. **输入数据缓冲**：输入数据首先被缓存到一个足够大的缓冲区中，以便 BWT 可以在没有数据丢失的情况下进行。
2. **BWT 变换**：将缓冲区的数据进行 BWT，生成一个排列矩阵。BWT 不是一个可逆过程，但通过后续的步骤可以恢复原始数据。
3. **MTF 变换**：将 BWT 的结果作为输入，通过 MTF 变换，把出现频率较高的字符放到列表的前面。
4. **游程编码（Run-Length Encoding, RLE）**：对于 MTF 结果中连续出现的重复字符进行游程编码，以减少数据量。
5. **Huffman 编码**：对经过游程编码的数据进行 Huffman 编码，生成最终的压缩数据。Huffman 编码是一种无损压缩方法，通过为常见的数据模式分配较短的编码，而较少出现的模式分配较长的编码。

### 2.1.2 Bzip2与其他压缩算法的比较

Bzip2 在数据压缩率和速度方面与其他算法（如 gzip 和 LZMA）相比有其独特的优势和局限性。下表列出了一些常见的压缩算法及其特点，以便进行比较：

| 算法 | 压缩率 | 压缩速度 | 解压速度 | 复杂度 | 备注 |
|------|-------|---------|---------|-------|-----|
| Bzip2 | 较高 | 较慢 | 较快 | 中等 | 适合文本文件 |
| gzip | 中等 | 较快 | 非常快 | 低 | 广泛使用，适用于多种数据类型 |
| LZMA | 很高 | 很慢 | 较慢 | 高 | 高压缩率但速度较慢 |

从上表可以看出，Bzip2 在压缩率上通常优于 gzip，但压缩速度更慢，解压速度相对较快。对于需要高压缩率但解压速度要求不是最高的场合，Bzip2 是一个很好的选择。然而，对于速度要求极高的场景，gzip 或其他压缩算法可能更合适。

## 2.2 Bzip2在Hadoop中的集成

### 2.2.1 Hadoop对Bzip2的支持

Hadoop 作为一个大数据处理框架，提供了对多种压缩格式的支持，包括 Bzip2。从 Hadoop 0.20 版本开始，Bzip2 已被官方支持。在 Hadoop 中使用 Bzip2 压缩数据可以有效地减少存储空间的需求，虽然以牺牲一些 CPU 资源和时间来实现压缩和解压。

### 2.2.2 配置Bzip2压缩的Hadoop环境

要配置 Hadoop 以使用 Bzip2 压缩，需要对 `core-site.xml` 文件进行相应的设置。以下是配置 Bzip2 的关键步骤：

1. **添加 Hadoop 库路径**：首先，确保 `hadoop-common-x.y.z.jar` 包含 Bzip2 的支持。通常，Bzip2 支持是 Hadoop 核心库的一部分，无需额外添加。

2. **配置 Hadoop 配置文件**：编辑 `core-site.xml` 文件，添加如下配置以启用 Bzip2 压缩：

<configuration>
    <property>
        <name>***pression.codecs</name>
        <value>
            ***press.DefaultCodec,
            ***press.GzipCodec,
            ***press.BZip2Codec,
            ***press.DeflateCodec,
            ***press.SnappyCodec
        </value>
    </property>
</configuration>

通过以上步骤，Hadoop 环境已经配置完毕，可以支持 Bzip2 压缩了。接下来，可以设置 MapReduce 作业或 HDFS 文件系统在创建文件时使用 Bzip2 压缩。

hadoop fs -put -compress bzip2 input.txt output.txt.bz2

这个命令会将 `input.txt` 文件使用 Bzip2 压缩后存储为 `output.txt.bz2`。

请注意，配置 Hadoop 环境来支持 Bzip2 可能需要重启集群，以确保所有配置更改生效。

# 3. Bzip2在Hadoop集群中的应用实践

Hadoop作为一个强大的分布式存