线性相位滤波器在图像处理中的应用：探索其优势和局限

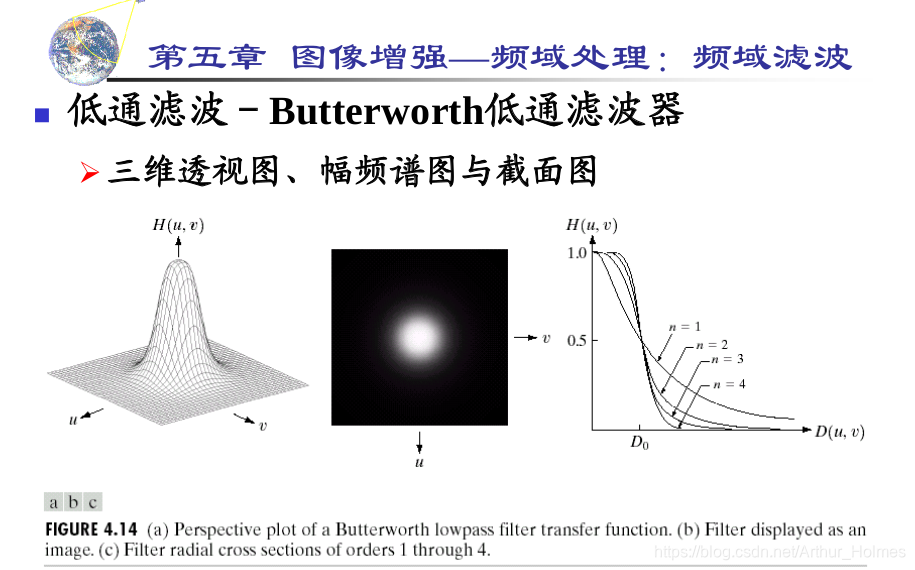
# 1. 线性相位滤波器的理论基础

线性相位滤波器是一种数字图像处理技术，其核心思想是通过改变图像的相位信息来实现图像增强和复原。与传统滤波器不同，线性相位滤波器在处理图像时保持图像的边缘清晰度，避免了图像失真。

线性相位滤波器的理论基础建立在傅里叶变换的基础上。傅里叶变换将图像从空间域转换为频域，其中图像的相位信息与图像的边缘和纹理特征相关。通过对频域图像进行线性相位操作，可以实现图像的增强和复原。

# 2. 线性相位滤波器的设计与实现

### 2.1 线性相位滤波器的设计方法

#### 2.1.1 窗函数法

**原理：**

窗函数法是一种通过乘以窗函数来设计线性相位滤波器的方法。窗函数是一种在频域具有特定形状的函数，它可以用来抑制滤波器响应中的不必要频率分量。

**步骤：**

1. 选择一个理想的频率响应。
2. 设计一个窗函数，其频谱与理想响应的形状相匹配。
3. 将理想响应与窗函数相乘，得到线性相位滤波器的频率响应。

**优势：**

* 设计简单，易于实现。
* 可以设计出各种形状的滤波器。

**局限：**

* 窗函数会引入一些失真。
* 对于高阶滤波器，窗函数的长度会很长。

#### 2.1.2 反投影法

**原理：**

反投影法是一种通过反投影操作来设计线性相位滤波器的方法。反投影操作是指将滤波器的频率响应投影到时域，然后将其反投影回频域。

**步骤：**

1. 选择一个理想的时域响应。
2. 将理想响应反投影到频域，得到滤波器的频率响应。
3. 将频率响应反投影回时域，得到线性相位滤波器的时域响应。

**优势：**

* 可以设计出具有任意相位响应的滤波器。
* 对于高阶滤波器，反投影法的计算量较小。

**局限：**

* 设计过程复杂，需要使用数值方法。
* 对于某些滤波器，反投影法可能会产生不稳定的结果。

### 2.2 线性相位滤波器的实现技术

#### 2.2.1 时域实现

**原理：**

时域实现是指直接在时域中实现线性相位滤波器。这种方法需要使用卷积操作，将滤波器核与输入信号进行卷积。

**代码示例：**

import numpy as np

def linear_phase_filter_time_domain(signal, filter_kernel):
    """
    时域实现线性相位滤波器。

    参数：
        signal: 输入信号。
        filter_kernel: 滤波器核。

    返回：
        滤波后的信号。
    """

    # 计算卷积
    filtered_signal = np.convolve(signal, filter_kernel, mode='same')

    return filtered_signal

**逻辑分析：**

* `np.convolve()` 函数执行卷积操作，将 `filter_kernel` 与 `signal` 进行卷积。
* `mode='same'` 参数指定使用相同填充，这意味着滤波后的信号长度与输入信号长度相同。

#### 2.2.2 频域实现

**原理：**

频域实现是指将线性相位滤波器转换为频域，然后使用快速傅里叶变换 (FFT) 进行滤波。这种方法可以避免卷积操作，从而提高计算效率。

**代码示例：**

import numpy as np
from scipy.fftpack import fft, ifft

def linear_phase_filter_frequency_domain(signal, filter_kernel):
    """
    频域实现线性相位滤波器。

    参数：
        signal: 输入信号。
        filter_kernel: 滤波器核。

    返回：
        滤波后的信号。
    """

    # 将信号和滤波器核转换为频域
    signal_fft = fft(signal)
    filter_kernel_fft = fft(filter_kernel)

    # 乘以滤波器响应
    filtered_signal_fft = signal_fft * filter_kernel_fft

    # 将滤波后的信号转换回时域
    filtered_signal = ifft(filtered_signal_fft)

    return filtered_signal

**逻辑分析：**

* `fft()` 函数将 `signal` 和 `filter_kernel` 转换为频域。
* `filtered_signal_fft` 是 `signal_fft` 与 `filter_kernel_fft` 的乘积，表示滤波后的信号在频域中的响应。
* `ifft()` 函数将 `filtered_signal_fft` 转换回时域，得到滤波后的信号。

# 3. 线性相位滤波器在图像处理中的应用

线性相位滤波器在图像处理领域有着广泛的应用，主要体现在图像增强和图像复原两个方面。

### 3.1 图像增强

图像增强旨在改善图像的视觉效果，使其更易于理解和分析。线性相位滤波器可以用于图像锐化和去噪。

#### 3.1.1 图像锐化

图像锐化是指增强图像中边缘和细节的清晰度。线性相位滤波器通过去除图像中的低频分量来实现锐化。常用的线性相位锐化滤波器包括拉普拉斯算子、Sobel算子和Prewitt算子。

**代码块：**

import cv2
import numpy as np

# 图像锐化
def sharpen(image):
    # 拉普拉斯算子
    kernel = np.array([[0, -1, 0],
                       [-1, 5, -1],
                       [0, -1, 0]])
    # 频域实现
    dft = cv2.dft(np.float32(image), flags=cv2.DFT_COMPLEX_OUTPUT)
    dft_shift = np.fft.fftshift(dft)
    magnitude_spectrum = 20 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))
    # 锐化滤波
    dft_shift[:, :, 0] = dft_shift[:, :, 0] * kernel
    dft_shift[:, :, 1] = dft_shift[:, :, 1] * kernel
    # 逆变换
    inverse_dft = np.fft.ifftshift(dft_shift)
    result = cv2.idft(inverse_dft, flags=cv2.DFT_SCALE | cv2.DFT_REAL_OUTPUT)
    return result.astype(np.uint8)

**逻辑分析：**

* 拉普拉斯算子是一个 3x3 的线性相位滤波器，它通过增强图像中的高频分量来实现锐化。
* 频域实现通过将图像转换为频域，对频谱进行滤波，然后逆变换回时域来实现锐化。
* `magnitude_spectrum` 用于可视化频谱的变化。

#### 3.1.2 图像去噪

图像去噪是指从图像中去除噪声，以提高图像的质量。线性相位滤波器可以通过滤除图像中的高频分量来实现去噪。常用的线性相位去噪滤波器包括均值滤波器、中值滤波器和维纳滤波器。

**代码块：**

import cv2
import numpy as np

# 图像去噪
def denoise(image):
    # 均值滤波器
    kernel = np.ones((3, 3), np.float32) / 9
    # 时域实现
    result = cv2.filter2D(image, -1, kernel)
    return result.astype(np.uint8)

**逻辑分析：**

* 均值滤波器是一个 3x3 的线性相位滤波器，它通过计算邻域像素的平均值来平滑图像。
* 时域实现直接在图像上进行滤波，计算效率高。

### 3.2 图像复原

图像复原旨在恢复图像中丢失或损坏的信息。线性相位滤波器可以用于图像去模糊和超分辨。

#### 3.2.1 图像去模糊

图像去模糊是指去除图像中的模糊，以恢复清晰的图像。线性相位滤波器可以通过逆滤波或维纳滤波来实现去模糊。

**代码块：**

import cv2
import numpy as np

# 图像去模糊
def deblur(image, kernel):
    # 逆滤波
    dft = cv2.dft(np.float32(image), flags=cv2.DFT_COMPLEX_OUTPUT)
    dft_shift = np.fft.fftshift(dft)
    # 逆滤波器
    H = np.conj(kernel) / (np.abs(kernel) ** 2 + 0.0001)
    # 滤波
    dft_shift[:, :, 0] = dft_shift[:, :, 0] * H
    dft_shift[:, :, 1] = dft_shift[:, :, 1] * H
    # 逆变换
    inverse_dft = np.fft.ifftshift(dft_shift)
    result = cv2.idft(inverse_dft, flags=cv2.DFT_SCALE | cv2.DFT_REAL_OUTPUT)
    return result.astype(np.uint8)

**逻辑分析：**

* 逆滤波通过将模糊核的共轭除以其幅度平方来构造逆滤波器。
* 滤波在频域中进行，可以有效去除模糊。

#### 3.2.2 图像超分辨

图像超分辨是指从低分辨率图像中恢复高分辨率图像。线性相位滤波器可以通过插值或反投影法来实现超分辨。

**代码块：**

import cv2
import numpy as np

# 图像超分辨
def super_resolution(image, scale):
    # 反投影法
    # 创建高分辨率图像
    hr_image = np.zeros((image.shape[0] * scale, image.shape[1] * scale), np.uint8)
    # 反投影
    for i in range(image.shape[0]):
        for j in range(image.shape[1]):
            hr_image[i*scale:(i+1)*scale, j*scale:(j+1)*scale] = image[i, j]
    # 插值
    hr_image = cv2.resize(hr_image, (image.shape[1] * scale, image.shape[0] * scale), interpolation=cv2.INTER_CUBIC)
    return hr_image

**逻辑分析：**

* 反投影法通过将低分辨率图像中的像素复制到高分辨率图像中来实现超分辨。
* 插值用于平滑高分辨率图像中的像素。

# 4.1 线性相位滤波器的优势

线性相位滤波器在图像处理中具有以下优势：

### 4.1.1 保持图像的边缘清晰度

线性相位滤波器在滤波过程中不会改变图像的相位，因此可以有效地保持图像的边缘清晰度。这是因为相位信息与图像的边缘特征密切相关。当相位发生变化时，图像的边缘就会变得模糊。

### 4.1.2 避免图像失真

线性相位滤波器不会引入相位失真，因此可以避免图像出现失真现象。相位失真会导致图像出现条纹、波纹等伪影，影响图像的视觉质量。

### 4.1.3 适用于高频信号处理

线性相位滤波器特别适用于高频信号的处理。在高频信号中，相位信息非常重要，因此线性相位滤波器可以有效地保留这些信息，避免失真。

### 4.1.4 容易实现

线性相位滤波器相对容易实现，可以使用时域或频域的方法。时域实现直接在图像像素上进行操作，而频域实现则将图像转换为频域，再进行滤波操作。

## 4.2 线性相位滤波器的局限

尽管线性相位滤波器具有许多优势，但它也存在一些局限：

### 4.2.1 计算量大

线性相位滤波器通常需要进行大量的计算，特别是对于大尺寸图像。这是因为线性相位滤波器需要对图像中的每个像素进行操作，并且需要迭代多次才能达到理想的滤波效果。

### 4.2.2 对于某些图像噪声效果不佳

线性相位滤波器对于某些类型的图像噪声效果不佳，例如椒盐噪声和高斯噪声。这是因为线性相位滤波器主要针对相位失真进行滤波，而对于其他类型的噪声则效果有限。

### 4.2.3 滤波效果受限

线性相位滤波器只能对图像进行线性滤波，对于非线性滤波需求，线性相位滤波器无法满足。

# 5. 线性相位滤波器的优化与改进

线性相位滤波器虽然具有良好的性能，但仍存在一些局限性，如计算量大、对于某些图像噪声效果不佳等。为了克服这些局限性，研究人员提出了各种优化算法和滤波器改进方法。

### 5.1 优化算法

优化算法旨在通过调整滤波器参数，提高滤波器的性能。常用的优化算法包括：

#### 5.1.1 梯度下降法

梯度下降法是一种迭代算法，通过计算滤波器参数的梯度，并沿着梯度负方向更新参数，从而使目标函数最小化。目标函数可以是滤波器输出图像的均方误差、峰值信噪比等。

import numpy as np

def gradient_descent(filter, image, target, learning_rate):
    """
    梯度下降法优化线性相位滤波器

    参数：
        filter: 线性相位滤波器
        image: 输入图像
        target: 目标图像
        learning_rate: 学习率

    返回：
        优化后的线性相位滤波器
    """

    # 计算滤波器参数的梯度
    gradient = np.gradient(filter)

    # 更新滤波器参数
    filter -= learning_rate * gradient

    return filter

#### 5.1.2 共轭梯度法

共轭梯度法是一种改进的梯度下降法，它利用共轭方向来加快收敛速度。共轭方向是一组正交向量，可以使优化过程沿最陡下降的方向进行。

import numpy as np

def conjugate_gradient(filter, image, target, learning_rate):
    """
    共轭梯度法优化线性相位滤波器

    参数：
        filter: 线性相位滤波器
        image: 输入图像
        target: 目标图像
        learning_rate: 学习率

    返回：
        优化后的线性相位滤波器
    """

    # 计算滤波器参数的梯度
    gradient = np.gradient(filter)

    # 初始化共轭方向
    conjugate_direction = -gradient

    # 迭代优化
    while True:
        # 计算共轭方向的梯度
        conjugate_gradient = np.gradient(conjugate_direction)

        # 计算步长
        step_size = np.dot(gradient, conjugate_direction) / np.dot(conjugate_gradient, conjugate_gradient)

        # 更新滤波器参数
        filter -= step_size * conjugate_direction

        # 更新梯度和共轭方向
        gradient = np.gradient(filter)
        conjugate_direction = -gradient + step_size * conjugate_gradient

        # 判断是否收敛
        if np.linalg.norm(gradient) < 1e-6:
            break

    return filter

### 5.2 滤波器改进

除了优化算法外，还可以通过改进滤波器结构来提高其性能。常见的滤波器改进方法包括：

#### 5.2.1 分段线性相位滤波器

分段线性相位滤波器将滤波器频域响应的相位曲线划分为多个线性段，从而降低计算量。

import numpy as np

def segmented_linear_phase_filter(filter_size, num_segments):
    """
    生成分段线性相位滤波器

    参数：
        filter_size: 滤波器尺寸
        num_segments: 线性段数量

    返回：
        分段线性相位滤波器
    """

    # 初始化滤波器
    filter = np.zeros((filter_size, filter_size))

    # 计算每个线性段的相位增量
    phase_increment = np.pi / num_segments

    # 遍历每个线性段
    for i in range(num_segments):
        # 计算线性段的起始和结束频率
        start_freq = i * phase_increment
        end_freq = (i + 1) * phase_increment

        # 计算线性段的相位函数
        phase = np.linspace(start_freq, end_freq, filter_size)

        # 将相位函数应用到滤波器
        filter += np.exp(-1j * phase)

    return filter

#### 5.2.2 非线性相位滤波器

非线性相位滤波器使用非线性函数来设计滤波器相位响应，从而提高滤波器的鲁棒性和噪声抑制能力。

import numpy as np

def nonlinear_phase_filter(filter_size, nonlinearity):
    """
    生成非线性相位滤波器

    参数：
        filter_size: 滤波器尺寸
        nonlinearity: 非线性函数

    返回：
        非线性相位滤波器
    """

    # 初始化滤波器
    filter = np.zeros((filter_size, filter_size))

    # 计算滤波器频域响应的幅度
    amplitude = np.ones((filter_size, filter_size))

    # 计算滤波器频域响应的相位
    phase = nonlinearity(np.linspace(-np.pi, np.pi, filter_size))

    # 将幅度和相位应用到滤波器
    filter = amplitude * np.exp(-1j * phase)

    return filter

# 6. 线性相位滤波器的应用前景与展望

### 6.1 未来发展趋势

#### 6.1.1 深度学习与线性相位滤波器的结合

深度学习在图像处理领域取得了显著的成就，其强大的特征提取和非线性映射能力为线性相位滤波器的优化和改进提供了新的思路。通过将深度学习技术与线性相位滤波器相结合，可以实现更精细的图像处理效果。

#### 6.1.2 可重构线性相位滤波器

可重构线性相位滤波器是指能够根据不同的图像内容和处理需求动态调整其相位响应的滤波器。通过采用可重构技术，线性相位滤波器可以实现更灵活、更适应性的图像处理。

### 6.2 应用领域拓展

#### 6.2.1 医学图像处理

线性相位滤波器在医学图像处理中具有广阔的应用前景。例如，在医学影像的增强、去噪和复原方面，线性相位滤波器可以有效地提高图像质量，辅助医生进行疾病诊断。

#### 6.2.2 工业图像处理

在工业图像处理中，线性相位滤波器可以用于缺陷检测、质量控制和自动化生产。通过对工业图像进行锐化、去噪和复原处理，可以提高缺陷识别的准确性和效率。