HEC-HMS交叉验证：如何评估模型的预测能力


参考资源链接：[HEC-HMS洪水模拟操作指南：从流域处理到参数调整](https://wenku.csdn.net/doc/bg1kwrp8qz?spm=1055.2635.3001.10343)
# 1. HEC-HMS模型概述

## 简介
HEC-HMS（Hydrologic Modeling System）是由美国陆军工程兵团水文工程中心开发的一款水文模拟软件。其主要目标是提供一个集成化、用户友好的界面，用于模拟水文过程，帮助水文学家、工程师和规划师在不同尺度上进行水文分析和设计。

## 功能与应用
HEC-HMS能够模拟各种水文过程，包括流域汇流、基流、水库操作、地下水补给和损失。它适用于多种应用，如洪水预报、水资源规划、环境影响评估和洪水风险管理等。

## 模型结构
模型核心由几个关键组件构成：流域描述器、损失方法、转化方法、汇流方法以及控制模块。流域描述器定义了水文单元和它们的相互关系；损失方法和转化方法处理降雨输入和地表径流的产生；汇流方法模拟流量的沿程变化；控制模块则用于设置模拟的运行时间、数据输入输出等。

HEC-HMS模型因其灵活性和模块化设计，在国内外被广泛应用。下一章我们将深入探讨HEC-HMS模型的预测能力的理论基础，以及其核心工作原理。

# 2. HEC-HMS模型预测能力的理论基础

## 2.1 水文模型理论
### 2.1.1 水文循环与水文过程
水文循环是自然界的水不断循环的动态过程，包括蒸发、凝结、降水、径流和渗透等环节。水文模型是对这一过程的数学表达，目的是模拟自然界中水分的运动和转化。

水文过程是水文循环的具体表现形式，它涵盖了从降水到地表径流、地下水流以及流域出流的全过程。HEC-HMS模型通过数学方程和物理参数来模拟这些过程，能够帮助我们理解和预测流域的水文响应。

### 2.1.2 水文模拟的数学基础
水文模拟的数学基础主要包括微分方程、概率论和统计学。微分方程用于描述水文过程中的连续变化，概率论用于处理水文事件的随机性和不确定性，统计学则提供了数据分析和模型校正的方法。

微分方程组如连续方程和动量方程是描述水体运动的基本工具，它们通过空间和时间的积分形式连接了水文变量。这些方程可以是线性或非线性的，取决于所研究的水文过程的复杂性。

## 2.2 HEC-HMS模型的工作原理
### 2.2.1 模型的组成和结构
HEC-HMS模型主要由几个关键模块组成，包括流域描述、降雨-径流模型、水文响应单元（HRUs）、损失模型、转化模型和流量叠加等。这些模块共同构成了模型的结构框架。

流域描述模块提供了流域的地形、土壤类型、植被覆盖等基础信息。降雨-径流模型根据降水数据和流域特征生成径流数据。损失模型计算了降雨中无法形成径流的部分。转化模型将径流从流域特定位置转移到流域出口。最终，流量叠加模块汇总所有径流，得到流域出口的总流量。

### 2.2.2 模型参数的设置和校正
模型参数设置是建立HEC-HMS模型的关键步骤，需要根据实际流域的物理特性进行。参数的校正是通过比较模型输出与实际观测数据，对模型进行调整，以提高模拟的准确性。

参数校正通常使用自动校准工具，如HEC-HMS的优化工具包，它采用遗传算法、模拟退火等优化方法寻找最优参数集。这一过程包括确定目标函数、选择合适的数据集、运行模型和评估模型输出等步骤。

## 2.3 交叉验证的概念和重要性
### 2.3.1 统计学中的交叉验证方法
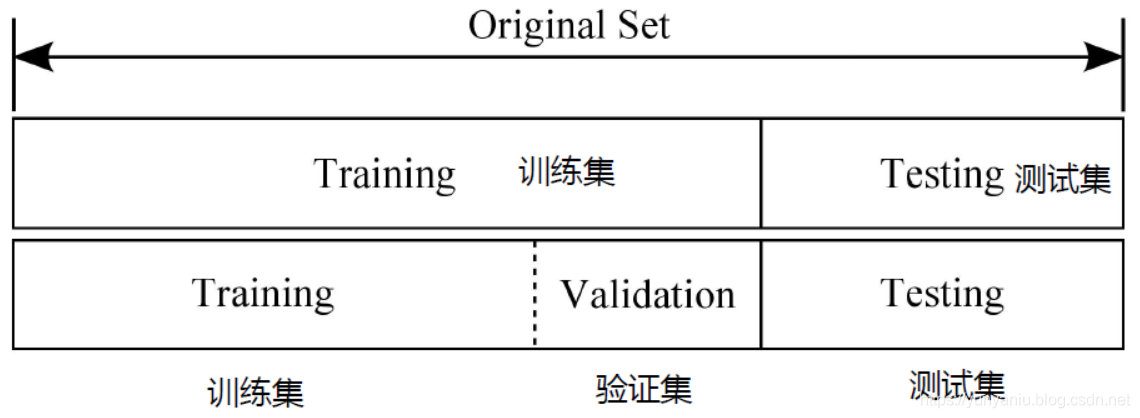
交叉验证是一种统计学方法，用于评估模型的泛化能力，即将数据分成多个部分，轮流使用其中一部分作为验证集，其余作为训练集，从而验证模型在未知数据上的表现。

这种方法特别适用于小数据集的建模场景，能够有效地评估模型的稳定性和准确性。在HEC-HMS模型中，交叉验证帮助我们了解模型对于不同降雨事件的响应情况。

### 2.3.2 在HEC-HMS模型中的应用
在HEC-HMS模型中，交叉验证通常用于评估降雨-径流模型的预测能力。通过分析模型在不同子集数据上的预测结果，可以识别模型的不足之处并进行优化。

交叉验证的实施也促进了模型参数的校正，提供了多个独立评估的机会，使得模型的参数设置更加精确和可靠。

> 注意：在实际操作中，HEC-HMS模型的交叉验证需要考虑多种因素，如流域特性、模型结构、输入数据的质量等。

# 3. HEC-HMS模型预测能力的评估方法

## 3.1 评估指标的选择

水文模型的预测能力评估是确保模型可靠性与有效性的核心环节。选择恰当的评估指标对于理解模型性能至关重要，它能够为模型的调整和应用提供科学依据。

### 3.1.1 常用的性能评估指标

在水文预测领域，常用的性能评估指标包括确定性系数（如 Nash-Sutcliffe Efficiency, NSE），偏差度量（如 Percent Bias, PBIAS），以及根均方误差（Root Mean Square Error, RMSE）等。

#### 确定性系数 NSE

NSE是衡量模型预测与实际观测拟合程度的重要指标，其值范围在负无穷到1之间，值越接近1表示模型预测越准确。

公式表示为：
\[ NSE = 1 - \frac{\sum_{i=1}^{n}(Q_{obs,i} - Q_{sim,i})^2}{\sum_{i=1}^{n}(Q_{obs,i} - \overline{Q_{obs}})^2} \]

其中，\(Q_{obs,i}\) 为实际观测值，\(Q_{sim,i}\) 为模型模拟值，\(\overline{Q_{obs}}\) 为观测值的平均值。

#### 偏差度量 PBIAS

PBIAS用于评估模型预测的平均偏差程度，可以是正数或负数，其理想值接近0。

公式表示为：
\[ PBIAS = \left( \frac{\sum_{i=1}^{n}(Q_{obs,i} - Q_{sim,i})}{\sum_{i=1}^{n}Q_{obs,i}} \right) \times 100 \]

#### 根均方误差 RMSE

RMSE用于衡量预测值与实际观测值之间差异的大小，其值越小表示模型预测误差越小。

公式表示为：
\[ RMSE = \sqrt{\frac{\sum_{i=1}^{n}(Q_{obs,i} - Q_{sim,i})^2}{n}} \]

其中，\(n\) 为观测值的数量。

### 3.1.2 指标的解释和应用场景

确定性系数（NSE）特别适用于评估模型在解