C++位运算技巧：位运算解决数学问题，效率倍增

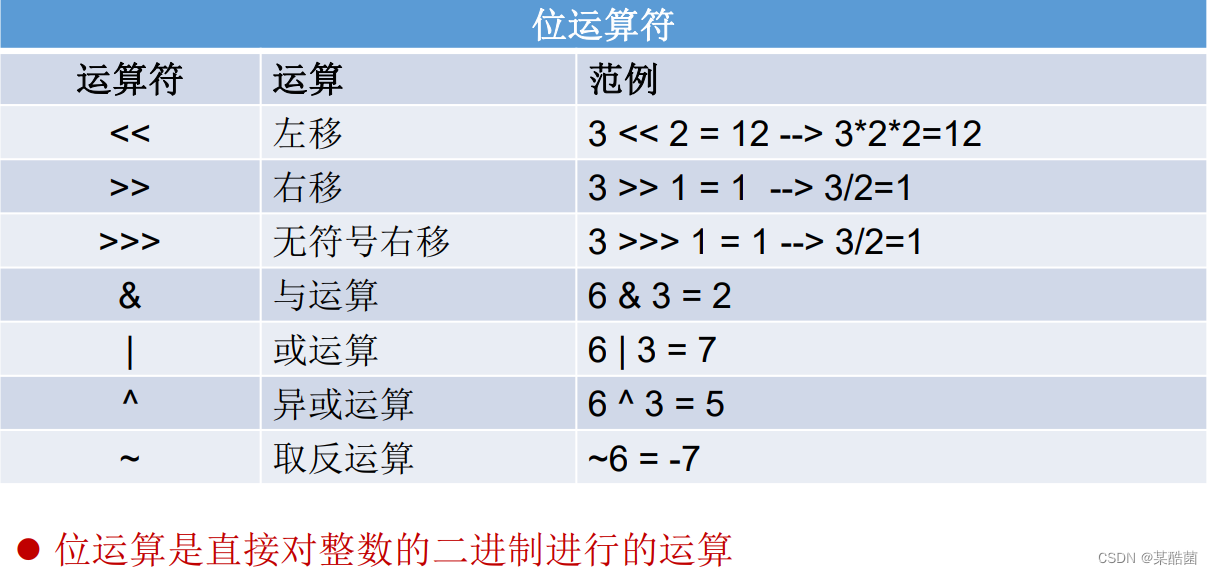
# 1. C++位运算基础与原理

在计算机科学中，位运算是一种低级的运算方式，直接对内存中的二进制位进行操作。在C++编程语言中，位运算符允许程序员执行一系列位级操作，包括位与(&)、位或(|)、位异或(^)、位非(~)、左移(<<)和右移(>>)。理解这些基本操作是掌握位运算原理的第一步。

## 2.1 位运算的基本概念

### 2.1.1 位运算符的种类和作用
- 位与(&)：将两个数的每一位进行逻辑与操作，只有两个数在同一位置的位都是1时结果位才是1。
- 位或(|)：将两个数的每一位进行逻辑或操作，只要两个数在同一位置的位有一个是1时结果位就是1。
- 位异或(^)：将两个数的每一位进行逻辑异或操作，当两个数在同一位置的位不相同时结果位为1，相同时为0。
- 位非(~)：将一个数的每一位取反，即0变为1，1变为0。
- 左移(<<)：将数字的二进制位向左移动指定位数，右边空出的位用0填充。
- 右移(>>)：将数字的二进制位向右移动指定位数，左边空出的位用原最高位的值填充（算术右移），或用0填充（逻辑右移）。

### 2.1.2 位运算的二进制表示法
位运算是在二进制层面上进行的，因此理解二进制表示法对于掌握位运算至关重要。每个二进制位代表一个2的幂次方值，从右到左分别是2^0, 2^1, 2^2, ...等等。

通过熟练掌握这些基本的位运算符和二进制表示法，程序员能够更加高效地处理数据，并解决各种低级计算问题。在接下来的章节中，我们将进一步探索位运算在数学问题中的应用，以及如何使用位运算来提高算法效率和解决实际问题。

# 2. 位运算在数学问题中的应用

### 2.1 位运算的基本概念

#### 2.1.1 位运算符的种类和作用

位运算符是直接对数据的二进制位进行操作的运算符，包括按位与（&）、按位或（|）、按位异或（^）、按位取反（~）、左移（<<）和右移（>>）。这些运算符在处理数字的内部表示时非常有效率。

例如，按位与（&）运算符，对两个数的每一位进行与操作，只有两个数在该位都为1时，结果位才为1。对于数据的某些特定部分进行掩码操作时十分有用。假设我们要清除一个整数的最后四位，可以使用如下的表达式：

int mask = 0xF0; // *** in binary
int value = 0xABCD; // *** in binary
int result = value & mask; // *** in binary

在这个例子中，我们创建了一个掩码 `mask` 来保留高四位，而将低四位与0进行与操作，从而将其置为0。

#### 2.1.2 位运算的二进制表示法

了解位运算符的二进制表示法对深入理解位运算至关重要。每一位都是一个二进制数字（0 或 1），而一个字节则由8位组成。当我们使用位运算符时，实际上是直接在这些二进制位上执行逻辑运算。

下面是一个按位或（|）运算符的二进制运算示例：

int num1 = 0b101010; // 42 in decimal
int num2 = 0b110000; // 48 in decimal
int result = num1 | num2; // 0b111010 in binary (58 in decimal)

在这个例子中，`num1` 和 `num2` 的二进制形式分别是 `101010` 和 `110000`。使用按位或运算后，我们得到 `111010`，即十进制数58。

### 2.2 位运算的数学性质

#### 2.2.1 位运算与算术运算的关系

位运算是构建算术运算的基础。例如，加法可以用左移和按位或运算来模拟：

unsigned int add(unsigned int x, unsigned int y) {
    while (y != 0) {
        // carry now contains common set bits of x and y
        unsigned int carry = x & y;

        // Sum of bits of x and y where at least one of the bits is not set
        x = x ^ y;

        // Carry is shifted by one so that adding it to x gives the required sum
        y = carry << 1;
    }
    return x;
}

此函数模拟了加法的逐位求和过程，通过迭代处理进位情况。

#### 2.2.2 利用位运算实现快速乘除法

位运算可以用来实现比传统算术运算更快的乘除法操作。例如，乘以2的幂可以通过左移操作简单实现。

int multiplyByTwo(int n) {
    return n << 1; // equivalent to n * 2
}

通过右移操作可以实现除以2的幂的操作。

### 2.3 位运算解题技巧

#### 2.3.1 位运算解决问题的思路

位运算提供了一种高效的方法来解决特定类型的问题。在处理整数集合和优化状态存储方面尤为有用。

例如，利用位掩码来标记和检查一组元素是否被选中。每个比特位代表一个元素是否被选中，通过位运算可以快速更新和查询状态。

#### 2.3.2 典型问题的位运算解法分析

位运算解题的一个典型应用是快速幂运算。快速幂可以使用位运算来将幂的指数转换为二进制形式，并且只对指数中为1的位进行乘法操作。

int fastPower(int base, int exp) {
    int result = 1;
    while (exp > 0) {
        if (exp & 1) {
            result *= base;
        }
        base *= base;
        exp >>= 1;
    }
    return result;
}

在这个算法中，我们检查指数的每一位，如果为1，则将基数乘以当前的结果。同时，基数自身进行平方操作，而指数每次右移一位，相当于除以2。

这个方法相比朴素的幂计算方法大大降低了运算次数，提高了效率。

以上章节展示了位运算在数学问题中的基础应用，从基本概念到具体技巧，通过逐步深入的解析，我们可以看到位运算在解决数学问题时的多样性和效率。在后续的章节中，我们将探讨位运算在算法效率优化、数据结构、编码技巧以及复杂问题中的深入应用。

# 3. 位运算优化算法效率

## 3.1 位运算与算法性能
在计算领域，算法的效率是衡量程序优劣的关键指标之一。位运算，作为计算机科学中的基本操作，对于提升算法性能有着不可忽视的作用。

### 3.1.1 时间复杂度与空间复杂度的优化
时间复杂度与空间复杂度是评估算法性能的两个重要参数。通过使用位运算，我们可以在某些情况下减少运算的步骤，降低时间复杂度，同时位运算还可以减少内存的使用，优化空间复杂度。

- **时间复杂度优化**：位运算通常具有较低的时间复杂度。例如，在处理集合操作时，使用位运算可以快速进行并集、交集、差集等操作。特别是对于大规模数据处理时，位运算比传统循环方法要快得多。
- **空间复杂度优化**：位运算使用位级操作，相比使用整型、浮点型等数据类型可以显著减少内存占用。例如，在实现一些状态存储时，可以使用单个字节的位来代表八个状态，而不是使用一个单独的变量。

下面是一个时间复杂度优化的示例代码：

// 使用位运算计算二进制中1的个数，时间复杂度为O(log n)
int countSetBits(int n) {
    int count = 0;
    while (n) {
        count += n & 1;
        n >>= 1;
    }
    return count;
}

### 3.1.2 位运算在算法中的实际应用场景
位运算在各种算法中都有广泛的应用，尤其是在需要处理大量数据、执行大量计算的场景中。

- **排序算法**：位运算可以用来实现一些高效的排序算法，例如基数排序。
- **搜索算法**：在一些特定条件下的搜索问题中，位运算可以用于快速匹配与检索。
- **动态规划**：在动态规划问题中，通过位运算可以更高效地更新状态。

例如，利用位运算实现快速乘除法：

// 使用位运算实现乘以2的幂次方
int multiplyBy2(int n) {
    return n << 1; // 等价于 n * 2
}

// 使用位运算实现除以2的幂次方
int divideBy2(int n) {
    return n >> 1; // 等价于 n / 2
}

## 3.2 位运算与数据结构
数据结构是组织数据以便于使用的抽象数据类型。位运算可以用来优化特定的数据结构操作，尤其是在数据量较大时。

### 3.2.1 位集合与位向量
位集合是一种基于位运算的数据结构，常用于快速查找和更新数据。位向量，也称为位数组，是一种用位来表示多个状态的数据结构。

- **位集合**：可以用来存储集合类型的元素，通过位的0和1表示元素的不在或在集合中。
- **位向量**：利用位向量可以有效地进行集合的并、交、补等操作。

示例代码，使用位集合实现集合的并操作：

// 假设有两个集合，通过位集合表示为两个整数
int set1 = 0b1010; // 集合 {1, 3}
int set2 = 0b0111; // 集合 {1, 2, 3}

// 集合并集
int unionSet = set1 | set2; // 结果为 0b1111

### 3.2.2 利用位运算优化数据结构操作
对于数据结构的操作，位运算提供了一种高效的方式来处理数据，特别是