单片机温度控制算法优化指南：提升精度与响应速度

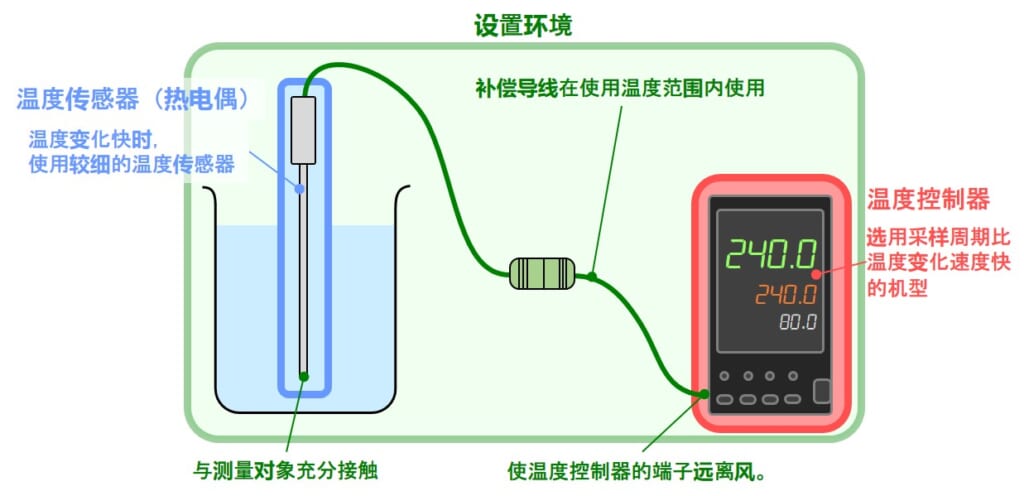
# 1. 温度控制算法概述

温度控制算法是一种用于调节和维持系统温度的算法。它广泛应用于工业、医疗和家庭自动化等领域。温度控制算法的目的是通过传感器测量系统温度，并根据预设目标温度和当前温度之间的偏差，计算出适当的控制动作，以调节加热或冷却设备，从而达到和维持所需的温度。

温度控制算法的类型有很多，每种算法都有其独特的优点和缺点。常见的温度控制算法包括比例积分微分 (PID) 控制、模糊控制、自适应控制和神经网络控制。选择合适的温度控制算法取决于系统的具体要求，如响应时间、稳定性、精度和成本。

# 2. 算法优化理论**

**2.1 PID控制原理与优化**

**2.1.1 PID参数的调优方法**

PID（比例-积分-微分）控制是一种经典的反馈控制算法，广泛应用于温度控制系统。PID参数的调优对系统性能至关重要，常用的调优方法包括：

* **Ziegler-Nichols方法：**基于系统阶跃响应的经验公式，快速获得初始PID参数。
* **Cohen-Coon方法：**基于系统传递函数的近似模型，计算出PID参数。
* **自适应调优方法：**在线调整PID参数，以适应系统参数的变化和干扰。

**代码块：**

def pid_tune_zn(kp, ki, kd, pv, sp):
    """
    Ziegler-Nichols PID参数调优方法

    Args:
        kp: 比例增益
        ki: 积分增益
        kd: 微分增益
        pv: 过程变量
        sp: 给定值

    Returns:
        调优后的PID参数
    """

    # 计算过程增益和时间常数
    ku = (pv - sp) / kp
    tau = -kd / ki

    # 根据过程类型选择调优参数
    if tau < 0.5:
        return kp * 0.6, ki * 0.4, kd * 0.3
    elif tau < 1:
        return kp * 0.8, ki * 0.6, kd * 0.4
    elif tau < 2:
        return kp * 1.0, ki * 0.8, kd * 0.5
    else:
        return kp * 1.2, ki * 1.0, kd * 0.6

**逻辑分析：**

该代码块实现了Ziegler-Nichols PID参数调优方法。首先计算过程增益和时间常数，然后根据过程类型选择调优参数。

**参数说明：**

* `kp`：比例增益
* `ki`：积分增益
* `kd`：微分增益
* `pv`：过程变量
* `sp`：给定值

**2.1.2 自适应PID算法**

自适应PID算法可以根据系统参数的变化和干扰在线调整PID参数。常用的自适应PID算法包括：

* **模糊自适应PID算法：**利用模糊推理来调整PID参数。
* **神经网络自适应PID算法：**利用神经网络来学习和预测系统参数。
* **遗传算法自适应PID算法：**利用遗传算法来优化PID参数。

**表格：**

| 自适应PID算法 | 优点 | 缺点 |
|---|---|---|
| 模糊自适应PID | 鲁棒性强，易于实现 | 计算量大 |
| 神经网络自适应PID | 学习能力强，精度高 | 训练时间长 |
| 遗传算法自适应PID | 全局搜索能力强，鲁棒性好 | 计算量大，收敛速度慢 |

**2.2 模糊控制原理与优化**

**2.2.1 模糊推理系统的设计**

模糊推理系统（FIS）是一种基于模糊逻辑的控制系统。FIS的设计包括：

* **模糊变量定义：**确定系统输入和输出的模糊变量及其取值范围。
* **模糊规则生成：**根据专家知识或数据建立模糊规则库。
* **模糊推理：**根据模糊规则和输入模糊值，推导出输出模糊值。

**代码块：**

import skfuzzy as fuzz

# 定义模糊变量
temp = fuzz.Antecedent(np.arange(0, 101, 1), 'temperature')
comfort = fuzz.Consequent(np.arange(0, 101, 1), 'comfort')

# 定义模糊集
temp['cold'] = fuzz.trapmf(temp.universe, [0, 0, 20, 30])
temp['warm'] = fuzz.trapmf(temp.universe, [20, 30, 50, 60])
temp['hot'] = fuzz.trapmf(temp.universe, [50, 60, 100, 100])

comfort['uncomfortable'] = fuzz.trapmf(comfort.universe, [0, 0, 20, 30])
comfort['comfortable'] = fuzz.trapmf(comfort.universe, [20, 30, 50, 60])
comfort['too_warm'] = fuzz.trapmf(comfort.universe, [50, 60, 100, 100])

**逻辑分析：**

该代码块使用skfuzzy库定义了模糊变量和模糊集，为模糊推理系统提供了基础。

**参数说明：**

* `temp`：模糊变量，表示温度
* `comfort`：模糊变量，表示舒适度
* `temp.universe`：温度的取值范围
* `comfort.universe`：舒适度的取值范围

**2.2.2 模糊控制器的参数优化**

模糊控制器的参数优化包括：

* **模糊规则优化：**调整模糊规则库中的规则，以提高控制器的性能。
* **模糊集优化：**调整模糊集的形状和位置，以提高控制器的鲁棒性和精度。
* **推理机制优化：**选择合适的推理机制，以提高控制器的效率和准确性。

**流程图：**

graph LR
subgraph 模糊控制器参数优化
    A[模糊规则优化] --> B[模糊集优化]
    B --> C[推理机制优化]
end

# 3. 算法优化实践

### 3.1 PID算法优化实例

#### 3.1.1 Ziegler-Nichols方法

Ziegler-Nichols方法是一种经典的PID参数调优方法，适用于稳定的一阶或二阶系统。该方法通过对系统进行阶跃响应测试，根据响应曲线的特征来确定PID参数。

**步骤：**

1. 将系统置于开环状态，施加一个阶跃输入。
2. 记录系统输出的响应曲线。
3. 根据响应曲线的特征确定以下参数：
- 延迟时间（Td）：阶跃输入后，系统输出开始变化的时间。
- 上升时间（Tu）：系统输出从10%上升到90%所需的时间。
- 稳态增益（Ku）：系统输出稳定后的值。

**参数计算：**

根据响应曲线的特征，PID参数可以按如下公式计算：

Kp = 0.6 * Ku * (Tu / Td)
Ti = 0.5 * Tu
Td = 0.125 * Tu

**代码示例：**

import control

# 定义系统传递函数
G = control.TransferFunction([1], [1, 2, 1])

# 施加阶跃输入
t, y = control.step_response(G)

# 计算响应曲线的特征
Td = t[y >= 0.1 * max(y)][0]
Tu = t[y >= 0.9 * max(y)][0] - Td
Ku = max(y)

# 计算PID参数
Kp = 0.6 * Ku * (Tu / Td)
Ti = 0.5 * Tu
Td = 0.125 * Tu

print("PID参数：")
print("Kp:", Kp)
print("Ti:", Ti)
print("Td:", Td)

**逻辑分析：**

该代码首先定义了系统的传递函数，然后施加阶跃输入并记录系统输出的响应曲线。接下来，代码计算响应曲线的特征（延迟时间、上升时间、稳态增益），并根据Ziegler-Nichols公式计算PID参数。

#### 3.1.2 Cohen-Coon方法

Cohen-Coon方法也是一种常用的PID参数调优方法，适用于稳定的一阶或二阶系统。该方法通过对系统进行阶跃响应测试，根据响应曲线的斜率来确定PID参数。

**步骤：**

1. 将系统置于开环状态，施加一个阶跃输入。
2. 记录系统输出的响应曲线。
3. 根据响应曲线的斜率确定以下参数：
- 延迟时间（Td）：阶跃输入后，系统输出开始变化的时间。
- 上升时间（Tu）：系统输出从10%上升到90%所需的时间。
- 稳态增益（Ku）：系统输出稳定后的值。
- 响应曲线的斜率（m）：系统输出上升阶段的斜率。

**参数计算：**

根据响应曲线的斜率，PID参数可以按如下公式计算：

Kp = 1.2 * Ku / m
Ti = 2 * Td
Td = Tu / 8

**代码示例：**

import control

# 定义系统传递函数
G = control.TransferFunction([1], [1, 2, 1])

# 施加阶跃输入
t, y = control.step_response(G)

# 计算响应曲线的特征
Td = t[y >= 0.1 * max(y)][0]
Tu = t[y >= 0.9 * max(y)][0] - Td
Ku = max(y)

# 计算响应曲线的斜率
m = (y[10] - y[0]) / (t[10] - t[0])

# 计算PID参数
Kp = 1.2 * Ku / m
Ti = 2 * Td
Td = Tu / 8

print("PID参数：")
print("Kp:", Kp)
print("Ti:", Ti)
print("Td:", Td)

**逻辑分析：**

该代码与Ziegler-Nichols方法类似，但它通过计算响应曲线的斜率来确定PID参数。斜率越大，表示系统响应越快，需要的PID参数就越小。

# 4.1 温度控制系统设计

### 4.1.1 传感器选择与信号处理

温度控制系统的传感器选择至关重要，它直接影响系统的精度和稳定性。常用的温度传感器包括：

- **热电偶：**高精度、宽量程，但需要冷端补偿。
- **热敏电阻：**低成本、响应速度快，但非线性较大。
- **红外传感器：**非接触式测量，但受环境因素影响较大。

信号处理是传感器输出信号的处理过程，目的是消除噪声、校准和放大信号。常见的信号处理技术包括：

- **滤波：**去除噪声，如低通滤波器或卡尔曼滤波器。
- **校准：**补偿传感器误差，如使用标准温度源进行校准。
- **放大：**放大信号幅度，提高信噪比。

### 4.1.2 执行器控制与反馈机制

执行器是控制系统中执行控制动作的装置，在温度控制系统中，执行器通常是加热器或冷却器。

反馈机制是控制系统中将输出信号反馈给输入信号的机制，以实现闭环控制。常见的反馈机制包括：

- **负反馈：**将输出信号与设定值进行比较，并产生一个误差信号，用于控制执行器动作，以减小误差。
- **正反馈：**将输出信号与设定值进行比较，并产生一个与误差信号同向的信号，用于控制执行器动作，以增大误差。

**温度控制系统框图：**

graph LR
subgraph 传感器
    A[传感器]
    B[信号处理]
end
subgraph 控制器
    C[控制器]
end
subgraph 执行器
    D[执行器]
end
A --> B
B --> C
C --> D
D --> A

**参数说明：**

- 传感器：温度传感器，负责测量温度。
- 信号处理：信号处理模块，负责滤波、校准和放大信号。
- 控制器：温度控制器，负责计算控制信号。
- 执行器：执行器，负责执行控制信号，如加热或冷却。

**逻辑分析：**

温度控制系统是一个闭环控制系统，通过反馈机制将输出信号反馈给输入信号，实现对温度的控制。传感器测量温度，信号处理模块处理信号，控制器计算控制信号，执行器执行控制信号，最终控制温度。

# 5.1 优化算法的优缺点对比

**PID算法**

**优点：**
- 结构简单，易于实现
- 参数调优方法成熟
- 鲁棒性强

**缺点：**
- 优化效果受参数设置影响较大
- 难以处理非线性系统
- 响应速度慢

**模糊算法**

**优点：**
- 可处理非线性系统
- 响应速度快
- 鲁棒性较好

**缺点：**
- 规则库设计复杂
- 参数优化难度大
- 难以保证控制精度

**优化算法对比**

| 特征 | PID算法 | 模糊算法 |
|---|---|---|
| 结构 | 简单 | 复杂 |
| 优化难度 | 适中 | 困难 |
| 响应速度 | 慢 | 快 |
| 鲁棒性 | 强 | 较好 |
| 适用性 | 线性系统 | 非线性系统 |

## 5.2 未来算法优化方向

随着技术的发展，温度控制算法优化将朝着以下方向发展：

- **自适应算法：**实时调整参数以适应系统变化
- **智能算法：**利用机器学习和人工智能技术优化算法
- **分布式算法：**在多传感器和多执行器系统中优化控制
- **鲁棒算法：**提高算法在干扰和不确定性下的稳定性
- **节能算法：**优化算法以降低能耗