【高性能计算算法选择】：空间复杂度在科学计算中的重要性

# 1. 高性能计算算法概述

在探讨高性能计算领域时，算法是核心要素之一。高性能计算（High-Performance Computing, HPC）算法关注于如何使用有限的计算资源在最短时间内完成复杂计算任务。本章主要目的是提供对高性能计算算法的初步认识，并为后续章节的深入分析打下基础。

## 1.1 算法在高性能计算中的地位

算法是解决问题的具体步骤和方法，它规定了计算机如何通过一系列操作从输入得到输出。在高性能计算场景中，算法的选择和设计直接关联到计算效率、资源使用和系统稳定性。

## 1.2 高性能计算的应用场景

高性能计算的应用广泛，如科学研究、天气预报、生物信息学、金融分析等领域，都需要依赖复杂的算法来处理海量数据和进行大规模模拟。

## 1.3 算法性能的衡量指标

衡量算法性能的关键指标包括时间复杂度和空间复杂度。时间复杂度关注算法的运行时间，而空间复杂度关注算法在运行过程中占用的存储空间。本系列文章将重点探讨空间复杂度的优化。

在接下来的章节中，我们将深入探讨空间复杂度的理论基础和优化实践，从而引导读者掌握在高性能计算场景中，如何通过算法优化来提高系统性能。

# 2. 空间复杂度的理论基础

在现代计算领域，算法的空间复杂度评估变得尤为重要。空间复杂度指的是在算法执行过程中所需存储空间的大小，这包括了算法执行过程中需要的所有变量、数据结构、函数调用栈等。它不仅与输入数据的大小有关，还与算法的实现细节紧密相关。理解空间复杂度的定义和分析是开发高效算法的第一步。

## 2.1 空间复杂度定义

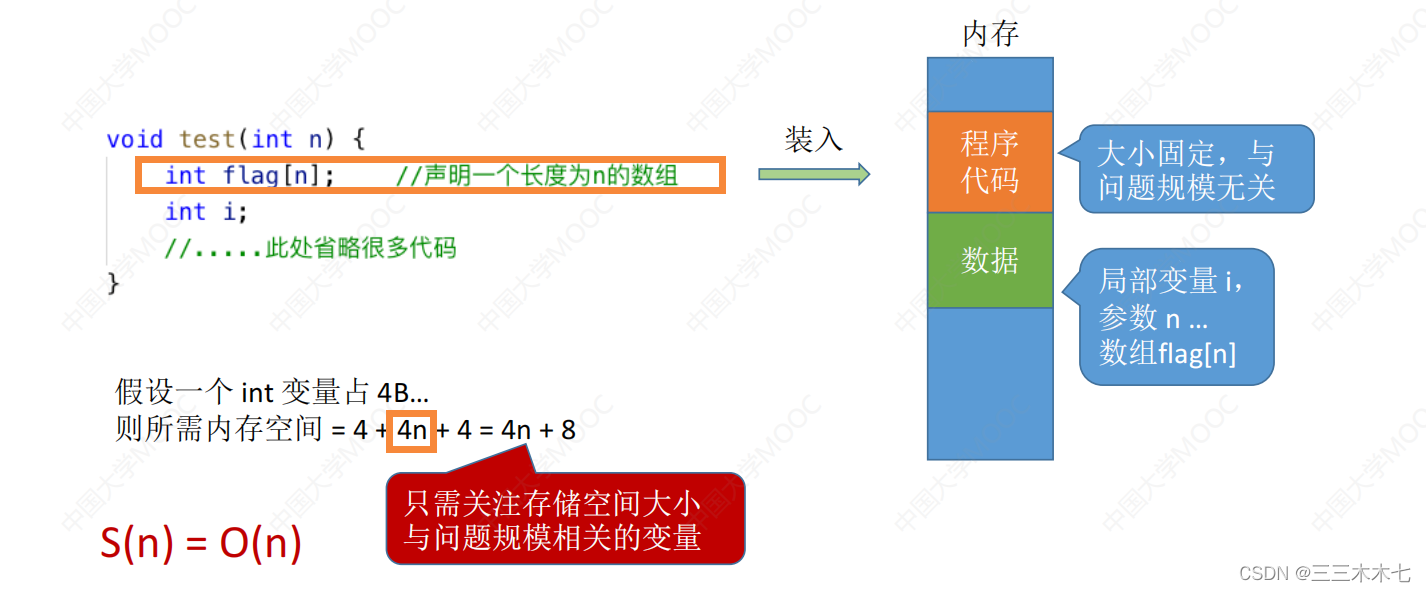
### 2.1.1 空间复杂度的计算方法

空间复杂度通常用大O符号进行表示，如O(1)、O(n)、O(n^2)等。这些表示法描述了随着输入数据大小增加，算法所需空间的增长趋势。空间复杂度分为两种：固定空间复杂度和额外空间复杂度。

- **固定空间复杂度**：指的是算法执行过程中始终占用且不随输入大小变化的空间。例如，如果一个算法仅使用了常数个变量，那么它的固定空间复杂度为O(1)。
- **额外空间复杂度**：指的是除了输入数据占用的空间外，算法执行过程中需要的额外空间。例如，一个算法在排序时创建了一个与输入数据等长的辅助数组，那么这个算法的额外空间复杂度为O(n)。

计算空间复杂度的一个实用方法是遍历算法的伪代码，统计所有变量和数据结构占用的空间，并根据它们的大小进行分类。

### 2.1.2 空间复杂度与其他复杂度的关系

空间复杂度和时间复杂度是算法效率的两个重要衡量指标。两者通常需要权衡，一个高效的算法需要在时间和空间复杂度上都取得良好的平衡。在一些情况下，可以通过增加额外空间来减少时间复杂度（例如使用哈希表减少查找时间），而在其他情况下，减少空间使用可能意味着更长的执行时间。

## 2.2 空间复杂度分析的重要性

### 2.2.1 空间效率对性能的影响

空间效率直接关系到程序运行的性能和资源占用。一个空间效率低的算法可能会占用大量内存资源，导致内存泄漏、垃圾回收频繁等性能问题。在资源受限的环境中（如嵌入式系统、移动设备），空间效率尤其重要。此外，对于需要处理大规模数据的应用，空间复杂度会直接影响到算法的可扩展性。

### 2.2.2 优化空间复杂度的现实意义

在实际应用中，优化空间复杂度具有以下几个现实意义：
- **减少硬件成本**：高效的空间利用意味着更少的内存需求，这可能会降低硬件成本。
- **提高系统性能**：优化空间复杂度可以减少内存访问延迟，提高缓存命中率，从而提高整体系统性能。
- **增强可扩展性**：在处理大规模数据集时，空间效率高的算法更容易扩展到多台机器上，对于大数据处理尤其重要。

在接下来的章节中，我们将具体探讨如何在实践中优化空间复杂度，并分析数据结构选择、算法实现等对空间复杂度的具体影响。

# 3. 空间复杂度优化实践

## 3.1 存储结构选择与优化
### 3.1.1 数据结构对空间复杂度的影响

在讨论数据结构对空间复杂度的影响之前，首先要理解数据结构的基本概念。数据结构是一门研究数据组织、存储方式和数据操作方法的学科。不同的数据结构占用的存储空间不同，执行数据操作的效率也各异。选择合适的数据结构，对于优化程序的空间复杂度至关重要。

例如，数组是一种基本的数据结构，它占用连续的内存空间，因此在访问元素时速度较快，但在插入和删除元素时可能会因为移动大量元素而导致效率低下。相比之下，链表虽然插入和删除操作效率较高，但每个节点需要额外的空间来存储指针，因此总体占用的空间比数组要大。

在选择数据结构时，应根据问题的具体需求，权衡不同操作的频率和重要性，从而选择对空间复杂度最优化的数据结构。

// 示例：数组与链表的空间复杂度比较
struct Node {
    int data;
    struct Node* next;
};

如上所示，链表的每个节点包含数据和指向下一个节点的指针，而数组则不需要额外的指针空间，但是数组的插入和删除操作会导致大量元素移动。根据实际场景，开发者可以选择更适合的数据结构，以达到空间优化的目的。

### 3.1.2 常见数据结构的空间优化技巧

优化数据结构的空间使用是算法工程师经常面对的问题。在许多情况下，优化的空间复杂度可以带来性能的提升，尤其是在处理大规模数据时。

- **稀疏矩阵的压缩存储**: 在许多应用中，如图像处理和科学计算，可能会遇到大量的零元素，这种矩阵被称为稀疏矩阵。为了节省空间，可以采用压缩存储技术，如行压缩存储（CRS）、列压缩存储（CCS）或者块存储（BSR）等。

- **哈希表的动态扩容**: 哈希表是键值对的集合，为了处理哈希冲突，它们通常使用链表或开放寻址法。然而，哈希表的空间使用与其负载因子相关。通过动态扩容技术，可以调整表的大小，维持较低的负载因子，从而实现空间的优化利用。

// 示例：哈希表的动态扩容机制
#define INITIAL_SIZE 16
#define LOAD_FACTOR 0.75

typedef struct HashTableEntry {
    int key;
    int value;
    struct HashTableEntry *next;
} HashTableEntry;

typedef struct HashTable {
    HashTableEntry **buckets;
    int size;
    int capacity;
} HashTable;

void resizeHashTable(HashTable *table) {
    // 逻辑说明：当哈希表负载因子超过LOAD_FACTOR时，扩容两倍并