【Java算法优化】：深入分析数组转字符串的时间复杂度

# 1. 时间复杂度与算法优化基础

## 1.1 理解时间复杂度
时间复杂度是衡量算法运行效率的一种度量方式。它主要描述了随着输入规模的增长，算法执行所需时间的增加趋势。理解时间复杂度的基本概念，对于编写高效的代码至关重要。

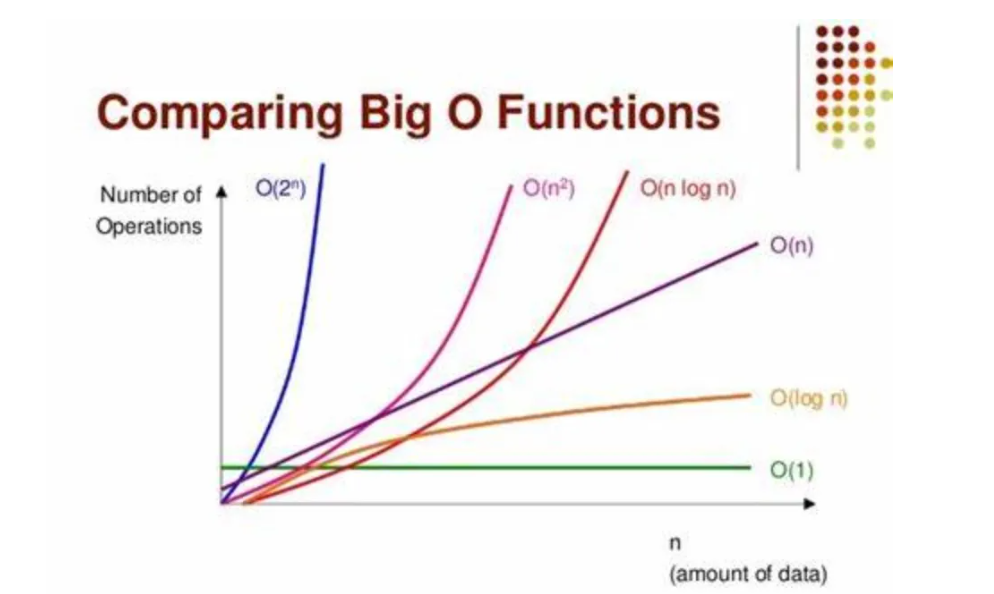
## 1.2 大O表示法
大O表示法用于描述算法性能的上界，表示在最坏情况下的时间复杂度。常见的时间复杂度包括O(1)、O(log n)、O(n)、O(n log n)、O(n^2)等。O(1)是最优的，代表算法执行时间不随输入规模变化。

## 1.3 算法优化的重要性
在IT领域，算法优化可以显著提升程序性能，减少计算资源的消耗。了解如何分析和优化算法的时间复杂度，对提高软件运行效率和用户体验具有重要意义。

# 2. Java数组操作与时间复杂度分析

## 2.1 Java数组的基本操作

### 2.1.1 数组的声明与初始化

在Java中，数组是一种数据结构，它可以存储固定大小的同类型元素。声明一个数组需要指定数组类型以及数组中的元素数量。初始化数组可以通过直接赋值，也可以使用数组初始化器。

int[] numbers = new int[10]; // 声明并初始化一个包含10个整数的数组

数组初始化还可以在声明时完成：

int[] numbers = {1, 2, 3, 4, 5}; // 使用数组初始化器直接声明并初始化数组

这种声明方式在数组元素已知且数组大小固定时非常有用。值得注意的是，数组一旦被初始化，其大小就不可改变。若需要动态改变数组大小，可以考虑使用`ArrayList`等集合类。

### 2.1.2 数组元素的访问与修改

数组的元素可以通过索引访问。在Java中，数组索引从0开始。访问数组元素时，若索引超出数组界限，Java将抛出`ArrayIndexOutOfBoundsException`。

int number = numbers[0]; // 访问数组第一个元素
numbers[1] = 100; // 修改数组第二个元素为100

修改数组元素的值是一个时间复杂度为O(1)的操作，因为数组是连续存储的。这种特性在需要频繁读写单个元素的场景下非常有用。

## 2.2 Java数组遍历的时间复杂度

### 2.2.1 线性遍历的时间复杂度

线性遍历是数组遍历中最常见的方式，对于一维数组而言，其时间复杂度为O(n)，其中n为数组的长度。这种遍历方式简单且高效，适用于大多数情况。

for (int i = 0; i < numbers.length; i++) {
    System.out.println(numbers[i]); // 线性遍历数组并打印每个元素
}

### 2.2.2 高效遍历算法介绍

当需要频繁遍历数组且对性能有更高要求时，可以考虑一些优化策略。比如对于部分特定的应用场景，可以使用并行遍历的方式利用多核处理器加速处理过程。然而，并行处理涉及多线程编程，需要注意线程安全问题以及可能带来的额外开销。

## 2.3 多维数组遍历与时间复杂度

### 2.3.1 常规遍历方法的复杂度分析

多维数组的遍历相对复杂一些，通常涉及嵌套循环。对于一个二维数组，其遍历的时间复杂度依然是O(n)，但n变成了二维数组中元素的总数。

for (int i = 0; i < matrix.length; i++) {
    for (int j = 0; j < matrix[i].length; j++) {
        System.out.println(matrix[i][j]); // 遍历二维数组并打印每个元素
    }
}

对于三维数组或更高维度的数组，时间复杂度和嵌套循环的层数成正比。

### 2.3.2 优化策略及其实现

对于多维数组的遍历，一种常见的优化策略是减少不必要的操作，例如在循环内部避免重复计算长度，或者在满足某些条件时提前退出循环，减少迭代次数。

## 表格示例

为了更好地理解多维数组的遍历，我们制作了一个简单的表格，展示了不同维度数组的遍历时间和空间开销。

| 数组维度 | 时间复杂度 | 空间开销 | 遍历方法 |
|----------|------------|----------|----------|
| 一维 | O(n) | O(1) | 线性遍历 |
| 二维 | O(n*m) | O(1) | 双层循环 |
| 三维 | O(n*m*p) | O(1) | 三层循环 |

其中，n、m、p分别代表数组在各个维度上的大小。需要注意的是，空间开销是针对单个数组元素来说的，因此这里都是O(1)，因为数组元素大小是固定的。

## Mermaid 流程图示例

在介绍Java数组遍历的时间复杂度时，一个流程图有助于展示遍历的逻辑流程。这里是一个简化的流程图，用于表示二维数组遍历的逻辑：

graph TD
    A[开始] --> B[外层循环: 行i]
    B --> C[内层循环: 列j]
    C --> D[访问matrix[i][j]]
    D --> E{列j结束?}
    E -- 是 --> F[列i+1]
    F --> C
    E -- 否 --> C
    F --> G{行i结束?}
    G -- 是 --> H[结束]
    G -- 否 --> B

## 代码块示例

为了进行多维数组的遍历优化，可以使用以下代码块，采用部分遍历和早期退出的策略：

for (int i = 0; i < matrix.length; i++) {
    for (int j = 0; j < matrix[i].length; j++) {
        // 某些特定条件判断
        if (shouldExit(matrix[i][j])) {
            break; // 满足条件，跳出内层循环
        }
        System.out.println(matrix[i][j]);
    }
    if (shouldExit(matrix[i])) {
        break; // 满足条件，跳出外层循环
    }
}