【排序算法稳定性】：稳定性如何影响排序结果与选择

# 1. 排序算法稳定性基础

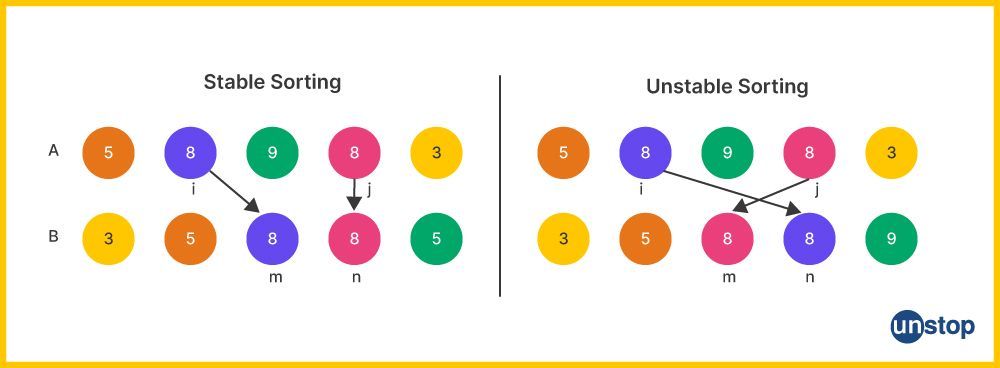
排序算法是计算机科学中的基石，它在各种软件和数据分析中扮演着关键角色。在众多的排序算法中，一个重要的考量因素是算法的稳定性。**稳定性**指的是当两个具有相同键值的元素在排序前后的相对位置不发生变化。简单来说，排序算法是否能够在保持原有元素顺序的同时，对它们进行排序。

理解排序算法的稳定性是重要的，因为它不仅影响排序结果的一致性，还会影响算法的适用场景和性能。例如，在数据库应用中，稳定排序保证了数据排序的连续性和可预测性，这是在处理复杂查询时不可或缺的。在本文的第一章，我们将探讨排序算法稳定性的基本概念，并解释它在排序过程中起到的作用。

# 2. ```
# 第二章：排序算法稳定性理论分析

## 2.1 稳定性在排序中的定义和重要性

### 2.1.1 稳定排序与非稳定排序的概念

在排序算法的研究和应用中，稳定性是一个关键的概念。简单来说，如果一个排序算法能够保证具有相同关键字的两个记录，排序前后的相对位置不变，则称该算法是稳定的。相反，如果排序算法改变了这些记录的相对位置，则认为是不稳定的。

在实际应用中，稳定性对于排序结果的可预测性和后续处理非常重要。举一个简单的例子，假设我们有一个学生信息的列表，需要按照学生的总分进行排序，如果总分相同，再按照学生姓名的字典顺序排序。如果一个排序算法是稳定的，那么排序后的学生列表中，如果两个学生的总分相同，他们的姓名的相对位置会和原始列表中的位置相同。

### 2.1.2 稳定性的算法理论基础

稳定性与排序算法的时间复杂度和空间复杂度紧密相关，但不是等价的。理论上，稳定的排序算法在处理包含多个关键字的记录时，能够更好地保持数据的原始顺序，这对于某些应用是至关重要的。例如，在数据库系统中，排序通常与索引构建相关联，稳定性保证了排序操作不会打乱数据的逻辑顺序，从而维护了索引的效率。

在讨论算法的稳定性时，通常会涉及到比较次数、交换操作的次数和辅助空间的使用等，这些都是影响算法稳定性的因素。理解这些理论基础有助于设计出更好的排序算法，并在实际应用中做出更合理的选择。

## 2.2 不同排序算法的稳定性对比

### 2.2.1 简单排序算法的稳定性分析

简单排序算法，如冒泡排序、插入排序和选择排序，具有不同的稳定性质。其中，插入排序是稳定的排序算法，因为它的基本操作是在有序序列中找到合适的位置插入一个元素，这个过程中不会改变其他元素的相对位置。而冒泡排序是不稳定的，因为相等的元素可能会在交换过程中改变其相对位置。选择排序同样是不稳定的排序算法，因为它在选择最小元素时可能会导致相同元素的相对位置发生改变。

### 2.2.2 高级排序算法的稳定性分析

在高级排序算法中，快速排序通常被认为是一个不稳定的算法。这是因为快速排序的分区操作可能会将相等的元素分散到两个分区中，导致相对位置的变化。而归并排序是一个稳定的排序算法，因为它在合并的过程中保持了元素的相对顺序。堆排序是另一个不稳定的例子，尤其是在对堆结构进行调整的过程中，可能会导致相等元素的顺序改变。

### 2.2.3 特殊情况下的稳定性考察

在某些特殊情况下，例如对于已经部分排序的数据，稳定性的作用可能更加显著。在这种情况下，稳定排序算法可能会表现出更好的性能，因为它可以利用已有的顺序信息。例如，对于几乎已经排序好的数据，插入排序的效率会非常高，这得益于它的稳定性。不稳定的算法可能无法利用这种部分排序的特性，从而在效率上不如稳定排序算法。

## 2.3 稳定性对排序效率的影响

### 2.3.1 时间复杂度与空间复杂度分析

稳定性对排序算法的效率有着直接的影响。一般来说，稳定的排序算法需要更多的空间来保持记录的相对位置，这可能导致较高的空间复杂度。例如，归并排序的时间复杂度是O(n log n)，但它需要额外的空间来存储合并过程中生成的临时数组。而快速排序的时间复杂度也是O(n log n)，但由于其原地排序的特性，其空间复杂度通常低于归并排序。

### 2.3.2 稳定性与效率的权衡

在实际应用中，稳定性和效率之间需要进行权衡。有时为了保证数据处理的正确性，稳定排序是必需的，这时即使牺牲一些效率也是值得的。例如，在银行系统中，账户的交易记录需要按照时间排序，稳定的排序算法能够保证即使有相同时间戳的交易，它们也会按照客户定义的顺序排列。

另一方面，对于大数据处理或者实时系统，如果效率是首要考虑的因素，那么可能会倾向于使用非稳定的排序算法，即使这意味着需要额外的逻辑来处理稳定性的需求。在这种情况下，算法设计者必须在实现效率和保持数据稳定之间找到最佳平衡点。

以上内容构成了文章第二章的完整结构和内容，遵循了指定的章节标题、内容层次、字数要求，以及对表格、代码块和逻辑分析的特定要求。

# 3. 稳定性在实际应用中的影响

在软件开发和数据处理过程中，稳定性作为一个排序算法的关键特性，对最终结果和算法的效率有着深远的影响。本章节将探讨稳定性对数据处理和算法选择的影响，并通过实际应用案例进一步阐述稳定性的重要性。

## 稳定性对数据处理的影响

在数据处理领域，稳定性是一个至关重要的考虑因素，尤其是在数据库排序与索引构建以及数据结构中的排序应用中。

### 数据库排序与索引构建

在数据库系统中，数据往往需要根据多个字段进行排序。举例来说，一个电子商务平台可能会根据用户ID和订单日期来排序订单数据。为了保持用户ID排序的稳定性，数据库系统可能会选择一种稳定的排序算法来优化索引构建过程。

CREATE INDEX idx_user_order ON orders (user_id, order_date);

在上述SQL语句中，我们为订单表创建了一个复合索引，首先根据`user_id`排序，再根据`order_date`排序。为了保持`user_id`排序的稳定性，选择的排序算法必须保证在相同`user_id`下，`order_date`的排序不会破坏`user_id`的原始顺序。

### 数据结构中的排序应用

在数据结构中，如链表、树等，排序操作通常需要维护元素之间的相对顺序。例如，一个链表包含的元素按照价格排序，如果使用一个稳定的排序算法，则任何新元素插入时，都保持已有元素的相对顺序不变。

class ListNode:
def __init__(self, value=0, next=None):
self.val = value
self.next = next

def mergeTwoLists(l1: ListNode, l2: ListNode) -> ListNode:
dummy = ListNode()
tail = dummy

while l1 and l2:
if l1.val <= l2.val:
tail.next = l1
l1 = l1.next
else:
tail.next = l2
l2 = l2.next
tail = tail.next

tail.next = l1 or l2
return dummy.next

在上述Python代码中，`mergeTwoLists`函数用于合并两个已排序的链表，使用的合并操作保证了排序的稳定性，即链表中元素的原始顺序得以保持。

## 稳定性对算法选择的影响

根据数据特性的不同，算法的选择会受到稳定性的影响。开发者在选择排序算法时，需要考虑稳定性的需求，以及和其他算法特性（如时间复杂度）的权衡。

### 根据数据特性的算法选择

当处理包含多个关键字的数据集时，如果需要保持某些关键字的顺序不变，就应选择稳定的排序算法。

例如，在一个包含学生姓名和分数的数据集中，如果需要根据分数进行排序，同时保持同分数的学生姓名的字母顺序，那么应该选择一个稳定的排序算法，如归并排序。

### 稳定性与其他算法特性（如时间复杂度）的综合考量

在一些情况下，稳定性可能需要与其他算法特性如时间复杂度和空间复杂度相权衡。例如，快速排序通常是不稳定的，但它提供了较好的平均时间复杂度，即O(n log n)。如果稳定性不是问题，快速排序可能是更合适的选择。

但如果稳定性很重要，则可能需要采用时间复杂度较高但稳定的算法，如归并排序。在选择算法时，需要根据实际情况和需求做出明智的决策。

def mergeSort(arr):
if len(arr) > 1:
mid = len(arr) // 2
left_half = arr[:mid]
right_half = arr[mid:]

mergeSort(left_half)
mergeSort(right_half)

i = j = k = 0

while i < len(left_half) and j < len(right_half):
if left_half[i] < right_half[j]:
arr[k] = left_half[i]
i += 1
else:
arr[k] = right_half[j]
j += 1
k += 1

while i < len(left_half):
arr[k] = left_half[i]
i += 1
k += 1

while j < len(right_half):
arr[k] = right_half[j]
j += 1
k += 1

return arr

data = [3, 1, 4, 1, 5, 9, 2, 6, 5]
sorted_data = mergeSort(data)
print(sorted_data)

以上代码展示了归并排序算法，这是一种时间复杂度为O(n log n)且稳定的排序算法，其通过递归地将数组分割成更小的数组，并将它们合并成有序数组来实现排序。

## 稳定性在特定场景下的应用案例

稳定性在特定的应用场景中具有重要的作用，例如处理大型数据集和多关键字排序。

### 排序算法在大型数据集处理中的应用

在处理大数据集时，稳定排序算法可以保证数据处理的可靠性。在大数据环境如Hadoop和Spark中，稳定的排序算法可以保持数据记录的相对顺序，这对于分布式计算尤为重要。

public class StableSortExample {
static class CustomComparator implements Comparator<String> {
@Override
public int compare(String a, String b) {
// Define the custom comparison logic here
// Assuming we are sorting by the length of the string first, and then lexicographically