【性能对比分析】：排序算法的最坏与平均情况性能比较

# 1. 排序算法的理论基础

排序算法是计算机科学中不可或缺的一部分，它们是组织和管理数据的关键工具。在深入探讨各种排序算法之前，了解排序算法的理论基础至关重要。

## 1.1 排序算法的定义与目的

排序算法的目的是将一组数据按照特定顺序重新排列。排序可以是升序也可以是降序，具体取决于应用场景的需求。排序的基本操作是交换、比较和移动数据项。

## 1.2 排序算法的基本分类

排序算法可以大致分为两类：比较排序和非比较排序。比较排序通过比较元素间的大小关系来排序，而非比较排序则不直接通过比较来实现排序，例如计数排序和基数排序。

## 1.3 算法性能的关键指标

性能评估是衡量排序算法效率的重要方面，主要关注三个指标：时间复杂度、空间复杂度和稳定性。时间复杂度关注算法执行所需的时间，空间复杂度关注算法执行过程中所需的额外空间，而稳定性则指的是排序后相等元素之间的相对顺序是否保持不变。

graph TD;
    A[排序算法] --> B[比较排序]
    A --> C[非比较排序]
    B --> D[时间复杂度]
    B --> E[空间复杂度]
    B --> F[稳定性]
    C --> G[计数排序]
    C --> H[基数排序]

在后续章节中，我们将进一步分析常见排序算法的性能，以及它们在不同场景下的应用。

# 2. 常见排序算法的最坏情况性能分析

排序算法在实际应用中面临着不同的数据情况，包括最坏情况、平均情况和最佳情况。最坏情况分析对于了解算法的效率和可靠性至关重要，尤其是在需要保证性能的场合。下面，我们逐一对比分析冒泡排序、选择排序、插入排序、快速排序、堆排序、归并排序和希尔排序在最坏情况下的性能。

### 2.1 冒泡排序与选择排序的性能对比

#### 2.1.1 冒泡排序的最坏情况分析

冒泡排序是一种简单直观的排序算法，它重复地遍历要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。遍历数列的工作是重复进行的，直到没有再需要交换的元素为止。其最坏情况发生在输入数组完全逆序时，即每次遍历都会产生一次交换。

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr

# 最坏情况示例
import random
random_list = list(range(10, 0, -1))
print("Original list:", random_list)
sorted_list = bubble_sort(random_list)
print("Sorted list:", sorted_list)

最坏情况下的时间复杂度为O(n^2)，这是因为冒泡排序需要进行n-1轮遍历，每轮遍历都会对最多n-i个元素进行比较和可能的交换。

#### 2.1.2 选择排序的最坏情况分析

选择排序算法选择未排序部分的最小元素，然后将其与未排序部分的第一个元素交换位置。选择排序的最坏情况发生在所有元素的相对大小顺序都相同，即每次选择最小元素时都需要遍历整个未排序部分。

def selection_sort(arr):
    for i in range(len(arr)):
        min_idx = i
        for j in range(i+1, len(arr)):
            if arr[min_idx] > arr[j]:
                min_idx = j
        arr[i], arr[min_idx] = arr[min_idx], arr[i]
    return arr

# 最坏情况示例
import random
random_list = [i for i in range(1, 11)]
print("Original list:", random_list)
sorted_list = selection_sort(random_list)
print("Sorted list:", sorted_list)

选择排序的时间复杂度无论在什么情况下都是O(n^2)，这是因为算法的两个嵌套循环结构导致的。

### 2.2 插入排序与快速排序的性能对比

#### 2.2.1 插入排序的最坏情况分析

插入排序的工作方式类似于人类整理扑克牌。它遍历数组，对于每个新元素，从后向前扫描已排序部分，然后将它插入到正确的位置。如果数组完全逆序，插入排序将退化为O(n^2)的时间复杂度。

def insertion_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i-1
        while j >=0 and key < arr[j]:
            arr[j+1] = arr[j]
            j -= 1
        arr[j+1] = key
    return arr

# 最坏情况示例
import random
random_list = list(range(10, 0, -1))
print("Original list:", random_list)
sorted_list = insertion_sort(random_list)
print("Sorted list:", sorted_list)

最坏情况下插入排序需要进行n-1次插入，每次插入可能需要移动至多n-1个元素，因此时间复杂度为O(n^2)。

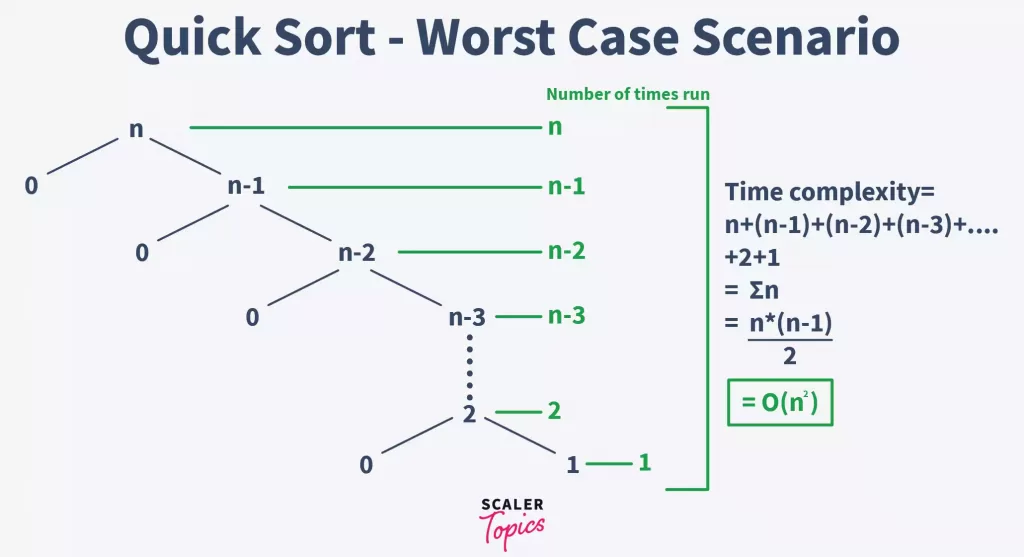
#### 2.2.2 快速排序的最坏情况分析

快速排序通过一个分区操作将要排序的数组分为两个部分，其中一部分的所有元素都比另一部分小。分区操作的最坏情况发生在每次划分都将数据分割为两个几乎相等的部分，此时递归的深度为n，每层递归需要O(n)的时间，导致最坏情况的时间复杂度为O(n^2)。

import random

def quicksort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quicksort(left) + middle + quicksort(right)

# 最坏情况示例
random_list = [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
print("Original list:", random_list)
sorted_list = quicksort(random_list)
print("Sorted list:", sorted_list)

为了改善快速排序的最坏情况，我们可以采用随机化的枢轴选择方法，以减少分区极端不平衡的几率。

### 2.3 堆排序与其他复杂排序算法的性能对比

#### 2.3.1 堆排序的最坏情况分析

堆排序是一种基于比较的排序算法，它利用堆这种数据结构进行排序。最坏情况发生在每次向下堆调整时，堆调整的时间复杂度为O(logn)，因此堆排序在最坏情况下的时间复杂度为O(nlogn)。

def heapify(arr, n, i):
    largest = i
    l = 2 * i + 1
    r = 2 * i + 2

    if l < n and arr[i] < arr[l]:
        largest = l

    if r < n and arr[largest] < arr[r]:
        largest = r

    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)

def heap_sort(arr):
    n = len(arr)

    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)

    for i in range(n-1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]
        heapify(arr, i, 0)

    return arr

# 最坏情况示例
import random
random_list = [random.randint(1, 100) for i in range(10)]
print("Original list:", random_list)
sorted_list = heap_sort(random_list)
print("Sorted list:", sorted_list)

堆排序的平均和最坏情况时间复杂度都是O(nlogn)，这是因为堆结构保证了每次插入和删除操作都能在O(logn)内完成。

#### 2.3.2 归并排序与希尔排序的最坏情况分析

归并排序和希尔排序都是在最坏情况下时间复杂度为O(nlogn)的排序算法。归并排序通过递归方式将数组分成两半进行排序，然后合并结果。希尔排序通过将原始数据分成特定间隔的子序列进行比较和交换。

def merge_sort(arr):
    if len(arr) > 1:
        mid = len(arr) // 2
        L = arr[:mid]
        R = arr[mid:]

        merge_sort(L)
        merge_sort(R)

        i = j = k = 0

        while i < len(L) and j < len(R):
            if L[i] < R[j]:
                arr[k] = L[i]
                i += 1
            else:
                arr[k] = R[j]
                j += 1
            k += 1

        while i < len(L):
            arr[k] = L[i]
            i += 1
            k += 1

        while j < len(R):
            arr[k] = R[j]
            j += 1
            k += 1
    return arr

# 归并排序示例
import random
random_list = [random.randint(1, 100) for i in range(10)]
print("Original list:", random_list)
sorted_list = merge_sort(random_list)
print("Sorted list:", sorted_li