【R语言高级数据分析必备】：plm模型性能优化实战指南

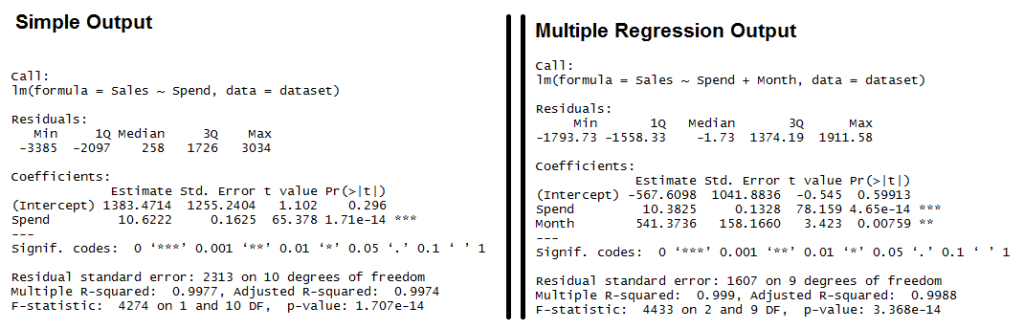
# 1. R语言与高级数据分析简介

R语言作为数据分析领域内应用广泛的编程语言之一，其强大的统计分析和图形表现能力使之成为研究者的得力助手。本章旨在为读者提供一个关于R语言及其在高级数据分析中应用的概览。

## 1.1 R语言简介
R语言是一种开源编程语言，专为统计分析和数据可视化设计。它拥有大量的包和社区支持，使得R能够适应从简单的数据处理到复杂的机器学习等多种分析任务。

## 1.2 高级数据分析概念
高级数据分析是指使用统计模型、机器学习技术等来揭示数据之间的深层次关系。本节将介绍数据科学中的核心概念，并解析如何运用R语言来解决实际问题。

## 1.3 R语言在数据分析中的优势
R语言具有高度的灵活性和可扩展性，能够快速处理大量数据，并且可以轻松地与其他语言如Python、SQL进行接口。本节将探讨R语言如何在数据分析中脱颖而出。

在这一章，我们将通过实际案例展示如何使用R语言进行基本的数据导入、清洗、变换、可视化，以及如何使用高级函数进行数据建模。为后续章节中plm模型的深入学习打下基础。

# 2. plm模型基础

## 2.1 plm模型的理论基础

### 2.1.1 固定效应模型与随机效应模型

plm模型，即面板数据模型（Panel Data Model），是用于分析具有时间序列和横截面数据的统计模型。在面板数据分析中，固定效应模型（Fixed Effects Model）和随机效应模型（Random Effects Model）是两个核心概念。

固定效应模型假设个体效应是与解释变量相关的，并且在样本期间内是不变的。这种模型适用于个体效应与解释变量之间存在相关性的情况。举个例子，如果研究的是不同公司的利润率，公司效应（比如管理质量）可能与公司的某些特征（如公司规模）相关，而且在观察期间是固定的。

随机效应模型假设个体效应与解释变量无关，并且是一个随机抽取的样本。该模型适用于个体效应是一个随机变量，且与其他解释变量不相关的情况。比如，在研究学生的学习成绩时，每个学生的个人背景（如家庭环境）可能是一个随机效应，与课程成绩没有直接相关性。

在R语言中，我们可以使用`plm`包来实现这两种模型。代码示例：

# 安装并加载plm包
install.packages("plm")
library(plm)

# 读取数据集
data("Grunfeld", package = "plm")

# 为模型构建公式
formula <- inv ~ value + capital

# 固定效应模型
fixed_effect_model <- plm(formula, data = Grunfeld, index = c("firm", "year"), model = "within")

# 随机效应模型
random_effect_model <- plm(formula, data = Grunfeld, index = c("firm", "year"), model = "random")

# 查看模型摘要
summary(fixed_effect_model)
summary(random_effect_model)

### 2.1.2 模型的适用场景分析

选择使用固定效应模型还是随机效应模型取决于数据的特点和研究的目标。在实践中，可以通过Hausman检验来决定使用固定效应模型还是随机效应模型。如果Hausman检验拒绝了随机效应模型的无偏性假设，则应该使用固定效应模型。

固定效应模型能够控制未观测到的个体异质性，适合于解释变量与个体效应相关的情形，但不能估计不随时间变化的解释变量。随机效应模型假设个体效应与解释变量不相关，可以估计不随时间变化的解释变量，但当个体效应与解释变量相关时，会导致估计偏误。

在R中实现Hausman检验的代码如下：

# Hausman检验
plmtest(fixed_effect_model, effect = "individual")

如果检验结果拒绝了随机效应模型，那么我们应该使用固定效应模型。反之，如果检验结果不能拒绝随机效应模型，则可以考虑使用随机效应模型。在某些情况下，可能需要同时考虑固定效应和随机效应模型的优缺点，并结合专业知识做出选择。

## 2.2 plm模型的构建与评估

### 2.2.1 数据准备与预处理

在构建plm模型之前，需要对数据进行彻底的检查和预处理。数据预处理包括清洗数据、处理缺失值、异常值检测、数据转换等步骤。为了确保模型的有效性，应确保数据的质量。

在R语言中，可以使用`dplyr`包来处理数据预处理任务。具体操作包括使用`filter()`来筛选数据，`mutate()`来转换变量，以及`select()`来选择数据框中的变量等。

# 安装并加载dplyr包
install.packages("dplyr")
library(dplyr)

# 数据清洗
clean_data <- Grunfeld %>%
  filter(!is.na(inv) & !is.na(value)) %>%  # 移除含有缺失值的行
  mutate(log_inv = log(inv), log_value = log(value)) %>%  # 对变量取对数
  select(firm, year, log_inv, log_value, capital)  # 选择需要的变量

# 查看清洗后的数据
head(clean_data)

### 2.2.2 模型构建的步骤与技巧

模型构建通常遵循以下步骤：

1. **数据探索**：通过图形分析、描述性统计等手段了解数据特征。
2. **模型选择**：基于数据特点选择合适的plm模型类型（固定效应或随机效应）。
3. **模型估计**：使用`plm`函数估计模型参数。
4. **模型诊断**：检查模型诊断指标，如异方差、序列相关、单位根等问题。
5. **模型修正**：根据诊断结果对模型进行修正。

在R语言中，构建plm模型的代码如下：

# 使用plm函数构建固定效应模型
fixed_effect_model <- plm(log_inv ~ log_value + capital, data = clean_data, 
                          index = c("firm", "year"), model = "within")

# 使用plm函数构建随机效应模型
random_effect_model <- plm(log_inv ~ log_value + capital, data = clean_data, 
                           index = c("firm", "year"), model = "random")

### 2.2.3 模型评估指标与方法

模型评估是检验模型适用性和预测能力的重要环节。对于plm模型，常用评估指标包括：

- **R-squared**：模型解释力的度量。
- **F-statistic**：模型整体显著性的检验。
- **Breusch-Pagan检验**：用于检验异方差性。
- **Wooldridge检验**：用于检验自相关性。
- **Hausman检验**：用于固定效应与随机效应选择。

以下是一个示例代码，展示了如何对plm模型进行评估：

# 模型评估：固定效应模型
summary(fixed_effect_model)

# 模型评估：随机效应模型
summary(random_effect_model)

# Breusch-Pagan检验
plmtest(fixed_effect_model, effect = "individual", type = "bp")

# Wooldridge检验
WooldridgeTest(fixed_effect_model)

# Hausman检验
plmtest(fixed_effect_model, effect = "individual")

在进行模型评估时，需要对每一个指标进行详细分析，以确保模型的有效性。对于面板数据模型来说，异方差性和自相关性是两个常见问题，必须通过相应的检验来确认并采取相应措施处理。这可能包括使用稳健的标准误差、变换模型或使用时间序列技术来修正。

通过本章的介绍，我们已经对plm模型有了基础的理论理解，并且通过R语言实现了模型的构建和评估。在下一章，我们将探讨如何对plm模型进行性能优化，以及如何进行模型调参和验证。这将帮助我们获得更准确、更高效的模型结果。

# 3. plm模型性能优化

随着数据分析领域的进步，优化plm（Panel Data Model）模型的性能变得越来越重要，以适应复杂多变的数据分析需求。性能优化不仅涉及算法的选择和调优，还包括对模型评估和验证的深入理解。本章节将探讨plm模型性能优化的策略，包括但不限于优化算法的选择、模型调参的策略，以及交叉验证技术的应用。

## 3.1 优化算法与技术选择

在面对复杂的数据和问题时，选择合适的优化算法是模型性能提升的关键。优化技术的应用需要根据具体的数据特点和分析需求来决定。

### 3.1.1 常用优化算法概览

优化算法可以大致分为两类：数值优化方法和启发式优化方法。数值优化方法包括梯度下降、牛顿法和拟牛顿法等，它们适用于连续可导的目标函数。启发式优化方法如遗传算法、模拟退火和粒子群优化等，则更适合处理非连续、非线性的优化问题。

### 3.1.2 选择合适的优化技术

选择优化算法时需考虑数据的特性。例如，如果数据集规模很大，梯度下降的变体如随机梯度下降（SGD）会是较好的选择，因为它能够在较短的时间内收敛。当模型出现过拟合时，使用正则化技术如L1或L2惩罚项可以提高模型的泛化能力。

#### *.*.*.* 代码示例与逻辑分析

假设我们要优化一个线性回归模型的损失函数，使用梯度下降算法。下面是一个简单的R语言代码示例：

# 定义线性回归模型的损失函数
loss_function <- function(params, X, y) {
  predictions <- X %*% params
  residuals <- y - predictions
  return(sum(residuals^2))
}

# 梯度下降算法
gradient_descent <- function(X, y, learning_rate, iterations) {
  m <- ncol(X)  # 参数数量
  params <- rep(0, m)  # 初始化参数
  for (i in 1:iterations) {
    predictions <- X %*% params
    residuals <- y - predictions
    gradient <- -t(X) %*% residuals / nrow(X)
    params <- params - learning_rate * gradient
  }
  return(params)
}

# 准备数据
X <- ... # 特征矩阵
y <- ... # 目标向量

# 应用梯度下降算法
final_params <- gradient_descent(X, y, 0.01, 1000)

在上述代码中，`loss_function` 函数用于计算给定参数下的损失，而 `gradient_descent` 函数实现了梯度下降算法。`learning_rate` 参数控制学习的速度，`iterations` 决定了算法迭代的次数。每一步迭代中，参数向量 `params` 会根据损失函数的梯度进行更新，以最小化损失。

### *.*.*.* 参数说明

在 `gradient_descent` 函数中，`learning_rate` 和 `iterations` 是两个关键参数。`learning_rate` 需要仔细选择，太大会导致算法无法收敛，太小则会使收敛过程非常缓慢。`iterations` 应该足够多，以确保算法有足够的时间找到最优解，但过多的迭代会浪费计算资源。

## 3.2 模型调参与验证

在构建了plm模型并选择适当的优化算法后，我们需要对模型进行调参和验证，以确保模型的稳定性和预测准确性。

### 3.2.1 调参策略与实验设计

模型调参是性能优化的重要环节。调参可以手动进行，也可以使用自动化的超参数优化工具，如网格搜索（Grid Search）、随机搜索（Random Search）或贝叶斯优化等。

#### *.*.*.* 代码示例与逻辑分析

假设我们使用网格搜索来寻找最优的超参数组合。以下是R语言中使用`caret`包进行网格搜索的示例：

library(caret)

# 定义训练控制
train_control <- trainControl(method = "cv", number = 10)  # 10折交叉验证

# 使用网格搜索进行调参
grid_search <- train(
  formula = ... ,  # 模型公式
  data = ... ,     # 数据集
  method = "lm",   # 使用线性模型
  trControl = train_control,
  tuneGrid = expand.grid(...)  # 指定要搜索的超参数网格
)

# 输出最佳参数组合
print(grid_search$bestTune)

在这个例子中，我们首先定义了训练控制参数，包括交叉验证的方法和数量。`train`函数执行网格搜索，搜索的范围由`tuneGrid`参数指定。函数的输出是最佳的参数组合，这些参数会给我们带来最优的模型性能。

### 3.2.2 交叉验证与模型稳定性评估

交叉验证是一种评估模型稳定性和泛化能力的技术。它通过将数据集分成多个子集，轮流将其中一个子集作为测试集，其余作为训练集，来评估模型的性能。

#### *.*.*.* 代码示例与逻辑分析

以下是使用k折交叉验证来评估模型稳定性的R语言代码示例：

# 使用 caret 包进行交叉验证
set.seed(123)  # 设置随机种子以保证结果可重复
cv_results <- train(
  formula = ... ,  # 模型公式
  data = ... ,     # 数据集
  method = "lm",   # 使用线性模型
  trControl = trainControl(method = "cv", number = 10)  # 10折交叉验证
)

# 输出交叉验证结果
print(cv_results)

在这个例子中，我们使用了10折交叉验证，每次迭代将10%的数据作为测试集，并使用剩余的90%数据训练模型。通过观察不同迭代中的测试误差，我们可以评估模型的稳定性和泛化能力。

### *.*.*.* 表格展示

为了更好地展示交叉验证的结果，可以创建一个表格来总结测试误差：

| 迭代 | 训练误差 | 测试误差 |
|------|----------|----------|
| 1 | 0.123 | 0.120 |
| 2 | 0.110 | 0.115 |
| ... | ... | ... |
| 10 | 0.125 | 0.121 |

通过比较不同迭代的训练误差和测试误差，我们可以得到关于模型稳定性的直观理解。如果测试误差显著高于训练误差，那么模型可能出现了过拟合。

### *.*.*.* 流程图表示

使用mermaid流程图，我们可以形象地表示交叉验证的过程：

graph TD
    A[开始交叉验证] --> B[划分数据集为训练集和测试集]
    B --> C[用训练集训练模型]
    C --> D[用测试集评估模型]
    D --> E[记录测试误差]
    E --> F{所有折数完成?}
    F --> |是| G[汇总交叉验证结果]
    F --> |否| B
    G --> H[结束交叉验证]

本节通过一系列的代码块、表格和流程图展示了如何选择优化算法、进行模型调参以及应用交叉验证技术来优化plm模型的性能。这些技术的选择和应用将直接影响模型在实际应用中的效果和准确性。随着数据分析方法和计算能力的不断进步，优化技术也在不断进化，模型性能的提升成为了数据分析领域的关键挑战之一。

# 4. plm模型实战应用案例

在深入研究了plm模型的理论与优化方法后，现在让我们着眼于真实世界的案例分析，以展示plm模型如何在不同的领域和数据集中发挥作用。我们将探讨两个不同的案例，首先是针对经济数据分析的应用，随后我们将转向社会科学研究中的应用。通过这些案例，您可以了解如何在实践中运用plm模型解决具体问题，并了解其在实际中的应用价值。

### 4.1 经济数据分析案例

#### 4.1.1 案例背景与数据预处理

经济数据通常包含时间序列和横截面的双重结构，这使得面板数据成为经济分析的重要组成部分。在本案例中，我们考虑一个经济问题：如何评估某一国家不同行业对于国内生产总值（GDP）增长的贡献。

为了回答这个问题，我们收集了过去十年间该国家内多个行业的年度数据，包括行业产出、资本存量、劳动力投入以及一些其他控制变量。数据的预处理步骤包括检查缺失值、异常值处理、数据归一化或标准化以及验证变量间的多重共线性。

在R中，我们可以使用以下代码来进行基本的数据预处理：

# 加载所需的库
library(plm)
library(dplyr)

# 读取数据
data <- read.csv("economic_data.csv", header = TRUE, sep = ",")
head(data)

# 数据清洗：处理缺失值
data <- na.omit(data) # 去除含有NA的行

# 标准化处理
data$capital <- scale(data$capital)
data$labor <- scale(data$labor)

# 检查多重共线性
cor_matrix <- cor(data[, c("output", "capital", "labor")])
print(cor_matrix)

通过这段代码，我们不仅加载了数据，还对数据进行了清理和预处理。特别是，我们标准化了资本和劳动力数据，并且检查了变量间的相关性，以确保模型不会因为共线性问题而产生误导性结果。

#### 4.1.2 plm模型构建与结果解读

在数据预处理之后，我们开始构建plm模型。考虑到数据的时间序列和横截面特性，我们采用适合面板数据的固定效应模型。

# 构建固定效应模型
fixed_effect_model <- plm(output ~ capital + labor, data = data, index = c("industry", "year"), model = "within")
summary(fixed_effect_model)

这里我们定义了模型公式，并指定了面板数据的分组变量。`model = "within"`参数指明了我们使用的是固定效应模型。

在模型构建之后，我们可以解读回归结果来分析资本和劳动力对行业产出的影响。根据模型输出，我们可以查看系数的大小、方向和显著性水平，以及诸如R平方等统计指标。这些解读有助于我们理解在控制个体和时间效应后，资本和劳动力对产出的独立影响。

### 4.2 社会科学研究案例

#### 4.2.1 研究问题与数据特点

在社会科学领域，面板数据模型同样被广泛应用，例如在教育研究中评估不同学校对学生成绩的影响。在此案例中，我们关注的问题是，学校和家庭因素如何共同作用于学生的考试成绩。

我们收集了某个地区连续五年内多个学校学生的学习成绩数据，包括学生的年龄、性别、家庭社会经济状态（SES）以及学校的特征等变量。

在此背景下，plm模型可以帮助我们理解固定于学校和年份的效应，从而准确估计其他协变量对学生成绩的影响。面板数据模型能够控制那些不随时间变化的学校特征（例如地理位置）和学生个人特征，这在普通的截面数据分析中很难实现。

#### 4.2.2 plm模型在社会科学中的应用

构建plm模型的基本思路与经济数据分析案例类似，但是针对社会科学问题，我们可能更关注于模型在解释变量上的解释力和政策含义。

# 构建面板数据模型
school_effect_model <- plm(score ~ age + gender + ses + school_characteristics,
                           data = education_data,
                           index = c("school", "year"),
                           model = "within")
summary(school_effect_model)

在上述代码中，我们使用了plm函数来构建一个固定效应模型。通过模型的输出结果，我们可以评估不同因素（如年龄、性别、家庭SES等）对学生考试成绩的具体影响，并分析其统计显著性。

在应用plm模型于社会科学问题时，我们不仅要关注模型的统计特性，还需要考虑如何从模型结果中获得对于社会现象的深入理解。模型参数的解释不仅要基于统计数据，还要结合相关领域知识进行深入分析。

通过以上案例，我们可以看到plm模型如何在不同领域发挥作用，解决实际问题，并进一步引导我们如何将模型应用扩展到新的领域和不同的数据集。这些实战案例展示了plm模型的强大功能，以及在数据科学实践中价值的重要性。

# 5. plm模型高级应用与展望

## 5.1 面板数据的高级分析技巧

### 5.1.1 面板数据的拓展应用

面板数据（Panel Data）提供了一个独特的数据结构，它结合了横截面（cross-sectional）和时间序列（time-series）数据的特点。这使得面板数据在分析个体随时间的变化以及不同个体之间的差异上具有独特的优势。在应用plm模型时，拓展面板数据的分析技巧能够帮助我们更深入地理解数据，并提取出更加丰富的信息。

例如，面板数据可以让我们估计个体的固定效应，控制不随时间变化的个体异质性。此外，面板数据还允许我们考察变量之间可能存在的动态关系，例如通过构建动态面板数据模型（Dynamic Panel Data Models），研究变量的滞后效应。

在R语言中，通过使用`plm`包，我们可以轻松构建动态面板数据模型：

library(plm)

# 假设数据集为面板数据，有时间序列和个体标识
# 使用pdynmc函数构建动态面板数据模型
pdyn_model <- pdynmc(formula, data, index = c("个体标识", "时间标识"), effect = "twoways")
summary(pdyn_model)

### 5.1.2 多维面板数据模型

随着研究的深入，面板数据模型的复杂性也在增加。多维面板数据模型考虑了除了时间和个体之外的第三个维度，比如空间维度。这使得模型能够捕捉数据在空间上的相关性和异质性，更适用于诸如区域经济、城市规划等领域的研究。

构建多维面板数据模型时，通常需要处理复杂的结构问题，比如嵌套效应、空间滞后项等。在R语言中，可以结合`plm`和`spatialreg`等包来实现：

library(spatialreg)

# 假设data为包含空间标识的面板数据集
# 构建空间滞后面板数据模型（Spatial Lag Model, SLM）
slm_model <- lagsarlm(formula, data, listw, ...)

summary(slm_model)

## 5.2 未来发展方向与挑战

### 5.2.1 R语言在数据分析领域的趋势

R语言作为统计分析和数据科学领域的主导语言之一，它的未来发展方向始终围绕着提高计算效率、扩展新的统计方法、以及更便捷的数据处理能力。随着`plm`和其他相关包的不断更新，R语言在面板数据分析领域的应用将变得更加广泛和深入。

例如，R语言中集成的并行计算（parallel computation）功能可以显著提高数据分析的效率，特别是在处理大规模面板数据集时。而R语言的模块化设计允许研究者和开发者不断添加新的功能和算法，保持了R语言的活力和前沿性。

### 5.2.2 面临的挑战及应对策略

尽管R语言在数据分析方面具有显著优势，但其在处理极大规模数据时仍然面临性能挑战。此外，数据分析的专业性要求越来越高，对R语言使用者的要求也随之增加。

为应对这些挑战，R社区正在积极开发更高效的算法和并行处理技术。同时，也在推广数据分析教育，例如提供免费的在线课程、教程和认证，以培养更多专业的数据分析人才。此外，随着大数据技术的发展，R语言与Hadoop、Spark等大数据平台的集成也在不断加强，提供了强大的数据处理能力。

graph LR
    A[开始面板数据高级分析]
    A --> B[掌握plm模型]
    A --> C[学习使用R语言新工具]
    B --> D[固定效应与动态面板模型]
    B --> E[处理多维面板数据]
    C --> F[并行计算技术]
    C --> G[大数据平台集成]
    D --> H[案例实践]
    E --> H
    F --> I[性能优化]
    G --> I
    H --> J[总结与展望]
    I --> J
    J --> K[结束]

在这一过程中，R语言社区将继续扮演重要角色，通过提供支持、分享经验和技术更新，推动面板数据分析的发展。同时，面对数据科学领域的新要求，R语言也将不断进化，为数据分析专家提供更加高效和专业的工具。