F1-Score：平衡精确率与召回率的艺术与科学

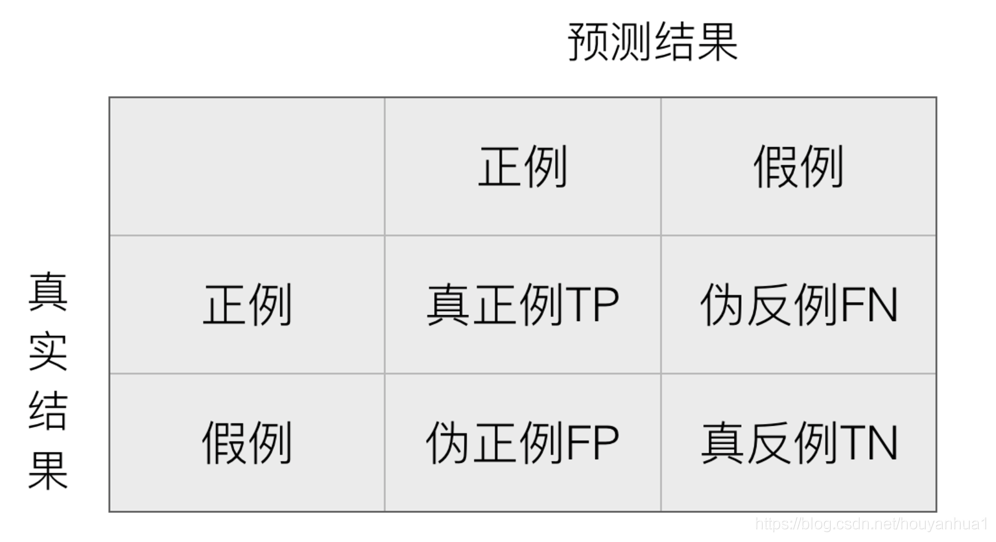
# 1. F1-Score的定义与重要性

在衡量分类模型性能时，准确性（Accuracy）通常不是最佳选择，尤其是在数据不平衡的场景下。**F1-Score**提供了一种全面评价模型性能的方法，是精确率（Precision）和召回率（Recall）的调和平均数。它在二分类问题中特别重要，因为它可以同时考虑预测的准确性和覆盖的完整性。

精确率衡量了预测为正的样本中实际为正的比例，召回率则衡量了实际为正的样本中被正确预测的比例。由于二者往往呈反比关系，F1-Score的引入帮助我们找到一个平衡点，使得这两个指标达到最佳的折中。

在实践中，F1-Score常用于评估信息检索和统计分类任务，尤其是在模型的性能评价需要全面而均衡的视角时。接下来，我们将深入探讨精确率和召回率的理论基础，并进一步解析F1-Score的数学原理及实际应用。

# 2. 精确率和召回率的理论基础

精确率和召回率是评估分类模型性能的两个基本度量，它们在机器学习、数据挖掘以及信息检索等众多领域中扮演着核心角色。了解这些指标的定义和它们之间的关系对于构建有效模型至关重要。

## 2.1 精确率和召回率的概念

### 2.1.1 精确率的定义及其计算方法

精确率（Precision）是指在模型判断为正例（Positive）的样本中，真正为正例的比例。它衡量了模型对正类预测的准确性。精确率的计算方法为：

精确率 = (真正例数) / (真正例数 + 假正例数)

这里的“真正例”指的是正确预测为正类的样本数，而“假正例”指的是错误预测为正类的样本数。在二分类问题中，如果我们将正类标记为1，那么精确率的公式可以用以下Python代码块来表示：

# 假设tp代表真正例的数量，fp代表假正例的数量
def precision(tp, fp):
    return tp / (tp + fp)

### 2.1.2 召回率的定义及其计算方法

召回率（Recall），也称为“真正例率”或“灵敏度”（Sensitivity），是指在所有实际为正例的样本中，模型正确预测为正例的比例。召回率的计算方法为：

召回率 = (真正例数) / (真正例数 + 假负例数)

其中，“假负例”指的是实际为正例却被模型错误预测为负类的样本数。同样假设我们用1表示正类，则召回率的计算可以用以下Python代码块来表示：

# 假设tp代表真正例的数量，fn代表假负例的数量
def recall(tp, fn):
    return tp / (tp + fn)

## 2.2 精确率与召回率的关系与权衡

### 2.2.1 精确率和召回率之间的权衡问题

精确率和召回率之间存在一种天然的权衡关系。当我们提高模型的精确率时（例如，通过增加阈值来判定正类），往往会导致一些本来是正类的样本被排除在外，从而降低了召回率。相反，如果我们增加召回率（例如，降低阈值），则可能会有更多的样本被错误地划分为正类，导致精确率的下降。

在实际应用中，这种权衡需要根据具体的业务场景来做出决策。例如，在垃圾邮件过滤中，我们可能更倾向于高召回率，以确保不漏掉任何一封真正的垃圾邮件。而在线广告点击率预测中，则可能更关注高精确率，以避免浪费广告预算在低效的点击上。

### 2.2.2 为何需要平衡二者

在大多数情况下，我们希望模型能够同时具有较高的精确率和召回率。但是，由于精确率和召回率之间存在权衡，单一地追求任何一个指标都可能导致另一个指标的下降，因此需要在两者之间找到一个平衡点。这个平衡点取决于具体任务的需求和上下文。

为了平衡精确率和召回率，可以采用不同的方法。一种常见做法是使用F1-Score，它是精确率和召回率的调和平均数，可以在两者之间取得平衡。我们将在下一章深入探讨F1-Score的数学原理和实际应用。

在处理精确率和召回率之间的权衡问题时，我们可以绘制精确率-召回率曲线（PR曲线）来可视化不同阈值下的性能变化。PR曲线上的每一点都代表了在特定阈值下模型的精确率和召回率。理想的模型将拥有靠近左上角的PR曲线，这意味着在各个阈值下都能保持较高的精确率和召回率。

graph TD;
    A[Precision] -->|↑| B[Favoring Precision];
    A -->|↓| C[Favoring Recall];
    D[Recall] -->|↑| C;
    D -->|↓| B;
    B -->|↑| E[Threshold];
    C -->|↓| E;
    E --> F[PR Curve];

在上述mermaid流程图中，我们可以看到提高精确率通常会牺牲一些召回率，反之亦然。决策者需要根据实际业务需求来确定在PR曲线上的平衡点。

接下来的章节我们将深入讨论如何将这些理论应用于机器学习模型的评估中，并探讨在实际问题中如何处理F1-Score遇到的挑战。

# 3. F1-Score的数学原理与实现

## 3.1 F1-Score的数学公式解析

### 3.1.1 F1-Score的定义与公式

F1-Score是一类被广泛使用于二分类问题的性能评估指标。它结合了精确率（Precision）和召回率（Recall），是一个单一的指标，用于衡量模型的性能。F1-Score是一个调和平均数，其定义如下：

\[ F1\text{-}Score = 2 \times \frac{Precision \times Recall}{Precision + Recall} \]

该公式将精确率和召回率置于同等重要的位置，并且只有当两者都高时，F1-Score才会高，这使得它成为衡量模型综合性能的有效工具。

### 3.1.2 F1-Score与精确率和召回率的关系

F1-Score通过精确率和召回率的调和平均数，提供了对模型平衡这两个指标性能的能力的评价。在现实世界问题中，很多时候，精确率和召回率难以同时达到高值。因此，F1-Score成为了一个更加全面的衡量标准，使得模型设计者能够在保持较高精确率的同时，也关注召回率的表现，反之亦然。

## 3.2 F1-Score的计算方法

### 3.2.1 F1-Score的标准计算过程

标准的F1-Score计算过程包括以下步骤：

1. 计算精确率和召回率。
2. 将这两个值代入F1-Score的公式。

假设一个二分类问题中，模型对100个样本进行分类，其中真实正类的样本有70个，模型预测出的正类样本有60个，实际预测正确的正类样本有50个。

**精确率（Precision）**计算如下：

\[ Precision = \frac{真阳性}{真阳性 + 假阳性} = \frac{50}{50 + 10} = \frac{50}{60} \]

**召回率（Recall）**计算如下：

\[ Recall = \frac{真阳性}{真阳性 + 假阴性} = \frac{50}{50 + 20} = \frac{50}{70} \]

然后根据F1-Score的公式计算：

\[ F1\text{-}Score = 2 \times \frac{\frac{50}{60} \times \frac{50}{70}}{\frac{50}{60} + \frac{50}{70}} \approx 0.5882 \]

### 3.2.2 F1-Score在不同领域的计算变种

在实际应用中，F1-Score根据不同的领域和需求，可能有变种形式。例如，在多标签分类问题中，F1-Score可以计算为每个类别的平均值，并且可以采取微观或宏观平均的方式。微观平均关注每个类别的性能，而宏观平均则对所有类别的性能计算一个整体的F1-Score。在多任务学习中，一个模型可能同时执行多个任务，每个任务都有自己的F1-Score，需要考虑对这些任务进行加权或平均。

## 代码块示例

以下是使用Python中Scikit-learn库计算F1-Score的代码示例。

from sklearn.metrics import f1_score
import numpy as np

# 示例数据
y_true = np.array([1, 1, 0, 1, 0, 1, 1, 0, 0, 1])
y_pred = np.array([1, 0, 0, 1, 0, 1, 0, 0, 1, 1])

# 计算F1-Score
f1