【链表重排调试技巧】：定位问题的黄金法则

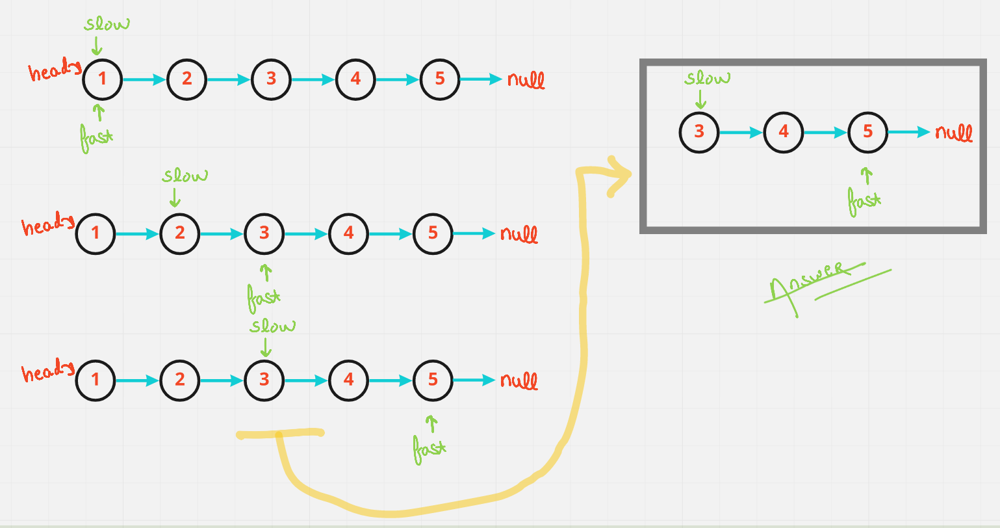
# 1. 链表数据结构概述与重排问题分析

在计算机科学中，链表是一种基础且灵活的数据结构，它由一系列节点构成，每个节点包含数据和指向下一个节点的指针。链表由于其动态内存分配的特性，在插入和删除操作上较数组有优势，但也带来了额外的内存开销和访问延迟。重排问题通常指的是对链表进行排序或调整，以满足特定的顺序需求。

在理解链表重排问题之前，我们首先要熟悉链表的数据结构及其特点。单向链表、双向链表和循环链表是链表的三种主要类型，它们各有不同的应用场合。重排问题的算法逻辑是基于特定排序算法，如冒泡排序、快速排序等，在链表中进行实现。这些排序算法针对链表结构的特点，需要重新设计以适应其非连续存储和指针跳转的特性。

理解链表数据结构和重排算法的原理，对于进行有效调试和性能优化至关重要。在后续章节中，我们将探讨链表重排的理论基础、实践技巧、高级调试技巧以及其在实际项目中的应用。通过对这些内容的学习，读者将能够更加深入地掌握链表重排的方方面面，并在实际开发中有效应用这些技巧。

# 2. 链表重排的理论基础

### 2.1 链表结构的类型与特点

#### 2.1.1 单向链表、双向链表和循环链表的比较

链表是一种常见的数据结构，它由一系列节点组成，每个节点包含数据和指向下一个节点的指针。根据节点间指针方向的不同，链表可以分为单向链表、双向链表和循环链表。

- **单向链表**：节点仅包含指向下一个节点的指针。这种链表结构简单，添加和删除节点时只需要调整指针方向即可，但在需要访问前驱节点时就不适用。

graph LR
  A[开始节点] --> B
  B --> C
  C --> D
  D --> E[结束节点]

- **双向链表**：节点除了有指向下个节点的指针外，还有指向前一个节点的指针。这种结构便于双向遍历，但需要维护更多的指针，增加了复杂性。

graph LR
  A[开始节点] -->|前驱| B
  B -->|前驱| C
  C -->|前驱| D
  D -->|前驱| E[结束节点]
  E -->|后继| D
  D -->|后继| C
  C -->|后继| B
  B -->|后继| A

- **循环链表**：链表的尾部节点的指针指向头部节点，形成一个环。在循环链表中，任何节点都可以被当作链表的起点。

graph LR
  A[头部节点] --> B
  B --> C
  C --> D
  D --> E[尾部节点]
  E --> A

在实际应用中，选择合适的链表类型对性能和资源管理有着重要影响。例如，双向链表适合于需要频繁进行插入和删除操作的场景，而循环链表适合于需要从任一点开始遍历的场景。

#### 2.1.2 链表节点的存储与引用机制

链表节点的存储和引用机制是其核心部分。在大多数编程语言中，节点通常由结构体或类来实现，包含数据字段和引用字段。例如，在C++中，节点定义如下：

struct ListNode {
    int value;
    ListNode* next;
    ListNode(int val) : value(val), next(nullptr) {}
};

在引用机制上，每个节点通过其next指针指向下一个节点，构成一条链。对于双向链表，每个节点还需要保存一个指向previous节点的指针。如果指针管理不当，就可能导致内存泄漏或者悬挂指针（野指针）问题。

### 2.2 链表重排的算法逻辑

#### 2.2.1 算法原理和步骤

链表重排通常指的是对链表节点进行重新排列，以达到特定的顺序要求，常见于排序算法中。其基本原理是对链表中的节点进行比较和交换位置，直到满足既定的排序规则。重排步骤如下：

1. 选择一个排序算法（例如冒泡排序、快速排序等）。
2. 对链表节点进行比较和交换操作。
3. 重复操作直至链表完全排序。

#### 2.2.2 重排中的时间复杂度与空间复杂度分析

链表重排算法的时间复杂度和空间复杂度与所选排序算法紧密相关：

- **时间复杂度**：对于冒泡排序、选择排序这类比较简单的算法，时间复杂度通常是O(n^2)，其中n是链表中节点的数量。快速排序和归并排序的时间复杂度为O(n log n)，但快速排序的最坏情况时间复杂度为O(n^2)。
- **空间复杂度**：链表重排算法的空间复杂度主要取决于排序过程中额外的存储需求。例如，归并排序在链表版本中需要O(n)的额外空间，而快速排序需要根据实现方式决定，理论上是O(log n)，但在最坏情况下可能退化到O(n)。

### 2.3 常见链表重排算法的对比

#### 2.3.1 冒泡排序、选择排序与插入排序在链表中的应用

- **冒泡排序**：通过重复遍历链表，比较相邻节点并将较大的节点“冒泡”到链表的后端。其适用于链表排序，但效率较低，不适用于大数据量排序。
- **选择排序**：重复选择未排序部分的最小（或最大）节点，并将其放置到已排序序列的尾部。选择排序不需要额外存储空间，但时间复杂度较高。
- **插入排序**：构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。对于链表来说，插入操作通常较为高效。

#### 2.3.2 快速排序与归并排序的链表版本

- **快速排序**：选择一个基准元素，将链表分为两部分，使一部分中的所有元素都不大于基准值，另一部分中的所有元素都不小于基准值，然后递归地对这两部分继续进行快速排序。快速排序的链表实现比数组版本效率低，因为它不能通过索引直接访问节点，但可以通过使用尾指针提高效率。
- **归并排序**：将链表分为若干子链表，对每个子链表进行排序，最后将有序的子链表合并为最终的排序链表。归并排序在链表排序中效率较高，尤其是对于链表这种随机访问性能较差的数据结构。

### 代码示例

class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None

def merge_sort(head):
    if not head or not head.next:
        return head

    # Split the linked list into halves
    middle = get_middle(head)
    next_to_middle = middle.next
    middle.next = None
    left = merge_sort(head)
    right = merge_sort(next_to_middle)

    sorted_list = sorted_merge(left, right)
    return sorted_list