【链表重排案例深度解析】：理解问题本质的思维路径

# 1. 链表重排问题概述

在计算机科学中，链表是一种基础且广泛使用于各种数据结构中的线性数据结构。不同于数组的连续内存分配，链表的节点由两部分组成：存储数据的主体以及指向下一个节点的引用（指针）。链表结构在实现上具有灵活性，但在数据访问速度上往往不如数组高效。

链表重排问题是在给定一系列链表节点的情况下，通过重新链接这些节点，达到某种特定的排序或顺序要求。这个过程可能涉及到对链表节点的插入、删除以及节点的重新定位等操作。重排问题在数据处理和计算机科学的其他领域中是非常常见的，尤其是在链表操作频繁的场景中，如内存管理、缓存置换算法等。

在接下来的章节中，我们将深入探讨链表重排的理论基础、实践案例分析以及高级技巧，旨在帮助读者对链表重排问题有一个全面而深刻的理解。无论是初学者还是资深从业者，本章的内容都将为他们解决链表重排问题提供一个坚实的理论基础和实践指导。

# 2. 链表重排的理论基础

## 2.1 链表数据结构介绍
链表是一种基本的线性数据结构，它由一系列节点组成，每个节点包含数据部分和指向下一个节点的指针。链表可以用来实现各种数据结构，例如列表、堆栈、队列、散列表等等。

### 2.1.1 链表的定义和类型

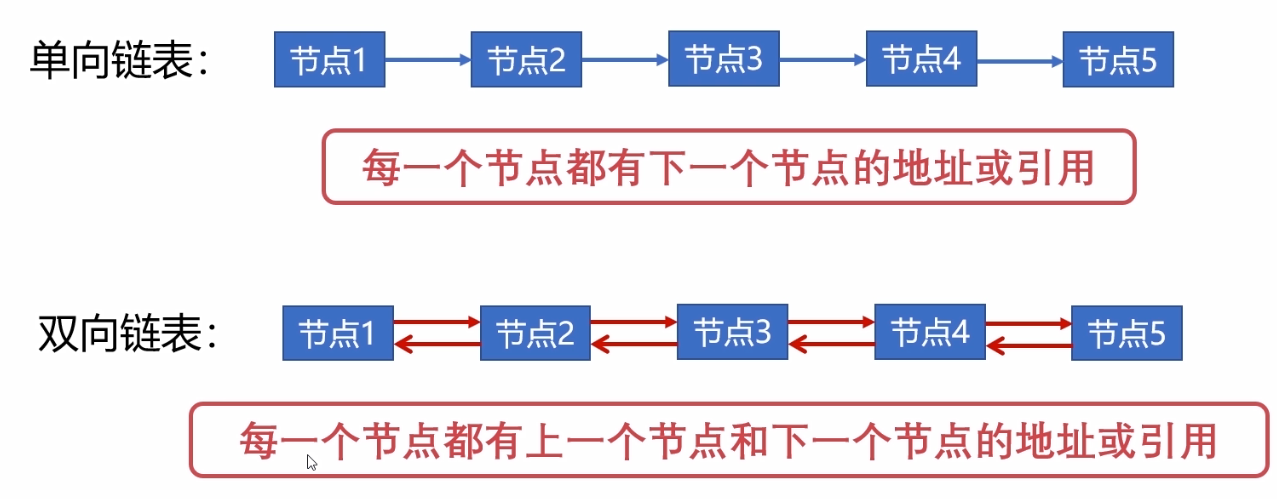
链表可以分为单链表、双链表和循环链表。

- **单链表**：节点只包含一个指针，指向下一个个节点，最后一个节点的指针指向NULL。
- **双链表**：每个节点包含两个指针，一个指向前一个节点，一个指向下一个节点。
- **循环链表**：最后一个节点指针不是指向NULL，而是指回第一个节点，形成一个环。

这些链表类型在实际应用中各有优劣，选择合适的链表类型对于优化数据结构的性能至关重要。

### 2.1.2 链表节点的操作与特性

链表节点的操作包括但不限于创建节点、插入节点、删除节点、查找节点和遍历节点。

- **创建节点**：通常包含数据域和指针域。数据域存储数据，指针域存储指向下一个节点的引用。
- **插入节点**：可以在链表的开头、中间或末尾插入节点。
- **删除节点**：需要调整相关节点的指针，使得删除节点后的链表仍然连贯。
- **查找节点**：从头节点开始，遍历链表查找特定数据的节点。
- **遍历节点**：按顺序访问链表中的每个节点，常用于打印或处理数据。

链表的主要特性是动态大小、非连续存储和高效插入/删除操作。它们不依赖于预先分配的存储空间，而是根据需要动态地分配和释放内存。

## 2.2 重排算法的基本原理

### 2.2.1 时间复杂度与空间复杂度分析

重排算法，或者说链表操作的时间复杂度主要由遍历链表的操作决定。链表的插入和删除操作平均时间复杂度为O(1)，前提是已经定位到了操作位置。而查找操作的时间复杂度为O(n)，因为链表不支持随机访问。

空间复杂度在链表操作中通常是O(1)，因为除了必要的节点数据外，操作过程中一般不需要额外的空间。

### 2.2.2 重排算法的核心思想

重排算法的核心思想是维护链表中节点的相对顺序，使其满足特定的规则或条件。这些规则可以是数值的升序或降序排列，也可以是按照节点地址的排列等。

对于链表重排来说，核心在于掌握链表节点的移动技巧，了解如何在不同节点间进行正确的指针操作，以及如何有效利用现有节点来完成链表的重组。

## 2.3 重排问题的约束条件

### 2.3.1 单链表与双链表的区别

在重排链表时，双链表比单链表有更多的灵活性，因为双链表允许双向遍历。这意味着双链表在重排时可以更容易地交换相邻节点，从而在某些情况下提高重排的效率。

### 2.3.2 循环链表的特殊处理

循环链表的特殊处理在于其闭合的特性，重排循环链表时需要确保最终的状态仍然是一个有效的循环链表，即最后一个节点指向链表的头节点。

这要求在算法中对循环链表的边界条件进行额外的检查，以避免出现无限循环的错误。

# 3. 链表重排实践案例分析

## 3.1 单链表的重排实践

### 3.1.1 重排单链表的基本步骤

单链表的重排是算法问题中常见的一类问题，其核心在于重新安排链表节点的指向，使得原本无序的节点按照一定的顺序排列。对于单链表而言，我们一般会通过调整节点的指针方向来完成重排任务。

在实际操作中，首先需要遍历整个链表，记录下链表的长度，同时将链表拆分为两个子链表，一个包含所有奇数位置的节点，另一个包含所有偶数位置的节点。接下来，通过调整指针的方向，将偶数链表插入到奇数链表之间，实现整个链表的重排。

下面以一个简单的例子来解释这个过程：

1. 首先，我们初始化三个指针：`odd` 指向奇数位置的第一个节点，`even` 指向偶数位置的第一个节点，`evenHead` 指向偶数链表的头部。

2. 然后，遍历原链表，每次移动两个节点，直到遍历结束。

3. 接下来，将 `even` 链表的最后一个节点的 `next` 指针指向 `odd` 链表的下一个节点。

4. 最后，将 `odd` 链表的 `next` 指针指向 `evenHead`，完成重排。

通过以上步骤，我们能够将一个随机排列的单链表重排为一个有序的链表，其中节点按照原始顺序的奇偶位置重新排列。

### 3.1.2 常见问题的解决方法

在实际应用中，可能遇到多种特殊情况，比如空链表、只有一个节点的链表、节点数为偶数的链表等。下面是一些常见问题及其解决方法：

1. **空链表或只有一个节点的链表**：这种情况下，不需要进行任何操作，链表本身就是重排后的结果。

2. **节点数为偶数的链表**：步骤与节点数为奇数的链表相同，不过最终偶数链表的尾部节点将指向 `null`，因为原链表的最后一个节点是奇数位置。

3. **节点值重复情况**：当链表中存在重复值时，重排逻辑不变，但可能需要额外处理重复值的逻辑，比如确保重排后的链表中偶数位置的节点值小于奇数位置的节点值。

为了处理这些问题，代码实现时应该包含相应的判断逻辑，并进行相应的操作。下面是处理节点数为偶数的单链表重排的代码示例：

class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

def reorderList(head):
    if not head or not head.next:
        return head
    # 分割链表
    slow, fast = head, head.next
    while fast and fast.next:
        slow = slow.next
        fast = fast.next.next
    odd = head
    even = slow.next
    slow.next = None
    # 反转偶数部分链表
    prev = None
    while even:
        tmp = even.next
        even.next = prev
        prev = even
        even = tmp
    # 合并两个链表
    even = prev
    while even:
        odd_tmp = odd.next
        even_tmp = even.next
        odd.next = even
        eve