噪声抑制在数字信号处理中的应用：PPT课件教你处理干扰


参考资源链接：[数字信号处理（第三版）PPT课件](https://wenku.csdn.net/doc/645f4789543f8444888b11a3?spm=1055.2635.3001.10343)
# 1. 数字信号处理基础

在现代信息技术领域中，数字信号处理(Digital Signal Processing, DSP)是核心组成部分，它涉及到通过数字计算的方式对信号进行分析、修改、增强以及合成等操作。数字信号处理涉及两个基本类型的数据：离散时间信号和离散值信号。

## 1.1 数字信号的分类

在数字信号处理中，信号通常可以被分类为模拟信号和数字信号。模拟信号是连续的，可以通过时间连续地取值；而数字信号则是由一系列离散的值组成，其处理依赖于数字计算。

### 离散时间信号
离散时间信号是指在特定的时间点上有定义的信号，其值可以连续变化，但只在离散的时间点上取值。这种信号可以由计算机直接处理。

### 离散值信号
离散值信号（数字信号）则是在时间上离散，并且在值上也是离散的。这种信号在实际生活中十分常见，例如电话中的数字音频。

## 1.2 数字信号处理的基本操作

数字信号处理涵盖了各种操作，比如信号变换、滤波、压缩、解压缩等。最基本的操作之一是离散傅里叶变换（Discrete Fourier Transform, DFT），它允许我们在时域和频域之间转换信号，为信号分析和处理提供了一个强大的数学工具。

### 离散傅里叶变换（DFT）
DFT能够将离散时间信号从时域转换到频域。该变换的逆操作是逆离散傅里叶变换（Inverse DFT，IDFT），用于将信号从频域转换回时域。

### 窗函数和滤波器
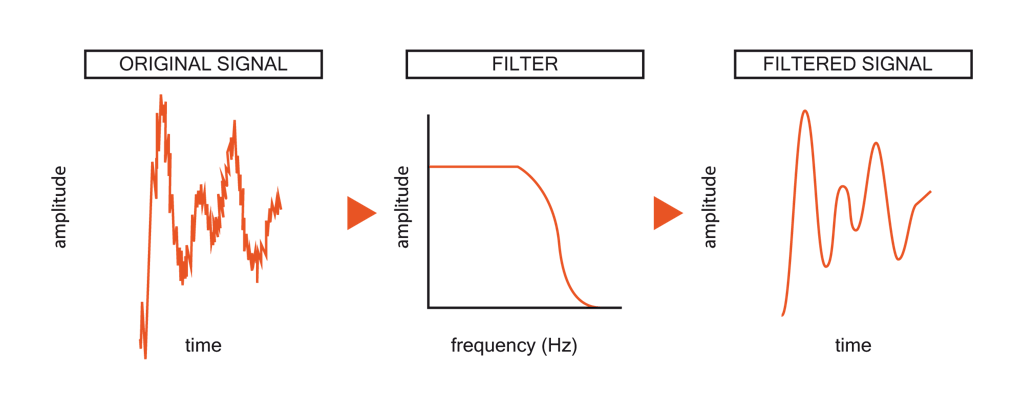
在处理信号时，常常使用窗函数来减少边缘效应。而滤波器则用于从信号中去除不需要的频率成分，仅保留所需成分，这在噪声抑制等应用中至关重要。

通过这些基础操作，数字信号处理可以实现对各种信号的精确控制，从而支持音频处理、图像处理、通信系统等众多技术领域。随着技术的发展，数字信号处理技术变得越来越复杂，对于提高信号质量、降低噪声影响等方面具有不可替代的作用。

# 2. 噪声和干扰的理论分析

噪声和干扰是数字信号处理中不可避免的问题，它们会严重影响信号的质量和通信的效率。为了更有效地抑制噪声和干扰，首先需要对其有一个深入的理解。

### 2.1 噪声的定义和分类

噪声是任何与所需信号不同的、无用的电信号，它在传播路径中无规则地出现，通常会降低信号的可懂度。噪声可以根据不同的特性被分为不同类型。

#### 2.1.1 白噪声、粉红噪声与热噪声

- **白噪声**：频谱分布均匀，功率谱密度在整个频率范围内恒定。它类似于光谱中的白光，因为包含所有频率的等量信号能量。
- **粉红噪声**：其功率谱密度与频率成反比，大约每降低10dB，频率增加10倍。粉红噪声更接近许多自然和人造信号的实际噪声分布。
- **热噪声**：又称约翰逊-奈奎斯特噪声，它是由导体内部电荷载体的随机热运动引起的。其功率与温度和带宽成正比，与电阻值成正比。

# 生成1秒钟的白噪声信号示例
import numpy as np
import matplotlib.pyplot as plt

# 设置采样频率为44.1kHz
fs = 44100
# 生成时间向量
t = np.linspace(0, 1, fs, endpoint=False)
# 生成白噪声数据
white_noise = np.random.normal(0, 1, len(t))

plt.plot(t, white_noise)
plt.title('White Noise')
plt.xlabel('Time [s]')
plt.ylabel('Amplitude')
plt.show()

#### 2.1.2 内部噪声与外部噪声的区别

- **内部噪声**：来自系统内部的噪声，例如设备产生的电子噪声（热噪声）和量子噪声。
- **外部噪声**：源自系统外部的噪声，比如工业干扰、大气噪声以及人为产生的干扰等。

### 2.2 干扰的影响分析

干扰会破坏信号的完整性，对信号产生不良的影响，从而降低通信的质量。

#### 2.2.1 干扰的来源和类型

- **人为干扰**：由人类活动产生的干扰，比如无线通信设备的杂散信号。
- **自然干扰**：自然界中产生的干扰，例如雷电和太阳风暴。
- **系统内部干扰**：系统内部各部分间的相互干扰，可能由电源、电缆等引起。

#### 2.2.2 干扰对信号的影响机制

干扰通常会在信号传输过程中叠加在信号上，改变信号的幅度、相位或频率，从而产生失真。失真的积累可能超过系统容错范围，导致数据错误。

### 2.3 噪声抑制的重要性

噪声抑制对于提升信号质量至关重要，它直接影响到通信系统的性能。

#### 2.3.1 信号质量的评价指标

- **信噪比（SNR）**：表示信号强度与背景噪声强度的比值，是一个衡量信号质量的常用指标。
- **总谐波失真（THD）**：衡量一个系统非线性失真的程度，表示除了基频外，信号中其他谐波的强度和基频强度的比率。

#### 2.3.2 噪声抑制对通信质量的提升

通过有效的噪声抑制，可以提高信号的清晰度，减少误码率，进而提高整个通信系统的数据传输效率和可靠性。噪声抑制不仅提升了通信质量，还可以提高信号处理系统的整体性能，延长设备的使用寿命。

# 3. 噪声抑制技术的原理与方法

## 3.1 滤波技术基础

在数字信号处理中，滤波技术是基本且广泛使用的噪声抑制方法。滤波器可以通过允许特定频率范围的信号通过，同时抑制其他频率的信号，来达到改善信号质量的目的。

### 3.1.1 低通、高通、带通和带阻滤波器

滤波器主要分为四种基本类型：低通、高通、带通和带阻滤波器。

- **低通滤波器**只允许低于某个截止频率的信号成分通过。
- **高通滤波器**允许高于截止频率的信号通过，阻挡低频部分。
- **带通滤波器**允许一个特定频率范围内的信号通过，而阻挡其他频率。
- **带阻滤波器**则阻止一个特定频率范围的信号，允许其他频率通过。

下面是一个简单的低通滤波器的数学模型与实现示例：

import numpy as np
import matplotlib.pyplot as plt

def low_pass_filter(input_signal, cutoff_freq, sampling_rate, order=2):
    # 参数说明：
    # input_signal: 输入信号
    # cutoff_freq: 截止频率
    # sampling_rate: 采样率
    # order: 滤波器阶数
    nyq = 0.5 * sampling_rate  # 计算Nyquist频率
    normal_cutoff = cutoff_freq / nyq
    # 创建低通滤波器
    b, a = butter(order, normal_cutoff, btype='low', analog=False)
    output_signal = lfilter(b, a, input_signal)
    return output_signal

# 示例使用低通滤波器
Fs = 48000  # 采样率
t = np.linspace(0, 1.0, int(Fs))  # 时间向量
a = 0.02
f0 = 1000
note = np.sin(2 * np.pi * f0 * t)
noise = 0.01 * np.random.randn(len(t)) # 高频噪声
noisy_note = note + noise

# 应用低通滤波器
filtered_note = low_pass_filter(noisy_note, cutoff_freq=1500, sampling_rate=Fs)

# 绘制信号
plt.figure(figsize=(12, 8))
plt.subplot(2,1,1)
plt.plot(t, noisy_note)
plt.title('Noisy Note')
plt.subplot(2,1,2)
plt.plot(t, filtered_note)
plt.title('Filtered Note')
plt.tight_layout()
plt.show()

在这个示例中，我们使用了`scipy.signal`库中的`butter`和`lfilter`函数来设计和应用一个低通滤波器。这段代码首先创建了一个噪声信号，然后应用了一个低通滤波器来去除高频噪声。

### 3.1.2 数字滤波器的设计与实现

数字滤波器的设计与实现可以分为以下几个步骤：

1. 确定滤波器的类型和规格，例如，定义通带和阻带的频率范围及纹波大小。
2. 根据这些规格选择适当的滤波器结构，例如FIR或IIR滤波器。
3. 利用软件工具设计滤波器系数，如使用脉冲响应不变法或双线性变换法。
4. 实现滤波器，例如通过直接实现差分方程，或者利用快速傅里叶变换(FFT)技术。

from scipy.signal import butter, lfilter

def butter_lowpass(cutoff, fs, order=5):
    nyq = 0.5 * fs  # Nyquist Frequency
    normal_cutoff = cutoff / nyq
    b, a = butter(order, normal_cutoff, btype='low', analog=False)
    return b, a

# 使用设计好的滤波器
def butter_lowpass