线性表的顺序存储结构与链式存储结构对比分析

# 1. 线性表的顺序存储结构

顺序存储结构是一种将数据元素顺序存放在一块连续的存储空间中的存储方式。线性表的顺序存储结构通过数组来实现，可以随机访问任意位置的元素，使得查找操作十分高效。在顺序存储结构中，元素之间的物理位置是连续的，这样也方便进行元素的插入和删除操作。然而，插入和删除操作可能涉及到元素的移动，导致效率不如查找高。另外，顺序存储结构需要预先分配一定大小的空间，可能存在空间浪费的情况。总的来说，顺序存储结构适用于需要频繁查询元素位置的场景，但对于频繁插入和删除操作较多的情况，可能不那么适用。

# 2. 线性表的链式存储结构

链式存储结构是线性表的另一种存储方式，相比于顺序存储结构，更加灵活。在链式存储结构中，每个元素都存储了下一个元素的地址，通过地址的指向来实现元素之间的连接。

#### 2.1 链式存储结构简介

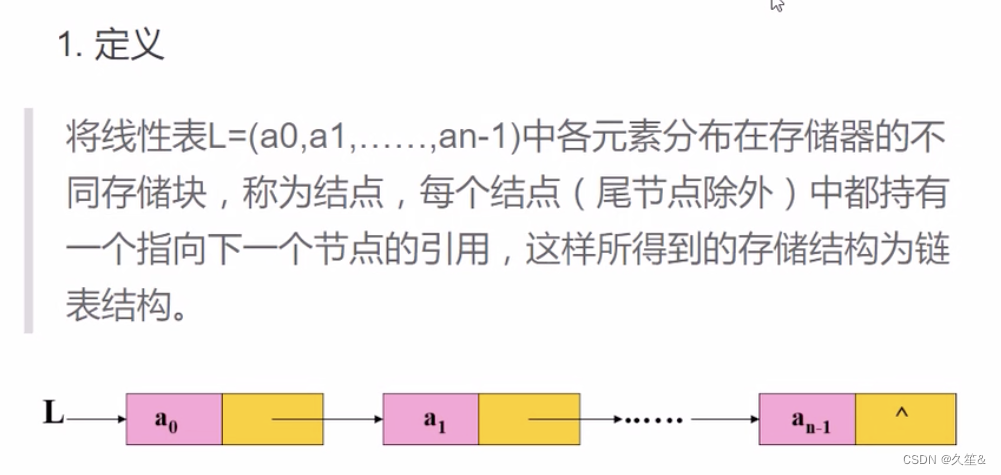
链式存储结构由一系列节点组成，每个节点除了存储数据元素外，还包含指向下一个节点的指针。通过节点之间的指针联系，形成一个链表。链表由头节点开始，依次连接下一个节点，直至末尾节点。链表可以是单向的、双向的，甚至循环的。

链式存储结构相比顺序存储结构的优势在于插入和删除操作更加高效，因为不需要移动大量元素，只需修改指针即可完成。同时，链表的长度可以动态增加，不受固定的存储空间限制。

#### 2.2 链式存储结构的实现方式

链式存储结构可以通过各种语言实现，下面以 Python 语言为例，展示一个简单的单向链表的实现过程。

# 定义链表节点类
class Node:
    def __init__(self, data=None):
        self.data = data
        self.next = None

# 定义链表类
class LinkedList:
    def __init__(self):
        self.head = None

    # 在链表末尾插入节点
    def append(self, data):
        new_node = Node(data)
        if self.head is None:
            self.head = new_node
            return
        last = self.head
        while last.next:
            last = last.next
        last.next = new_node

    # 打印链表元素
    def print_list(self):
        curr = self.head
        while curr:
            print(curr.data)
            curr = curr.next

# 创建链表
llist = LinkedList()
llist.append(1)
llist.append(2)
llist.append(3)

# 打印链表
llist.print_list()

上述代码实现了一个简单的单向链表，通过调用 `append` 方法可以在链表末尾插入新节点，并通过 `print_list` 方法打印链表中的所有元素。

通过链式存储结构，我们能够更加灵活地管理数据，实现各种数据结构和算法，为实际问题提供更多解决方案。

# 3. 顺序存储结构与链式存储结构的区别

#### 3.1 存储方式对比
- 3.1.1 顺序存储结构的存储方式
顺序存储结构使用数组实现，元素在内存中按顺序存储，通过元素在数组中的位置来访问元素，直接存储元素值。

      # 顺序存储结构示例代码
      list_a = [1, 2, 3, 4, 5]
      print(list_a[2])  # 输出结果为 3

- 3.1.2 链式存储结构的存储方式
链式存储结构使用指针将元素串联起来，每个元素存储数据和下一个元素的地址，通过链表的遍历访问元素。

      # 链式存储结构示例代码
      class Node:
          def __init__(self, data=None):
              self.data = data
              self.next = None

      node_a = Node(1)
      node_b = Node(2)
      node_a.next = node_b

#### 3.2 插入与删除操作效率对比
- 3.2.1 顺序存储结构的插入与删除
在顺序存储结构中，插入和删除元素涉及到移动其他元素的位置，时间复杂度为 O(n)。

- 3.2.2 链式存储结构的插入与删除
在链式存储结构中，插入和删除元素只需修改相邻元素的指针，时间复杂度为 O(1)。

#### 3.3 空间利用率对比
- 3.3.1 顺序存储结构的空间利用率
顺序存储结构需要预先分配一定长度的数组空间，可能造成空间浪费或不够用的情况。

- 3.3.2 链式存储结构的空间利用率
链式存储结构可以动态分配内存空间，更加灵活，避免了固定长度造成的空间浪费。

通过以上对比可见，顺序存储结构和链式存储结构在存储方式、操作效率和空间利用率方面各有优劣。深入理解不同存储结构的特点，有助于根据实际需求选择最适合的数据结构。

# 4. 适用场景比较

### 4.1 数据操作类型需求对比

#### 4.1.1 适用于频繁查询的场景
在数据操作中，如果需要频繁进行查询操作，顺序存储结构通常更为高效。由于顺序存储结构的元素在内存中是连续存储的，可以通过计算偏移量来直接访问元素，从而实现快速查询。相比之下，链式存储结构需要通过指针一个个地遍历节点，效率不如顺序存储结构高。

# Python 代码示例：顺序存储结构查询元素
def search_element(arr, target):
    for i in range(len(arr)):
        if arr[i] == target:
            return i
    return -1

# 定义一个顺序存储结构的列表
arr = [1, 2, 3, 4, 5]
target = 3
result = search_element(arr, target)
print(f"元素 {target} 在列表中的索引为：{result}")

#### 4.1.2 适用于频繁插入删除的场景
当数据操作中频繁进行插入和删除操作时，链式存储结构更具优势。在链式存储结构中，插入和删除一个节点只需要改变指针的指向，不需要移动其他元素，因此效率较高。而顺序存储结构在插入和删除操作时，需要移动元素位置，效率较低。

# Python 代码示例：链式存储结构删除节点
class Node:
    def __init__(self, data=None):
        self.data = data
        self.next = None

def delete_node(head, target):
    dummy = Node(0)
    dummy.next = head
    cur = dummy
    while cur.next:
        if cur.next.data == target:
            cur.next = cur.next.next
            break
        cur = cur.next
    return dummy.next

# 创建一个链表并删除指定节点
node1 = Node(1)
node2 = Node(2)
node3 = Node(3)
node1.next = node2
node2.next = node3

new_head = delete_node(node1, 2)

### 4.2 存储规模与效率比较

#### 4.2.1 小规模数据存储对比
对于小规模数据存储，通常情况下顺序存储结构更适合。由于小规模数据存储时，顺序存储结构可以更好地利用内存块、预读取等优势，提高访问效率。而链式存储结构会因为频繁的内存申请和释放，带来额外的开销。

graph LR
    A[顺序存储结构] --> B{小规模数据}
    B --> C[适用]
    A --> D[链式存储结构]
    D -.-> E{小规模数据}
    E -.-> F[不太适用]

#### 4.2.2 大规模数据存储对比
当数据规模较大时，链式存储结构更具优势。由于链式存储结构不需要一块连续的内存空间来存储所有元素，可以根据需要动态分配内存，方便管理大规模数据。相比之下，顺序存储结构需要一段连续的内存空间，当数据量大到超出内存限制时会受到限制。

graph LR
    A[顺序存储结构] --> B{大规模数据}
    B --> C[不太适用]
    A --> D[链式存储结构]
    D --> E{大规模数据}
    E --> F[适用]

#### 4.2.3 内存占用情况的考量
在选择存储结构时，还需考虑数据所占内存空间的情况。顺序存储结构因为需要一整块连续的内存空间来存储所有元素，可能会造成内存浪费。而链式存储结构可以灵活分配内存，更有效地利用内存空间。

综上所述，在具体应用场景中，需根据数据操作类型、存储规模以及内存占用情况等因素综合考虑，选择适合的存储结构来提高效率和性能。

# 5. 代码示例及效率比较

在本章中，我们将通过具体的代码示例来演示顺序存储结构和链式存储结构在插入、删除和空间利用效率方面的差异。同时，我们会对比它们在不同场景下的适用性，以帮助读者更好地理解何时选择使用顺序存储结构或链式存储结构。

#### 5.1 代码示例

##### 5.1.1 顺序存储结构示例

# 初始化一个顺序存储结构的线性表
arr = [1, 2, 3, 4, 5]

# 在第三个位置插入元素6
arr.insert(2, 6)

# 删除第一个元素
arr.pop(0)

print(arr)

##### 5.1.2 链式存储结构示例

class Node:
    def __init__(self, data=None):
        self.data = data
        self.next = None

# 初始化一个链表
head = Node(1)
head.next = Node(2)
head.next.next = Node(3)

# 在第二个节点后插入新节点
new_node = Node(4)
new_node.next = head.next.next
head.next.next = new_node

# 删除第一个节点
head = head.next

while head:
    print(head.data)
    head = head.next

#### 5.2 效率比较

##### 5.2.1 插入与删除操作效率对比

- 顺序存储结构的插入与删除操作的时间复杂度为 O(n)。
- 链式存储结构的插入与删除操作的时间复杂度为 O(1)。

##### 5.2.2 空间利用率对比

- 顺序存储结构的空间利用率受到固定数组长度的限制，可能造成内存浪费。
- 链式存储结构的空间利用率较高，可以动态调整内存空间。

通过以上代码示例和效率比较可以看出，在插入、删除操作频繁且数据规模动态变化的场景下，链式存储结构具有明显的优势。而在数据量较小且对内存占用有严格要求的场景下，顺序存储结构可能更适合。

综上所述，选择合适的存储结构取决于具体需求和场景，开发者需要根据实际情况进行权衡选择。

以上是关于代码示例及效率比较的内容，希望能够帮助读者更好地理解顺序存储结构和链式存储结构的差异和适用性。