BCH码的硬件实现精进:2大设计策略与性能分析
发布时间: 2024-12-15 16:53:10 阅读量: 2 订阅数: 4 


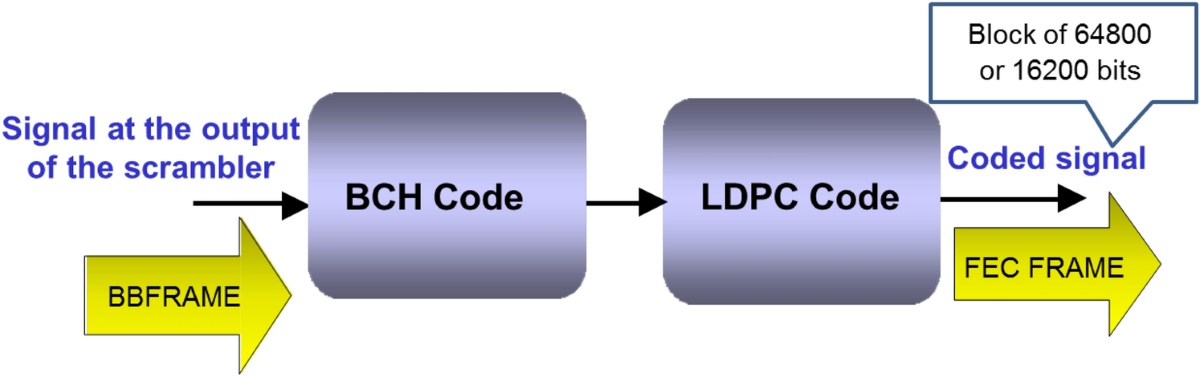
通信与网络中的DVB-S2中BCH译码器的硬件设计
参考资源链接:[BCH码编解码原理详解:线性循环码构造与多项式表示](https://wenku.csdn.net/doc/832aeg621s?spm=1055.2635.3001.10343)
# 1. BCH码的硬件实现概述
BCH码(Bose-Chaudhuri-Hocquenghem codes)是广泛应用于数字通信和存储系统中的一种纠错码。其硬件实现的关键在于高效、可靠的编码和解码过程。在数字硬件设计中,BCH码的实现通常通过专用集成电路(ASIC)或现场可编程门阵列(FPGA)来完成,旨在实现高速纠错和低资源消耗。
本章将概述BCH码硬件实现的流程,介绍其在硬件设计中的作用和挑战。通过对BCH码在硬件层面的需求进行分析,为进一步深入研究BCH码的编码和解码过程奠定基础。这包括硬件设计的基本要求、资源分配、以及设计过程中需要考虑的性能指标。
接下来的章节会详细介绍BCH码的理论基础、硬件设计的关键策略、性能分析与优化方法,以及实际应用案例,最终对BCH码硬件实现的未来趋势进行展望。
# 2. BCH码理论基础与编码原理
## 2.1 BCH码的数学模型
### 2.1.1 纠错码和BCH码的定义
纠错码是一种允许在数据传输或存储过程中检测并纠正错误的编码技术。其核心思想是通过添加冗余信息,使得原始数据在受到一定程度的破坏后,仍能恢复出正确的信息。BCH码(Bose-Chaudhuri-Hocquenghem code)是一类重要的线性纠错码,由R.C. Bose和D.K. Ray-Chaudhuri以及A. Hocquenghem独立提出。
BCH码可以被看作是循环码的一个特例,其设计目标是能够纠正多个错误。BCH码的纠错能力与其长度、最小距离和设计参数有关。在实际应用中,BCH码因其良好的纠错性能和结构特性而广受欢迎。
### 2.1.2 BCH码的关键数学公式与算法
BCH码的核心数学理论涉及到有限域(Galois Field)上的多项式运算。对于一个在GF(2^m)上的BCH码,其生成多项式g(x)可以表达为:
\[ g(x) = LCM(m_1(x), m_2(x), ..., m_{2t-1}(x)) \]
其中,\( LCM \)表示最小公倍数,\( m_i(x) \)是第i个错误位置多项式的最小多项式,并且码的最小距离d满足:
\[ d \geq 2t + 1 \]
这里,t是BCH码能纠正的最大错误个数,m是有限域的阶。
生成多项式g(x)的根是一组特定的错误位置的β的倍数,β是有限域的一个本原元素。求解最小多项式 \( m_i(x) \) 和生成多项式g(x)是BCH编码过程中的关键步骤。
### 2.1.3 BCH码的性能评估与选择
BCH码的性能评估通常包括错误校正能力、最小距离、以及编码效率。选择合适的BCH码需要在纠错能力和资源消耗(如存储空间、处理时间)之间进行权衡。例如,一个(7,4)汉明码是一个简单的BCH码,它可以纠正一个错误,并且其最小距离为3。
## 2.2 BCH码的编码过程
### 2.2.1 系统BCH编码的步骤
系统BCH码的编码过程通常遵循以下步骤:
1. **选择有限域和本原多项式**:确定适合的有限域GF(2^m)以及对应的本原多项式。
2. **构建生成多项式**:根据要纠正的错误个数t,找到对应的错误位置多项式并构建生成多项式g(x)。
3. **编码**:将原始信息多项式u(x)乘以生成多项式g(x),得到码字多项式c(x)。
具体的编码算法可以用伪代码表示:
```pseudo
输入:信息多项式 u(x), 有限域 GF(2^m), 纠错能力参数 t
输出:码字多项式 c(x)
1. 选择 GF(2^m) 上的一个本原多项式 p(x)
2. 构建错误位置多项式集合
3. 构建生成多项式 g(x) 为错误位置多项式的最小公倍数
4. 计算码字多项式 c(x) = u(x) * g(x) mod x^n-1
5. 输出 c(x)
```
### 2.2.2 非系统BCH编码的构造方法
非系统BCH编码指的是编码后的码字中并不直接包含原始信息的部分。非系统BCH码的构造通常遵循以下步骤:
1. **生成多项式**:确定生成多项式g(x),通常是一个设计好的特定多项式。
2. **编码**:将信息向量与生成多项式的系数向量进行组合,产生码字。
非系统BCH码的关键在于生成多项式的构造,这通常涉及对有限域内特定元素的幂次关系的研究和分析。
## 2.3 BCH码的解码策略
### 2.3.1 错误定位多项式的计算
BCH码的解码涉及找到错误位置多项式的根,这些根对应于错误在数据中的位置。错误定位多项式σ(x)是关键步骤之一,通常采用综合除法或Berlekamp-Massey算法求解。
错误定位多项式σ(x)的计算过程:
```pseudo
输入:接收到的码字 r(x), 有限域 GF(2^m), 纠错能力参数 t
输出:错误定位多项式 σ(x)
1. 计算伴随式 S(x)
2. 初始化错误定位多项式 σ(x)
3. 使用Berlekamp-Massey算法迭代求解 σ(x)
4. 输出 σ(x)
```
### 2.3.2 错误值的求解算法
一旦错误位置被确定,下一步是求解具体的错误值。求解错误值通常使用Forney算法:
```pseudo
输入:错误位置多项式 σ(x), 接收到的码字 r(x), 错误位置集合
输出:错误值向量
1. 对于每个错误位置,计算错误值
2. 使用Forney算法对每个错误位置进行求解
3. 输出错误值向量
```
以上过程涉及到复杂的数学运算,但在硬件实现中,这些运算可以通过特定的算法优化,以加速处理速度。
# 3. BCH码硬件设计的关键策略
在第三章中,我们深入探讨了实现BCH码硬件设计的关键策略。这些策略涵盖了从总体架构设计到编码器和解码器的具体实现,再到优化策略的深入分析。本章内容旨在为IT专业人士提供一个全面的视角,以了解BCH码在硬件实现过程中如何通过精确的架构和优化技术来提高性能。
## 3.1 硬件架构设计
### 3.1.1 硬件设计的总体原则
在硬件架构设计阶段,需要考虑的首要因素是设计的总体原则。这包括了硬件的可扩展性、灵活性以及对特定应用场景的适应能力。设计原则应该保证硬件实现能够处理不同长度的数据块,并且能够适应未来技术的发展和应用场景的变化。为了实现这些原则,设计团队需要采用模块化的方法,将硬件设计分解为独立的组件,便于修改和升级。
### 3.1.2 并行处理与流水线技术的应用
在硬件设计中,提升处理速度的一个重要途径是采用并行处理和流水线技术。通过将数据处理任务分配到多个处理单元,可以显著提高处理速度。例如,在BCH编码和解码过程中,可以将数据流分割成更小的块,每个块由不同的处理单元同时处理。而流水线技术则允许设计者在同一个处理单元内按照特定的顺序执行多个任务,每个任务处理一部分数据,从而提高整体的吞吐量。
##
0
0





