语音识别技术演进：从传统到深度学习的革命性转变

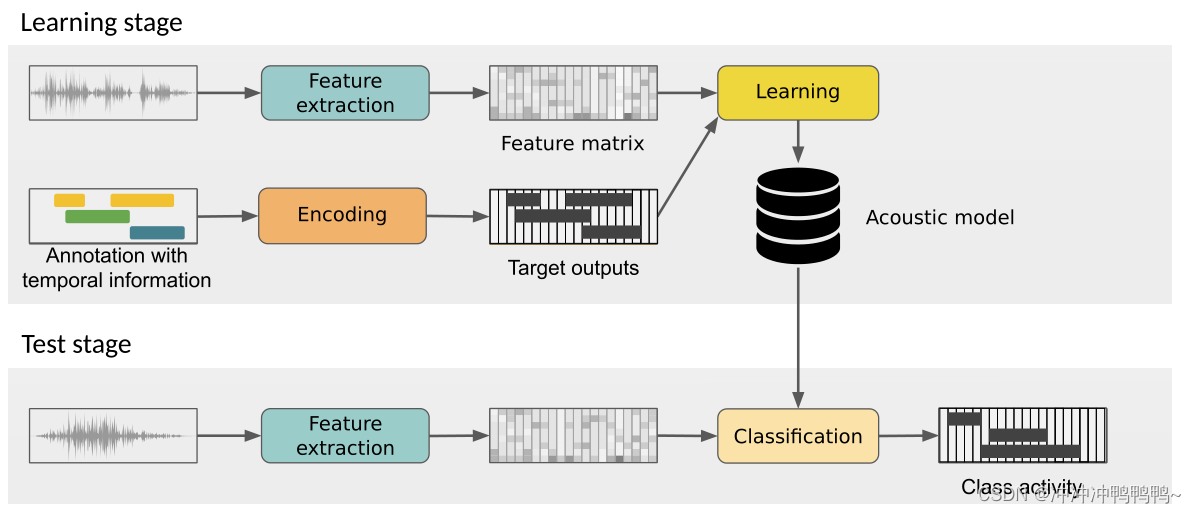
# 1. 语音识别技术的历史演进

语音识别技术，作为人机交互的重要手段，其历史可追溯至20世纪。在这一章中，我们将从其早期的探索开始，介绍语音识别技术从诞生至今的发展历程，以及它在不同阶段所取得的重要进展和里程碑。

## 1.1 早期的语音识别
早在20世纪50年代，科学家们开始尝试构建能够理解人类语音的机器。最初的努力集中在模式匹配技术上，这包括了基于模板的识别方法，它们试图通过预设的语音样本识别语音信号。早期的系统由于技术限制，准确率和应用范围都极为有限。

## 1.2 里程碑式的发展
语音识别技术的一个重要转折点出现在20世纪70年代，当时引入了基于统计的隐马尔可夫模型（HMM）。HMM为语音识别带来了理论基础，显著提升了识别准确性。在此基础上，又进一步发展出了基于神经网络的方法，为后续深度学习技术的应用奠定了基础。

## 1.3 现代语音识别技术的起源
进入21世纪，随着计算能力的提升和大数据技术的发展，语音识别开始进入新的时代。尤其是在2010年后，深度学习的引入彻底改变了语音识别领域，开启了所谓的“现代语音识别时代”。通过深度神经网络和海量数据的训练，系统能以接近人类水平的准确性进行语音识别。

通过本章的探讨，我们可以看到语音识别技术是如何逐步克服挑战，解决局限性，从而达到今天的成就。下一章，我们将深入分析传统语音识别的理论基础和实践应用。

# 2. 传统语音识别的理论基础与实践

## 2.1 语音信号处理

### 2.1.1 信号的预处理和特征提取

语音信号的预处理是将采集到的原始语音信号转换为适用于特征提取的形式的过程。预处理步骤通常包括降噪、去静音段、信号增强等。其目的是减少信号中可能对特征提取产生干扰的无关成分。在预处理后，接下来的特征提取环节至关重要，它直接关系到语音识别的准确性。

特征提取是从预处理后的语音信号中提取有效信息的过程。最常用的特征是梅尔频率倒谱系数（MFCCs）。MFCCs的提取过程主要包括梅尔滤波器组的频率分组、离散傅里叶变换（DFT）以及离散余弦变换（DCT）。

以下是一个MFCC特征提取的Python代码示例，展示了其基本流程：

import numpy as np
from scipy.io import wavfile
from python_speech_features import mfcc

# 读取语音文件
fs, signal = wavfile.read('path_to_audio_file.wav')

# 预处理：确保信号为单声道
if len(signal.shape) > 1:
    signal = signal[:,0]

# 提取MFCC特征
mfcc_features = mfcc(signal, fs)

# 输出MFCC特征
print(mfcc_features)

在上述代码中，首先使用`wavfile.read`函数从WAV文件中读取采样频率（fs）和信号（signal）。然后，确保信号为单声道，因为在大多数语音处理任务中，只使用单个声道的数据。最后，调用`mfcc`函数进行特征提取，并将结果输出到控制台。

### 2.1.2 语音信号的分段与识别单元

语音信号分段通常是按照一定的帧长和帧移来划分语音信号的连续帧。帧长一般设置为20-30ms，而帧移则设置为10ms。每个帧作为独立的单元进行特征提取，这有利于捕捉到语音信号随时间变化的特性。

在确定了语音信号的分段之后，接下来需要定义语音识别的最小单元。在传统的语音识别系统中，这些单元可能是音素、音节或单词。为了识别这些单元，研究人员开发了各种方法，例如动态时间规整（DTW），它通过比较测试语音和模板语音的时间曲线来识别最相似的单元。

## 2.2 语言模型和语音模型

### 2.2.1 统计语言模型的概念与应用

统计语言模型用于描述单词序列出现的概率分布，是语音识别系统不可或缺的一部分。其作用在于提供对某一词序列出现可能性的度量，这对于识别句子的真实度至关重要。基本的统计语言模型包括n元语法（n-gram）模型，它假设一个词的出现只与它前面的n-1个词有关。

n-gram模型可以使用如下公式表示：

P(w_i|w_{i-1}, w_{i-2}, ..., w_{i-n+1}) = P(w_i|w_{i-n+1}^{i-1})

其中，P代表概率，w_i代表句子中的第i个词。

一个简单的Python代码示例来训练一个bigram模型：

from nltk import bigrams
from collections import Counter

# 假设我们有一个包含文本语句的列表
sentences = ["the cat sat on the mat", "the dog sat on the cat"]

# 分词
words = [word.lower() for sentence in sentences for word in sentence.split()]

# 生成bigram
bigram_list = list(bigrams(words))

# 计算bigram出现的频率
bigram_frequency = Counter(bigram_list)

# 计算模型
model = {bg: bigram_frequency[bg] for bg in bigram_frequency}

print(model)

上述代码段首先导入了`bigrams`和`Counter`模块来生成bigram并计算它们的频率。之后，构建一个简单的bigram统计模型。在实际应用中，会根据大量语料库来训练语言模型，并使用更复杂的平滑技术来处理稀疏性问题。

### 2.2.2 语音识别的隐马尔可夫模型（HMM）

隐马尔可夫模型（HMM）是语音识别中用来处理时间序列数据的一个经典模型，它假定系统的行为可以用一个马尔可夫过程来描述。HMM在语音识别中的应用主要体现在将语音信号的每个帧序列对应到一个特定的隐状态序列，这里的隐状态通常对应于声音的某个音素。

HMM模型由三部分组成：状态转移概率、观测概率和初始状态概率。状态转移概率描述了状态之间的转换概率，观测概率描述了某个观测状态在特定隐状态下出现的概率，初始状态概率描述了隐状态序列的起始概率分布。

下面是一个使用Python中`hmmlearn`库的示例，演示了如何构建一个简单的HMM模型：

from hmmlearn import hmm

# 初始化一个HMM模型，以高斯分布为例
model = hmm.GaussianHMM(n_components=3, covariance_type="diag", n_iter=100)

# 假设我们已经有了一些观测数据X和对应的状态数据Y
X = [[0], [0], [1], [1], [2], [2]]
Y = [0, 1, 2, 1, 0, 1]

# 训练模型
model.fit(X, Y)

# 生成状态序列
hidden_states = model.sample(len(X))[1]

print(hidden_states)

在该示例中，首先初始化了一个具有3个状态的高斯分布HMM模型。然后，使用一组观测数据`X`和对应的状态数据`Y`来训练模型。训练完成后，使用`sample`方法来生成状态序列。在实际应用中，观测数据会来自于语音信号特征向量，状态对应于音素或单词。

### 2.2.3 基于规则的识别系统

基于规则的语音识别系统依赖于一系列明确定义的语言学规则和字典。在这样的系统中，语音识别过程被分解为几个步骤：首先将语音信号分解为语音特征；然后根据这些特征来推断最有可能的语音单元；最后，根据语言学知识和字典，组合这些单元形成词和句子。

由于基于规则的系统依赖于详尽的语言规则库和字典，它们往往缺乏灵活性，对噪声和口音的鲁棒性较差。因此，尽管这类系统在理论上可以非常精确，但在实际应用中往往不敌那些利用大量数据进行训练的统计模型，特别是在处理真实世界数据时。

## 2.3 传统技术的局限与挑战

### 2.3.1 处理噪声与变体的难题

噪声是语音识别面临的一个主要挑战之一。现实世界中的环境噪声、远场语音信号的干扰，以及说话人的声音变化等都会对识别的准确性造成影响。传统的语音识别系统在处理这些问题时，通常使用噪声抑制、回声消除和语音增强技术来尽量减少噪声的影响。

一种常用的技术是谱减法，它通过估计噪声功率谱并从带噪信号功率谱中减去估计出的噪声成分，以达到抑制噪声的目的。尽管这些技术在一定程度上能够改善语音识别性能，但在极端噪声条件下，传统系统的识别率仍然难以令人满意。

### 2.3.2 多语种和方言识别问题

全球有成千上万种语言和方言，多语种和方言的识别是语音识别系统面临的另一个巨大挑战。各种语言在音素体系、语法结构和发音习惯上都存在差异，这要求语音识别系统必须能够准确地区分和识别这些差异。

对于多语种语音识别，一个通用的解决办法是构建多语种的语音识别系统，并在系统内部实现多语言切换。在模型训练时，需要收集并标注足够多的多语种数据集。此外，针对特定的方言，还需要收集该方言的大量语料进行训练。然而，由于数据收集和标注的高昂成本，这一任务显得异常艰巨。

接下来的章节将会介绍深