叉积计算秘籍：从几何直观到数学公式

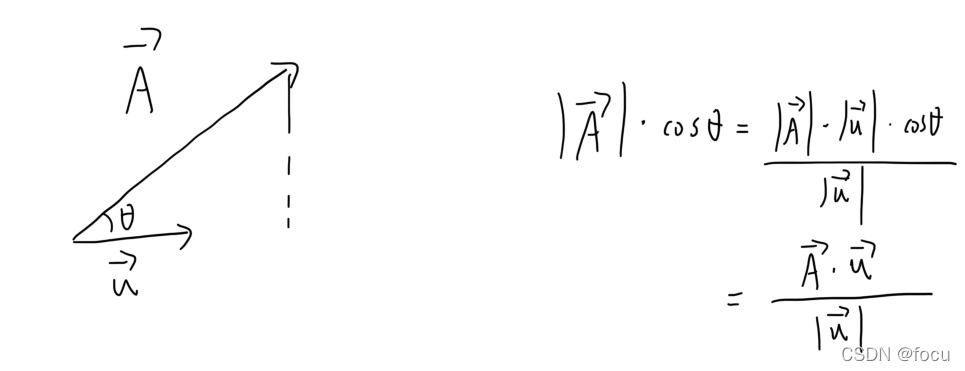
# 1. 叉积的几何直观

叉积是线性代数中一种重要的向量运算，它可以描述两个向量之间的相互作用。几何上，叉积可以用来表示两个向量所张成的平面的法向量，其方向与右手定则一致。

例如，考虑两个向量 **a** 和 **b**，它们的叉积 **a × b** 将产生一个垂直于 **a** 和 **b** 的向量 **n**。向量 **n** 的方向由右手定则决定：将右手的手指沿着 **a** 的方向弯曲，然后将手指沿着 **b** 的方向弯曲，大拇指指向的方向就是 **n** 的方向。

# 2. 叉积的数学公式

### 2.1 叉积的定义和几何意义

叉积，又称向量积，是线性代数中定义在三维欧几里得空间中的二元运算。它将两个三维向量作为输入，并产生一个与这两个向量垂直的第三个三维向量。叉积的几何意义可以直观地理解为两个向量所确定的平行四边形的面积。

### 2.2 叉积的计算公式

#### 2.2.1 行列式法

叉积可以用行列式法计算，具体公式如下：

a × b = | i   j   k |
        | a1  a2  a3 |
        | b1  b2  b3 |

其中，a = (a1, a2, a3) 和 b = (b1, b2, b3) 是两个三维向量，i、j、k 是单位向量。

#### 2.2.2 几何法

叉积也可以用几何法计算。设 a 和 b 是两个三维向量，它们的长度分别为 |a| 和 |b|，夹角为 θ。则叉积的计算公式为：

a × b = |a| |b| sin(θ) n

其中，n 是 a 和 b 所确定的平行四边形的单位法向量。

### 2.3 叉积的性质

叉积具有以下性质：

#### 2.3.1 垂直性和共面性

叉积的结果向量与两个输入向量垂直。如果两个输入向量共线，则它们的叉积为零向量。

#### 2.3.2 方向性和面积性

叉积的方向由右手定则决定。叉积的模长等于两个输入向量所确定的平行四边形的面积。

# 3.1 力矩和转动惯量

叉积在物理学中有着广泛的应用，其中一个重要的应用就是计算力矩和转动惯量。

#### 3.1.1 力矩的计算

力矩是力对物体旋转轴产生的转动效应。其计算公式为：

M = r x F

其中：

- `M` 为力矩，单位为牛米 (N·m)
- `r` 为力作用点到旋转轴的位移向量，单位为米 (m)
- `F` 为作用力，单位为牛顿 (N)

**代码逻辑分析：**

该代码块实现了力矩的计算。`r x F`表示力作用点到旋转轴的位移向量与作用力的叉积。叉积的结果是一个向量，其方向垂直于位移向量和作用力向量，大小等于位移向量和作用力向量构成的平行四边形的面积。

#### 3.1.2 转动惯量的计算

转动惯量是物体对旋转轴的惯性度量。其计算公式为：

I = m * r^2

其中：

- `I` 为转动惯量，单位为千克米平方 (kg·m²)
- `m` 为物体的质量，单位为千克 (kg)
- `r` 为物体质心到旋转轴的距离，单位为米 (m)

**代码逻辑分析：**

该代码块实现了转动惯量的计算。`m * r^2`表示物体的质量乘以质心到旋转轴距离的平方。转动惯量与物体的质量和质心到旋转轴的距离的平方成正比。

# 4. 叉积的进阶应用

### 4.1 线性代数

#### 4.1.1 叉积在行列式中的应用

叉积在行列式中有着重要的应用。行列式是一个方阵的标量值，它反映了方阵的行列关系。利用叉积，我们可以计算三阶方阵的行列式。

**代码块：**

import numpy as np

# 定义一个三阶方阵
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# 计算行列式
det_A = np.linalg.det(A)

# 输出行列式
print("行列式：", det_A)

**逻辑分析：**

该代码块使用 NumPy 库中的 `linalg.det()` 函数计算三阶方阵 `A` 的行列式。行列式的值存储在变量 `det_A` 中，并输出到控制台。

#### 4.1.2 叉积在向量空间中的应用

叉积在向量空间中也发挥着重要作用。向量空间是一个由向量和运算组成的集合。利用叉积，我们可以计算向量空间中的正交基。

**代码块：**

import numpy as np

# 定义两个向量
v1 = np.array([1, 2, 3])
v2 = np.array([4, 5, 6])

# 计算叉积
v3 = np.cross(v1, v2)

# 输出叉积
print("叉积：", v3)

**逻辑分析：**

该代码块使用 NumPy 库中的 `cross()` 函数计算两个向量 `v1` 和 `v2` 的叉积。叉积的结果存储在变量 `v3` 中，并输出到控制台。

### 4.2 物理学

#### 4.2.1 叉积在电磁学中的应用

叉积在电磁学中有着广泛的应用。它可以用于计算磁场和电场。

**代码块：**

import numpy as np

# 定义磁感应强度
B = np.array([0, 1, 0])

# 定义电流密度
J = np.array([1, 0, 0])

# 计算洛伦兹力
F = np.cross(J, B)

# 输出洛伦兹力
print("洛伦兹力：", F)

**逻辑分析：**

该代码块使用 NumPy 库中的 `cross()` 函数计算磁感应强度 `B` 和电流密度 `J` 的叉积，得到洛伦兹力 `F`。洛伦兹力是一个电荷在磁场中受到的力，它的方向垂直于磁场和电流方向。

#### 4.2.2 叉积在流体力学中的应用

叉积在流体力学中也有着重要的应用。它可以用于计算涡旋和流体的速度梯度。

**代码块：**

import numpy as np

# 定义速度场
u = np.array([1, 2, 3])

# 定义位置向量
r = np.array([4, 5, 6])

# 计算涡旋
omega = np.cross(u, r)

# 输出涡旋
print("涡旋：", omega)

**逻辑分析：**

该代码块使用 NumPy 库中的 `cross()` 函数计算速度场 `u` 和位置向量 `r` 的叉积，得到涡旋 `omega`。涡旋是一个流体中旋转流动的度量，它的方向垂直于流体的速度梯度。

# 5. 叉积的计算技巧

### 5.1 手算技巧

#### 5.1.1 行列式法的快速计算

行列式法计算叉积时，可以使用快速计算技巧，即**萨鲁斯法则**。该法则将行列式展开为三个行列式的和，每个行列式包含两个向量中的一个分量和一个常数。

**萨鲁斯法则公式：**

[a1, a2, a3] x [b1, b2, b3] =
a1(b2c3 - b3c2) - a2(b1c3 - b3c1) + a3(b1c2 - b2c1)

**参数说明：**

* `a1`, `a2`, `a3`：向量 `a` 的三个分量
* `b1`, `b2`, `b3`：向量 `b` 的三个分量

**代码块：**

import numpy as np

def cross_product_行列式法(a, b):
    """
    使用行列式法计算叉积。

    参数：
        a (numpy.ndarray): 三维向量 a
        b (numpy.ndarray): 三维向量 b

    返回：
        numpy.ndarray: 三维向量，表示 a 和 b 的叉积
    """
    a1, a2, a3 = a
    b1, b2, b3 = b
    return np.array([
        a1 * (b2 * a3 - b3 * a2),
        -a2 * (b1 * a3 - b3 * a1),
        a3 * (b1 * a2 - b2 * a1)
    ])

**逻辑分析：**

该代码块实现了行列式法计算叉积。它将向量 `a` 和 `b` 的分量代入萨鲁斯法则公式，并返回计算出的叉积向量。

#### 5.1.2 几何法的直观计算

几何法计算叉积时，可以利用直观的方法，即**右手定则**。右手定则规定：将右手大拇指指向向量 `a` 的方向，食指指向向量 `b` 的方向，那么中指指向的向量就是 `a` 和 `b` 的叉积向量。

**右手定则步骤：**

1. 将右手大拇指指向向量 `a` 的方向。
2. 将右手食指指向向量 `b` 的方向。
3. 中指指向的向量就是 `a` 和 `b` 的叉积向量。

### 5.2 程序化计算

#### 5.2.1 Python中的叉积计算

在 Python 中，可以使用 `numpy` 库中的 `cross` 函数计算叉积。该函数接受两个三维向量作为参数，并返回计算出的叉积向量。

**代码块：**

import numpy as np

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
cross_product = np.cross(a, b)
print(cross_product)  # 输出：[-3, 6, -3]

**逻辑分析：**

该代码块使用 `numpy` 库中的 `cross` 函数计算向量 `a` 和 `b` 的叉积，并打印结果。

#### 5.2.2 MATLAB中的叉积计算

在 MATLAB 中，可以使用 `cross` 函数计算叉积。该函数接受两个三维向量作为参数，并返回计算出的叉积向量。

**代码块：**

a = [1, 2, 3];
b = [4, 5, 6];
cross_product = cross(a, b);
disp(cross_product);  % 输出：[-3, 6, -3]

**逻辑分析：**

该代码块使用 MATLAB 中的 `cross` 函数计算向量 `a` 和 `b` 的叉积，并显示结果。

# 6.1 三维空间中的叉积

在三维空间中，叉积是一个二元运算，它将两个向量映射到一个向量。叉积的几何意义是，它生成一个与两个原始向量垂直的向量，其方向由右手定则决定。

叉积的计算公式为：

a × b = |a| |b| sin(θ) n

其中：

* `a` 和 `b` 是两个向量
* `|a|` 和 `|b|` 分别是 `a` 和 `b` 的模长
* `θ` 是 `a` 和 `b` 之间的夹角
* `n` 是与 `a` 和 `b` 垂直的单位向量，其方向由右手定则决定

**右手定则：**

将右手的手指指向 `a` 向量，然后将手指弯曲到 `b` 向量。大拇指指向叉积 `a × b` 的方向。

三维空间中的叉积具有以下性质：

* **反交换性：** `a × b = -b × a`
* **结合性：** `(a × b) × c = a × (b × c)`
* **分配性：** `a × (b + c) = a × b + a × c`
* **标量乘法：** `(k × a) × b = k × (a × b)`，其中 `k` 是一个标量

叉积在三维空间中有着广泛的应用，例如：

* 计算力矩和转动惯量
* 计算面积和体积
* 求解线性方程组
* 模拟物理现象