揭秘点乘算法背后的数学原理：MATLAB点乘的深入分析

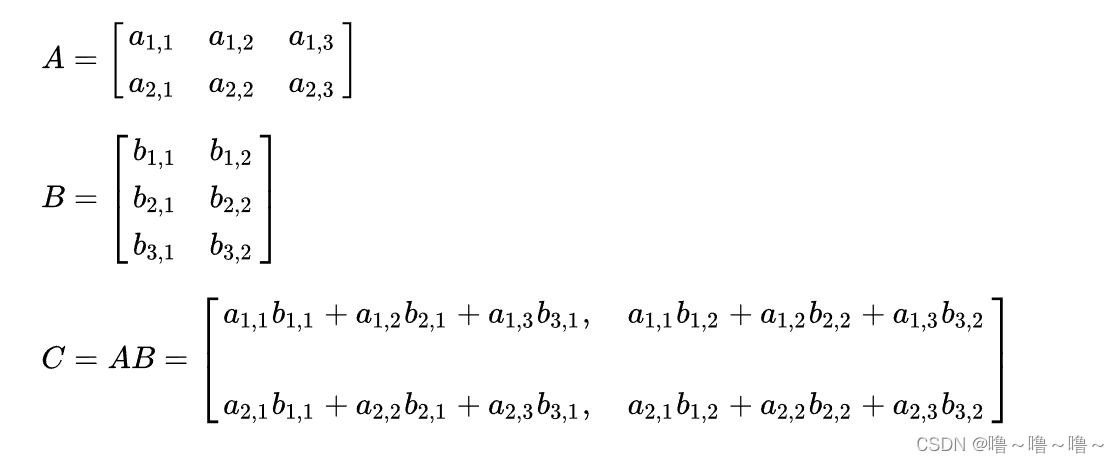
# 1. 点乘算法的数学原理**

**1.1 向量空间与内积**

在数学中，向量空间是一个由向量和标量组成的集合，其中向量可以进行加法和数乘运算。内积是向量空间中两个向量之间的运算，它产生一个标量。

**1.2 点乘的定义与几何意义**

点乘是向量空间中两个向量的内积。对于两个向量 `a = (a1, a2, ..., an)` 和 `b = (b1, b2, ..., bn)`，它们的点乘定义为：

a · b = a1 * b1 + a2 * b2 + ... + an * bn

点乘的几何意义是两个向量在同一方向上的投影的乘积。如果两个向量共线，则它们的点乘为正；如果两个向量正交，则它们的点乘为零。

# 2. MATLAB中的点乘实现

### 2.1 点乘函数的语法和用法

MATLAB中提供了`dot`函数来计算向量的点乘。其语法为：

y = dot(x1, x2)

其中：

- `x1`和`x2`是两个向量，维度必须相同。
- `y`是点乘结果，是一个标量。

例如，计算两个向量`a`和`b`的点乘：

a = [1, 2, 3];
b = [4, 5, 6];
c = dot(a, b)

输出结果为`32`，表示`a`和`b`的点乘结果。

### 2.2 点乘运算的数学基础

#### 2.2.1 矩阵乘法的本质

点乘本质上是矩阵乘法的简化形式。对于两个向量`a`和`b`，可以将其表示为：

a = [a1, a2, ..., an]
b = [b1, b2, ..., bn]

则点乘可以表示为：

a · b = a1 * b1 + a2 * b2 + ... + an * bn

这等价于两个向量的转置相乘：

a · b = a^T * b

#### 2.2.2 点乘与矩阵乘法的联系

点乘是矩阵乘法的一种特殊情况，其中一个矩阵是行向量，另一个矩阵是列向量。在这种情况下，矩阵乘法的结果是一个标量，即点乘结果。

例如，对于行向量`a`和列向量`b`：

a = [1, 2, 3]
b = [4, 5, 6]^T

则点乘可以表示为：

a · b = a * b = [1, 2, 3] * [4, 5, 6]^T = 32

这与使用`dot`函数计算的点乘结果相同。

# 3. 点乘算法的应用

### 3.1 向量投影与正交性

#### 3.1.1 向量投影的公式与几何解释

**向量投影的公式：**

proj_v_u = (v · u / ||u||^2) * u

其中：

* `v` 和 `u` 为两个向量
* `proj_v_u` 为 `v` 在 `u` 方向上的投影向量

**几何解释：**

向量投影的几何解释如下图所示：

[Image of vector projection]

在图中，向量 `v` 可以分解为两个分量：

* 与 `u` 平行的分量，即 `proj_v_u`
* 与 `u` 垂直的分量，即 `v - proj_v_u`

#### 3.1.2 正交向量的判定

两个向量 `v` 和 `u` 正交当且仅当它们的点乘为 0，即：

v · u = 0

这表明 `v` 和 `u` 在几何上相互垂直。

### 3.2 向量间的距离与夹角

#### 3.2.1 向量距离的公式

两个向量 `v` 和 `u` 之间的距离为：

dist(v, u) = ||v - u||

其中：

* `||v - u||` 为向量 `v - u` 的模长

#### 3.2.2 向量夹角的公式

两个向量 `v` 和 `u` 之间的夹角为：