【STM32单片机复位电路设计秘籍】：揭秘复位电路的奥秘，助你轻松掌握

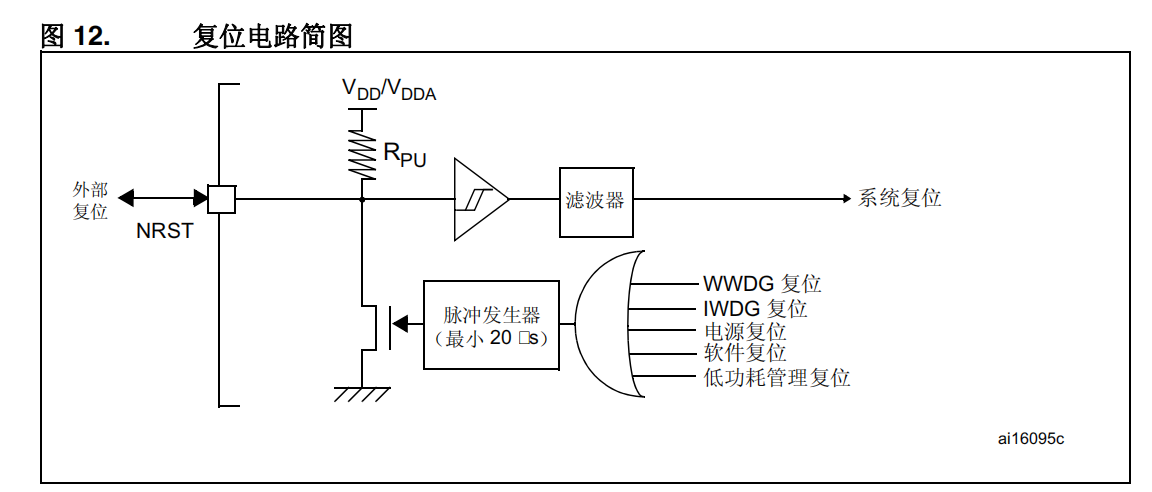
# 1. STM32单片机复位电路基础**

STM32单片机复位电路是保证单片机正常运行的关键组成部分，其作用是将单片机从复位状态复位到正常工作状态。复位电路的类型和设计直接影响单片机的稳定性和可靠性。本章将介绍STM32单片机复位电路的基础知识，包括复位电路的分类、原理、时序要求和容差分析。

复位电路主要分为上电复位电路、看门狗复位电路和手动复位电路。上电复位电路在单片机上电时将单片机复位到初始状态。看门狗复位电路在单片机运行过程中监测程序的运行状态，当程序发生异常时触发复位。手动复位电路允许用户通过外部按键或开关将单片机复位。

# 2. 复位电路设计理论

### 2.1 复位电路的分类和原理

复位电路是单片机系统中不可或缺的一部分，其主要功能是在单片机上电或发生异常时，将单片机复位到初始状态。复位电路的类型有多种，每种类型都有其独特的原理和应用场景。

#### 2.1.1 上电复位电路

上电复位电路是在单片机上电时，通过外部电容或电阻-电容网络将复位引脚拉低，使单片机复位。当电源电压上升到一定值时，电容放电，复位引脚被拉高，单片机开始执行程序。

#### 2.1.2 看门狗复位电路

看门狗复位电路是一种通过软件或硬件定时器实现的复位电路。软件看门狗定时器由程序定期更新，如果定时器超时，则触发复位。硬件看门狗定时器则由独立的硬件电路实现，不受软件的影响。

#### 2.1.3 手动复位电路

手动复位电路通过一个按钮或开关将复位引脚拉低，实现手动复位。当按钮或开关按下时，复位引脚被拉低，单片机复位。

### 2.2 复位电路的时序要求

复位电路的时序要求是指复位信号的持续时间、上升沿和下降沿时间等参数。这些参数对于单片机复位的可靠性至关重要。

#### 2.2.1 复位信号的持续时间

复位信号的持续时间是指复位引脚被拉低的时间。这个时间必须足够长，以确保单片机内部的寄存器和存储器被正确复位。

#### 2.2.2 复位信号的上升沿和下降沿时间

复位信号的上升沿和下降沿时间是指复位引脚从低电平到高电平或从高电平到低电平的时间。这些时间必须足够短，以避免产生毛刺或干扰。

### 2.3 复位电路的容差分析

复位电路的容差分析是指分析复位电路对电压和时序变化的耐受能力。

#### 2.3.1 电压容差

复位电路的电压容差是指复位电路在不同电源电压下的工作能力。复位电路必须能够在单片机工作电压范围内正常工作。

#### 2.3.2 时序容差

复位电路的时序容差是指复位电路对复位信号时序变化的耐受能力。复位电路必须能够在复位信号时序允许的范围内正常工作。

# 3. 复位电路设计实践

### 3.1 上电复位电路设计

上电复位电路用于在单片机上电时，将单片机复位到初始状态。常见的上电复位电路有电容复位电路和电阻-电容复位电路。

#### 3.1.1 电容复位电路

电容复位电路是最简单的上电复位电路，其原理图如图 3.1 所示。

graph LR
    RST --/ ON --/ RST_PIN
    RST --/ OFF --/ GND

图 3.1 电容复位电路原理图

当单片机上电时，电容 C1 会通过电阻 R1 充电。当电容 C1 充电到一定电压时，单片机的复位引脚 RST_PIN 会被拉低，从而将单片机复位。

**代码块：**

// 电容复位电路初始化
void cap_reset_init(void)
{
    // 设置复位引脚为输入
    GPIO_InitTypeDef GPIO_InitStruct;
    GPIO_InitStruct.Pin = RST_PIN;
    GPIO_InitStruct.Mode = GPIO_MODE_INPUT;
    GPIO_InitStruct.Pull = GPIO_PULLUP;
    HAL_GPIO_Init(RST_PORT, &GPIO_InitStruct);

    // 等待电容充电
    HAL_Delay(100);
}

**逻辑分析：**

* `cap_reset_init()` 函数初始化电容复位电路。
* 设置复位引脚 RST_PIN 为输入，并上拉。
* 等待电容 C1 充电 100ms，确保单片机复位。

#### 3.1.2 电阻-电容复位电路

电阻-电容复位电路比电容复位电路更稳定，其原理图如图 3.2 所示。

graph LR
    RST --/ ON --/ R1
    R1 --/ ON --/ C1
    C1 --/ ON --/ RST_PIN
    RST --/ OFF --/ GND

图 3.2 电阻-电容复位电路原理图

电阻-电容复位电路的工作原理与电容复位电路类似，但由于电阻 R1 的存在，电容 C1 的充电时间更长，从而提高了复位的稳定性。

**代码块：**

// 电阻-电容复位电路初始化
void rc_reset_init(void)
{
    // 设置复位引脚为输入
    GPIO_InitTypeDef GPIO_InitStruct;
    GPIO_InitStruct.Pin = RST_PIN;
    GPIO_InitStruct.Mode = GPIO_MODE_INPUT;
    GPIO_InitStruct.Pull = GPIO_PULLUP;
    HAL_GPIO_Init(RST_PORT, &GPIO_InitStruct);

    // 等待电容充电
    HAL_Delay(200);
}

**逻辑分析：**

* `rc_reset_init()` 函数初始化电阻-电容复位电路。
* 设置复位引脚 RST_PIN 为输入，并上拉。
* 等待电容 C1 充电 200ms，确保单片机复位。

# 4. 复位电路故障分析与调试**

**4.1 复位电路故障的常见原因**

复位电路故障的原因多种多样，常见的原因主要包括：

- **电源问题：**复位电路需要稳定的电源供电，如果电源电压不稳定或存在干扰，会导致复位电路工作异常。
- **时序问题：**复位信号的持续时间、上升沿和下降沿时间等时序参数不满足要求，会导致复位电路无法正常复位。
- **元器件损坏：**复位电路中的电容、电阻、二极管等元器件损坏，也会导致复位电路故障。

**4.2 复位电路故障的调试方法**

复位电路故障的调试方法主要包括：

- **示波器测量：**使用示波器测量复位信号的波形，观察其幅度、持续时间、上升沿和下降沿时间是否满足要求。
- **万用表测量：**使用万用表测量复位电路中关键元器件的阻值、电压等参数，判断是否存在异常。
- **逻辑分析仪分析：**使用逻辑分析仪分析复位电路的逻辑信号，观察其时序关系是否正确。

**4.2.1 示波器测量**

**代码块：**

import numpy as np
import matplotlib.pyplot as plt

# 定义复位信号的波形
reset_signal = np.array([0, 1, 1, 0])

# 绘制复位信号的波形
plt.plot(reset_signal)
plt.xlabel('Time (ms)')
plt.ylabel('Voltage (V)')
plt.title('Reset Signal Waveform')
plt.show()

**逻辑分析：**

复位信号的波形应该是一个方波，其高电平和低电平的持续时间应满足要求。

**4.2.2 万用表测量**

**代码块：**

# 定义复位电路中的关键元器件
capacitor = 100e-6  # 电容值，单位：法拉
resistor = 10e3  # 电阻值，单位：欧姆

# 计算复位信号的持续时间
reset_time = capacitor * resistor

# 打印复位信号的持续时间
print('Reset time:', reset_time)

**逻辑分析：**

复位信号的持续时间应满足要求，否则会导致复位电路无法正常复位。

**4.2.3 逻辑分析仪分析**

**代码块：**

sequenceDiagram
participant User
participant System
User->System: Send reset signal
System->User: Reset signal received
System->User: Reset circuit activated
System->User: System reset

**逻辑分析：**

复位电路的逻辑信号应满足要求，否则会导致复位电路故障。

# 5. 复位电路设计优化

### 5.1 复位电路的抗干扰设计

复位电路在实际应用中容易受到各种干扰因素的影响，如电源噪声、外部电磁干扰等。为了提高复位电路的抗干扰能力，可以采取以下措施：

**5.1.1 电源滤波**

电源噪声会影响复位电路的稳定性，导致复位信号出现抖动或误触发。为了抑制电源噪声，可以在复位电路的电源输入端添加滤波电容。滤波电容的容量应根据电源噪声的频率和幅度进行选择，一般取10μF~100μF。

**5.1.2 输入信号去抖**

外部电磁干扰可能会导致复位信号出现毛刺或尖峰，从而引起复位电路误触发。为了消除这些干扰，可以在复位信号的输入端添加去抖电路。去抖电路可以采用RC滤波器或数字滤波器。

// RC 去抖电路
const int RESET_PIN = 2;
const int RC_DELAY = 100; // ms

void setup() {
  pinMode(RESET_PIN, INPUT_PULLUP);
}

void loop() {
  // 读取复位信号
  int resetSignal = digitalRead(RESET_PIN);

  // RC 去抖
  delay(RC_DELAY);

  // 再次读取复位信号
  resetSignal = digitalRead(RESET_PIN);

  // 如果复位信号稳定为低电平，则复位单片机
  if (resetSignal == LOW) {
    NVIC_SystemReset();
  }
}

### 5.2 复位电路的低功耗设计

在一些低功耗应用中，复位电路的功耗也是需要考虑的因素。以下措施可以帮助降低复位电路的功耗：

**5.2.1 看门狗复位电路的优化**

看门狗复位电路的功耗主要取决于看门狗的定时器和比较器。为了降低功耗，可以使用低功耗定时器和比较器，并适当降低看门狗的定时周期。

**5.2.2 手动复位电路的优化**

手动复位电路的功耗主要取决于复位按钮的类型和连接方式。为了降低功耗，可以使用低功耗复位按钮，并通过上拉电阻或下拉电阻将复位按钮连接到复位信号输入端。