揭秘MATLAB图像处理中的傅里叶变换：理解图像频域，解锁图像处理新境界

# 1. 图像处理中的傅里叶变换概述

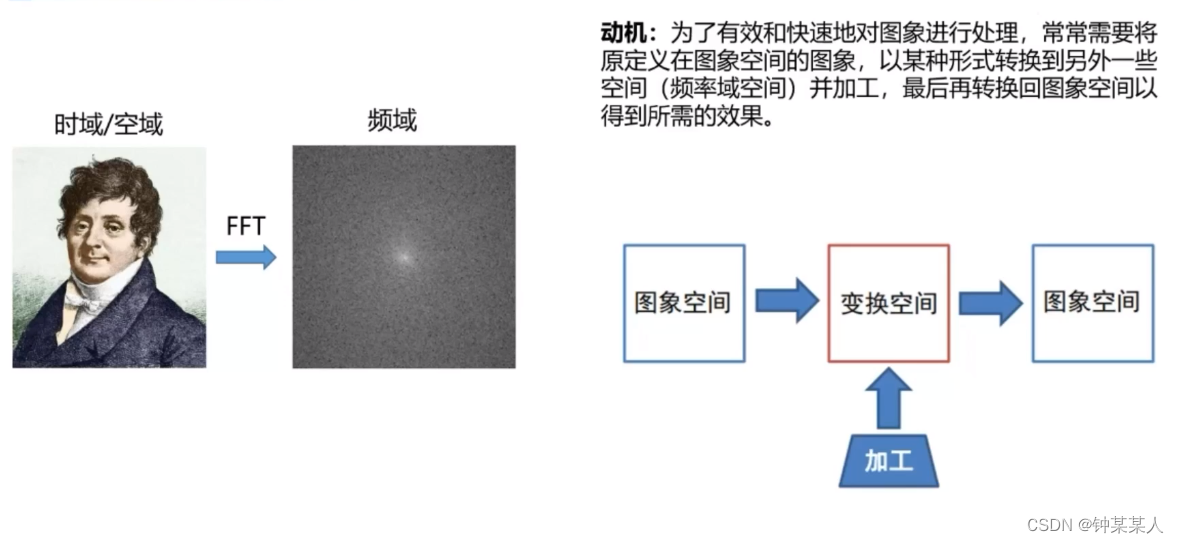
傅里叶变换是一种数学工具，用于将信号（如图像）从时域（空间域）转换为频域。在图像处理中，傅里叶变换可用于分析图像的频率成分，从而实现图像滤波、增强和分析等操作。

傅里叶变换将图像分解为一系列正弦和余弦波，每个波都有特定的频率和幅度。图像中不同频率的成分对应于图像的不同特征，例如边缘、纹理和噪声。通过操纵傅里叶变换，我们可以选择性地增强或抑制图像中的特定频率成分，从而实现图像处理的目标。

# 2. 傅里叶变换的理论基础

### 2.1 傅里叶级数和傅里叶变换

**傅里叶级数**

傅里叶级数是一种将周期函数表示为正弦和余弦函数之和的数学工具。对于一个周期为 `T` 的周期函数 `f(t)`，其傅里叶级数表示为：

f(t) = a_0 + ∑[n=1,∞] (a_n cos(2πnt/T) + b_n sin(2πnt/T))

其中，`a_0`、`a_n` 和 `b_n` 是傅里叶系数，可以通过以下积分计算得到：

a_0 = (1/T) ∫[0,T] f(t) dt
a_n = (2/T) ∫[0,T] f(t) cos(2πnt/T) dt
b_n = (2/T) ∫[0,T] f(t) sin(2πnt/T) dt

**傅里叶变换**

傅里叶变换是傅里叶级数在非周期函数上的推广。对于一个非周期函数 `f(t)`，其傅里叶变换定义为：

F(ω) = ∫[−∞,∞] f(t) e^(-iωt) dt

其中，`ω` 是角频率。

傅里叶变换将时域信号 `f(t)` 转换为频域信号 `F(ω)`，其中 `F(ω)` 表示信号在不同频率下的幅度和相位信息。

### 2.2 傅里叶变换的性质和应用

傅里叶变换具有以下重要性质：

* **线性性：**傅里叶变换是线性的，即对于任意常数 `a` 和 `b`，以及函数 `f(t)` 和 `g(t)`，有 `F(af(t) + bg(t)) = aF(f(t)) + bF(g(t))`。
* **时移：**如果 `f(t)` 时移 `t_0`，则 `F(ω)` 相移 `-ωt_0`。
* **频率缩放：**如果 `f(t)` 频率缩放 `a` 倍，则 `F(ω)` 也缩放 `a` 倍。
* **卷积定理：**两个函数 `f(t)` 和 `g(t)` 的卷积 `f(t) * g(t)` 的傅里叶变换等于 `F(ω) * G(ω)`。

傅里叶变换在信号处理、图像处理、通信等领域有着广泛的应用。例如：

* **频谱分析：**傅里叶变换可以将信号分解为不同频率的成分，从而进行频谱分析。
* **滤波：**傅里叶变换可以用于设计滤波器，去除信号中的特定频率成分。
* **图像增强：**傅里叶变换可以用于图像增强，例如锐化和对比度增强。
* **图像配准：**傅里叶变换可以用于图像配准，即将两幅图像对齐。

# 3. 傅里叶变换在图像处理中的实践

### 3.1 图像的傅里叶变换和逆变换

**图像的傅里叶变换**

图像的傅里叶变换将图像从空间域转换为频率域。它通过计算图像中每个像素的频率分量来实现。傅里叶变换公式如下：

F(u, v) = ∑∑ f(x, y) e^(-j2π(ux + vy))

其中：

* `F(u, v)` 是图像的傅里叶变换
* `f(x, y)` 是图像的像素值
* `u` 和 `v` 是频率变量

**图像的逆傅里叶变换**

图像的逆傅里叶变换将图像从频率域转换回空间域。它通过计算图像中每个像素的复数指数和来实现。逆傅里叶变换公式如下：

f(x, y) = 1/(MN) ∑∑ F(u, v) e^(j2π(ux + vy))

其中：

* `f(x, y)` 是图像的逆傅里叶变换
* `F(u, v)` 是图像的傅里叶变换
* `M` 和 `N` 是图像的宽度和高度

### 3.2 傅里叶变换在图像滤波中的应用

傅里叶变换在图像滤波中有着广泛的应用。通过在频率域中操作图像，我们可以实现各种滤波效果。

#### 3.2.1 低通滤波器和高通滤波器

**低通滤波器**

低通滤波器可以去除图像中的高频分量，从而平滑图像。低通滤波器的频率响应如下图所示：

[图片：低通滤波器的频率响应]

**高通滤波器**

高通滤波器可以去除图像中的低频分量，从而增强图像的边缘和细节。高通滤波器的频率响应如下图所示：

[图片：高通滤波器的频率响应]

#### 3.2.2 滤波器设计和实现

图像滤波器的设计和实现需要考虑以下步骤：

1. **确定滤波器类型：**根据需要去除或保留的频率分量选择低通滤波器或高通滤波器。
2. **设计滤波器内核：**滤波器内核是一个二维矩阵，用于卷积图像。内核的权重决定了滤波器的频率响应。
3. **应用滤波器：**将滤波器内核与图像卷积，得到滤波后的图像。

### 3.3 傅里叶变换在图像增强中的应用

傅里叶变换还可以用于图像增强，包括图像锐化和对比度增强。

#### 3.3.1 图像锐化

图像锐化可以增强图像的边缘和细节。通过在频率域中增强图像的高频分量可以实现图像锐化。

#### 3.3.2 图像对比度增强

图像对比度增强可以增加图像中不同区域之间的差异。通过调整图像的傅里叶变换的幅度谱可以实现图像对比度增强。

# 4. 傅里叶变换在图像分析中的应用

傅里叶变换在图像分析中扮演着至关重要的角色，它为图像的频谱分析、配准和融合提供了强大的工具。

### 4.1 图像频谱分析

图像频谱是傅里叶变换的幅度谱，它揭示了图像中不同频率分量的分布。通过分析频谱，我们可以获得有关图像纹理、边缘和噪声等特征的宝贵信息。

**代码块：**

import numpy as np
import matplotlib.pyplot as plt

# 加载图像
image = plt.imread('image.jpg')

# 计算傅里叶变换
fft_image = np.fft.fft2(image)

# 计算幅度谱
amplitude_spectrum = np.abs(fft_image)

# 显示幅度谱
plt.imshow(amplitude_spectrum, cmap='gray')
plt.show()

**逻辑分析：**

* `np.fft.fft2(image)`：计算图像的二维傅里叶变换，结果存储在 `fft_image` 中。
* `np.abs(fft_image)`：计算傅里叶变换的幅度谱，结果存储在 `amplitude_spectrum` 中。
* `plt.imshow(amplitude_spectrum, cmap='gray')`：显示幅度谱，使用灰度颜色映射。

### 4.2 图像配准和图像融合

傅里叶变换还可以用于图像配准和图像融合。图像配准是指将两幅或多幅图像对齐，使其具有相同的几何变换。图像融合是指将两幅或多幅图像组合成一幅新的图像，该图像包含所有输入图像的特征。

**图像配准：**

* 使用傅里叶变换将两幅图像转换为频域。
* 计算两幅图像频谱之间的相位差。
* 通过相位差计算图像之间的几何变换。

**图像融合：**

* 使用傅里叶变换将两幅图像转换为频域。
* 选择要融合的频谱区域。
* 将选定的频谱区域融合在一起。
* 使用逆傅里叶变换将融合后的频谱转换为空间域。

**代码块：**

import numpy as np
import cv2

# 加载图像
image1 = cv2.imread('image1.jpg')
image2 = cv2.imread('image2.jpg')

# 计算傅里叶变换
fft_image1 = np.fft.fft2(image1)
fft_image2 = np.fft.fft2(image2)

# 计算相位差
phase_diff = np.angle(fft_image1) - np.angle(fft_image2)

# 计算几何变换
transform = cv2.estimateRigidTransform(phase_diff, np.zeros_like(phase_diff))

# 配准图像
aligned_image = cv2.warpAffine(image1, transform, (image1.shape[1], image1.shape[0]))

**逻辑分析：**

* `np.fft.fft2(image1)` 和 `np.fft.fft2(image2)`：计算两幅图像的二维傅里叶变换。
* `np.angle(fft_image1) - np.angle(fft_image2)`：计算两幅图像频谱之间的相位差。
* `cv2.estimateRigidTransform(phase_diff, np.zeros_like(phase_diff))`：计算图像之间的几何变换。
* `cv2.warpAffine(image1, transform, (image1.shape[1], image1.shape[0]))`：使用几何变换配准图像。

# 5. MATLAB中傅里叶变换的实现和应用

### 5.1 MATLAB中傅里叶变换函数

MATLAB提供了丰富的傅里叶变换函数，其中最常用的包括：

- `fft`：离散傅里叶变换（DFT）
- `ifft`：逆离散傅里叶变换（IDFT）
- `fftshift`：将零频分量移到频谱中心
- `ifftshift`：将零频分量移回频谱起始位置

### 5.2 MATLAB中图像傅里叶变换的实例

以下代码演示了如何使用MATLAB对图像进行傅里叶变换：

% 读取图像
image = imread('image.jpg');

% 将图像转换为灰度图像
image_gray = rgb2gray(image);

% 计算图像的傅里叶变换
F = fft2(image_gray);

% 将零频分量移到频谱中心
F_shifted = fftshift(F);

% 显示傅里叶变换后的频谱
figure;
imshow(log(abs(F_shifted)), []);
title('图像傅里叶变换频谱');

### 5.3 MATLAB中傅里叶变换在图像处理中的应用示例

MATLAB中的傅里叶变换函数可以广泛应用于图像处理，以下是一些示例：

**图像滤波**

% 创建一个高通滤波器
H = fspecial('gaussian', [5 5], 2);

% 将滤波器应用于图像傅里叶变换
F_filtered = F .* H;

% 执行逆傅里叶变换
image_filtered = ifft2(F_filtered);

% 将零频分量移回频谱起始位置
image_filtered = ifftshift(image_filtered);

% 显示滤波后的图像
figure;
imshow(image_filtered, []);
title('高通滤波后的图像');

**图像增强**

% 创建一个锐化滤波器
H = fspecial('unsharp', 0.5);

% 将滤波器应用于图像傅里叶变换
F_sharpened = F .* H;

% 执行逆傅里叶变换
image_sharpened = ifft2(F_sharpened);

% 将零频分量移回频谱起始位置
image_sharpened = ifftshift(image_sharpened);

% 显示锐化后的图像
figure;
imshow(image_sharpened, []);
title('锐化后的图像');