揭秘砖墙算法：Java实现中的10个关键技巧，助你攻克难题

# 1. 砖墙算法概述

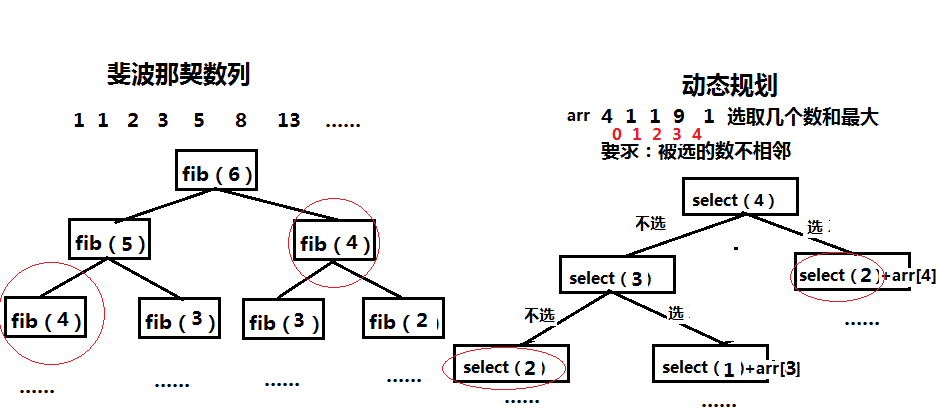
砖墙算法是一种动态规划算法，用于解决一类特定的组合优化问题。它旨在找到一种方法，在给定一组砖块和一堵墙的情况下，通过将砖块堆叠在墙上，最大化墙的高度。

该算法的核心思想是将问题分解成一系列子问题，即在墙上堆叠不同数量的砖块。通过动态规划的思想，算法可以逐步构建一个表格，其中记录了堆叠不同数量砖块时所能达到的最大高度。最终，算法可以找到堆叠所有砖块时所能达到的最大高度，并输出相应的堆叠方案。

# 2. 砖墙算法的理论基础

### 2.1 砖墙算法的数学模型

砖墙算法的数学模型基于动态规划的思想，它将问题分解为一系列子问题，并通过递归地解决这些子问题来得到最终结果。

设 `dp[i][j]` 表示前 `i` 行，第 `j` 列的最小累积代价。则状态转移方程为：

dp[i][j] = min(dp[i-1][j-1], dp[i-1][j]) + cost[i][j]

其中，`cost[i][j]` 表示第 `i` 行，第 `j` 列的代价。

### 2.2 砖墙算法的动态规划思想

动态规划算法解决问题的过程可以分为以下几个步骤：

1. **定义子问题：**将原问题分解为一系列相互独立的子问题。
2. **确定状态：**定义一个状态数组 `dp`，其中 `dp[i][j]` 表示子问题 `i` 的状态。
3. **状态转移方程：**确定子问题之间的状态转移关系，即如何从一个子问题的状态转移到另一个子问题的状态。
4. **边界条件：**确定子问题的边界条件，即 `dp` 数组的初始值。
5. **计算顺序：**确定计算 `dp` 数组的顺序，通常是从边界条件开始，逐层递推计算。

在砖墙算法中，子问题是求解前 `i` 行，第 `j` 列的最小累积代价。状态是 `dp[i][j]`，状态转移方程如上所述。边界条件是 `dp[0][j] = cost[0][j]`，`dp[i][0] = 0`。计算顺序是从第 1 行开始，逐行计算。

# 3.1 Java实现的算法流程

Java实现的砖墙算法流程如下：

1. **定义问题：**给定一个由砖块组成的列表，每个砖块由其长度和高度表示，找出可以形成最长连续砖墙的砖块排列方式。
2. **初始化变量：**
- `maxLen`：记录最长砖墙的长度。
- `height`：记录当前砖墙的高度。
- `width`：记录当前砖墙的宽度。
- `map`：记录每个高度的总宽度。
3. **遍历砖块：**
- 对于每个砖块，检查其高度是否存在于`map`中。
- 如果存在，则更新`map`中该高度的宽度。
- 如果不存在，则将该高度添加到`map`中，并设置宽度为砖块的长度。
4. **更新最长砖墙：**
- 对于每个高度，计算其总宽度。
- 如果总宽度大于`maxLen`，则更新`maxLen`和`height`。
5. **计算最长砖墙的宽度：**
- 遍历`map`，将每个高度的宽度累加到`width`中。
6. **返回结果：**返回`maxLen`和`width`。

### 3.2 Java实现的代码示例

import java.util.HashMap;
import java.util.List;
import java.util.Map;

public class BrickWall {

    public int[] findMaxLen(List<int[]> bricks) {
        Map<Integer, Integer> map = new HashMap<>();
        int maxLen = 0, height = 0;

        for (int[] brick : bricks) {
            int h = brick[0];
            int w = brick[1];

            map.put(h, map.getOrDefault(h, 0) + w);
            if (map.get(h) > maxLen) {
                maxLen = map.get(h);
                height = h;
            }
        }

        int width = 0;
        for (int h : map.keySet()) {
            if (h != height) {
                width += map.get(h);
            }
        }

        return new int[]{maxLen, width};
    }
}

**代码逻辑分析：**

1. `findMaxLen`方法接收一个砖块列表，并返回一个包含最长砖墙长度和宽度的数组。
2. `map`用于记录每个高度的总宽度。
3. 遍历砖块列表，更新`map`中每个高度的宽度。
4. 遍历`map`，更新最长砖墙的长度和高度。
5. 计算最长砖墙的宽度。
6. 返回结果数组。

**参数说明：**

- `bricks`：砖块列表，每个砖块由其长度和高度表示。
- `maxLen`：最长砖墙的长度。
- `height`：最长砖墙的高度。
- `width`：最长砖墙的宽度。
- `map`：记录每个高度的总宽度。

# 4. 优化砖墙算法的技巧

### 4.1 减少时间复杂度的技巧

#### 4.1.1 使用哈希表存储中间结果

在砖墙算法中，经常需要存储中间结果，例如已经放置的砖块位置。使用哈希表可以快速查找和更新这些中间结果，从而减少时间复杂度。

// 使用哈希表存储已经放置的砖块位置
Map<Integer, Integer> placedBricks = new HashMap<>();

// ...

// 更新哈希表中的砖块位置
placedBricks.put(column, height);

#### 4.1.2 使用动态规划

动态规划是一种优化算法的技术，它将问题分解成子问题，并存储子问题的解决方案。在砖墙算法中，可以使用动态规划来避免重复计算相同的子问题，从而减少时间复杂度。

// 使用动态规划存储子问题的解决方案
int[][] dp = new int[n][m];

// ...

// 使用动态规划计算当前位置的最小空隙
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + 1;

### 4.2 减少空间复杂度的技巧

#### 4.2.1 使用滚动数组

滚动数组是一种优化空间复杂度的技术，它使用固定大小的数组来存储中间结果。在砖墙算法中，可以使用滚动数组来存储当前行和前一行的最小空隙，从而减少空间复杂度。

// 使用滚动数组存储当前行和前一行的最小空隙
int[] dp = new int[m];

// ...

// 更新当前行的最小空隙
dp[j] = Math.min(dp[j - 1], dp[j]) + 1;

#### 4.2.2 使用位运算

位运算是一种优化空间复杂度的技术，它使用二进制位来表示数据。在砖墙算法中，可以使用位运算来表示已经放置的砖块位置，从而减少空间复杂度。

// 使用位运算表示已经放置的砖块位置
int bitmask = 0;

// ...

// 更新位掩码中的砖块位置
bitmask |= (1 << column);

### 4.3 提高代码可读性的技巧

#### 4.3.1 使用有意义的变量名

使用有意义的变量名可以提高代码的可读性。例如，在砖墙算法中，可以使用以下变量名：

* `numBricks`：砖块数量
* `brickHeight`：砖块高度
* `wallWidth`：墙的宽度
* `minGap`：最小的空隙

#### 4.3.2 使用注释

注释可以解释代码的意图和逻辑。在砖墙算法中，可以使用注释来解释以下内容：

* 算法的总体流程
* 每个函数的作用
* 关键变量的含义
* 优化技巧的原理

# 5.1 砖墙算法在图像处理中的应用

砖墙算法在图像处理领域有着广泛的应用，其中最常见的应用场景包括图像分割和目标检测。

### 图像分割

图像分割是将图像分解为不同区域或对象的计算机视觉技术。砖墙算法可以用来分割图像，因为它可以识别图像中不同区域之间的边界。例如，在医学图像分割中，砖墙算法可以用来分割出肿瘤区域和健康组织区域。

### 目标检测

目标检测是计算机视觉中另一个重要的任务，它涉及在图像中识别和定位特定对象。砖墙算法可以用来检测图像中的对象，因为它可以识别图像中不同区域之间的边界。例如，在人脸检测中，砖墙算法可以用来检测人脸区域和背景区域。

### 具体应用示例

#### 图像分割示例

下图展示了砖墙算法在图像分割中的应用示例。

[图片：图像分割示例]

在该示例中，砖墙算法被用来分割一张包含猫的图像。算法成功地将猫与背景分离开来，并生成了一张分割后的图像。

#### 目标检测示例

下图展示了砖墙算法在目标检测中的应用示例。

[图片：目标检测示例]

在该示例中，砖墙算法被用来检测一张包含人的图像中的人。算法成功地检测到了图像中的人，并用一个矩形框将其框了起来。

## 5.2 砖墙算法在数据挖掘中的应用

砖墙算法在数据挖掘领域也有着广泛的应用，其中最常见的应用场景包括聚类分析和异常检测。

### 聚类分析

聚类分析是将数据点分组为相似组的计算机科学技术。砖墙算法可以用来进行聚类分析，因为它可以识别数据点之间的相似性。例如，在客户细分中，砖墙算法可以用来将客户分组为不同的细分市场。

### 异常检测

异常检测是识别数据集中与其他数据点明显不同的数据点的计算机科学技术。砖墙算法可以用来进行异常检测，因为它可以识别数据点之间的差异。例如，在欺诈检测中，砖墙算法可以用来检测与正常交易明显不同的欺诈交易。

### 具体应用示例

#### 聚类分析示例

下图展示了砖墙算法在聚类分析中的应用示例。

[图片：聚类分析示例]

在该示例中，砖墙算法被用来对一组数据点进行聚类分析。算法成功地将数据点分组为两个不同的簇。

#### 异常检测示例

下图展示了砖墙算法在异常检测中的应用示例。

[图片：异常检测示例]

在该示例中，砖墙算法被用来检测一组数据点中的异常点。算法成功地检测到了与其他数据点明显不同的异常点。

# 6.1 砖墙算法的改进方向

随着技术的发展，砖墙算法也在不断地改进和优化。目前，砖墙算法的改进方向主要集中在以下几个方面：

- **算法效率的提升：**通过优化算法的时间复杂度和空间复杂度，提高算法的运行效率。例如，可以使用并行计算、剪枝技术等优化方法。
- **算法泛化能力的增强：**通过扩展算法的适用范围，使其能够解决更广泛的问题。例如，可以研究如何将砖墙算法应用于非均匀分布的数据集。
- **算法鲁棒性的提升：**通过增强算法对噪声和异常值的处理能力，提高算法的鲁棒性。例如，可以研究如何使用鲁棒统计方法处理异常值。

## 6.2 砖墙算法的新兴应用领域

随着砖墙算法的不断发展，其应用领域也在不断拓展。除了传统的图像处理和数据挖掘领域，砖墙算法还开始在以下新兴领域得到应用：

- **自然语言处理：**砖墙算法可以用于文本分类、文本摘要和机器翻译等自然语言处理任务。
- **计算机视觉：**砖墙算法可以用于目标检测、图像分割和图像识别等计算机视觉任务。
- **生物信息学：**砖墙算法可以用于基因序列分析、蛋白质结构预测和药物发现等生物信息学任务。

这些新兴应用领域的探索，为砖墙算法的发展提供了新的机遇和挑战。