MATLAB数值计算：掌握数值方法，解决复杂问题

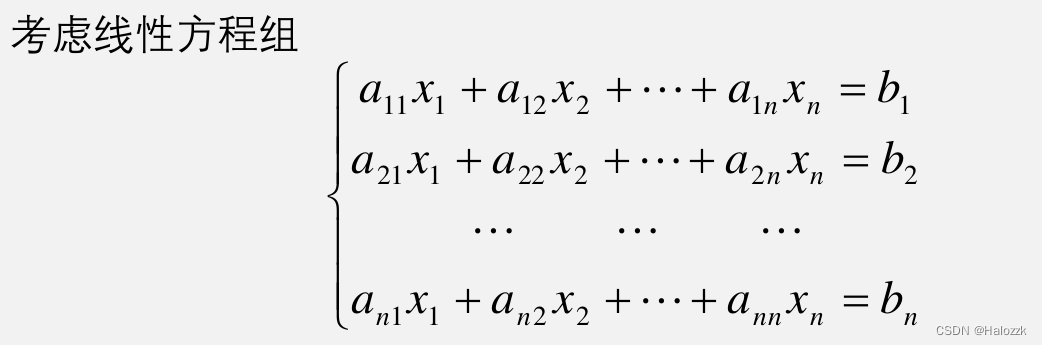
# 1. 数值计算的基础**

数值计算是计算机科学中一个重要的分支，它涉及使用计算机来解决数学问题。数值计算的基础是数值方法，它提供了一系列近似求解连续数学问题的技术。

数值方法通常涉及将连续问题离散化，即将其分解为一系列离散的步骤。然后，这些步骤可以由计算机执行，以产生问题的近似解。数值方法的精度取决于离散化的细度，并且可以通过增加离散化的数量来提高精度。

# 2. 数值方法

数值方法是解决数学问题的近似计算方法，在计算机科学和工程领域有着广泛的应用。本章将介绍几种常用的数值方法，包括迭代法、插值法和数值积分。

### 2.1 迭代法

迭代法是一种通过重复应用一个函数来逼近问题的解的方法。在每次迭代中，函数都会使用前一次迭代的结果作为输入，从而逐步逼近解。

#### 2.1.1 二分法

二分法用于求解在给定区间内连续函数的根。该方法通过不断将区间二等分并测试函数在区间端点的值，来缩小根的范围。

**算法步骤：**

1. 给定函数 f(x) 和区间 [a, b]，其中 f(a) 和 f(b) 异号。
2. 计算中点 c = (a + b) / 2。
3. 如果 f(c) = 0，则 c 是根。
4. 如果 f(c) 和 f(a) 异号，则根在区间 [a, c] 中。否则，根在区间 [c, b] 中。
5. 重复步骤 2-4，直到区间长度小于给定的容差。

**代码块：**

def bisection(f, a, b, tol):
    """
    使用二分法求解函数 f(x) 在区间 [a, b] 内的根。

    参数：
        f: 待求根的函数。
        a: 区间左端点。
        b: 区间右端点。
        tol: 容差。

    返回：
        根的近似值。
    """
    while abs(b - a) > tol:
        c = (a + b) / 2
        if f(c) == 0:
            return c
        elif f(c) * f(a) < 0:
            b = c
        else:
            a = c
    return (a + b) / 2

**逻辑分析：**

代码首先检查函数在区间端点的值是否异号，如果异号，则根存在于该区间内。然后，代码计算区间中点并检查函数在中点处的值。如果函数在中点处为零，则中点即为根。否则，代码根据函数在中点处的值和区间端点的值来确定根所在的区间，并重复该过程，直到区间长度小于给定的容差。

#### 2.1.2 牛顿法

牛顿法用于求解一元方程 f(x) = 0。该方法通过使用函数的导数来构造一个迭代公式，每次迭代都将前一次迭代的结果作为输入，并向函数的根方向移动。

**算法步骤：**

1. 给定函数 f(x) 和其导数 f'(x)。
2. 选择一个初始值 x0。
3. 计算 x1 = x0 - f(x0) / f'(x0)。
4. 重复步骤 3，直到 |x1 - x0| < tol。

**代码块：**

def newton(f, fprime, x0, tol):
    """
    使用牛顿法求解方程 f(x) = 0。

    参数：
        f: 待求解的方程。
        fprime: 方程的导数。
        x0: 初始值。
        tol: 容差。

    返回：
        方程的根的近似值。
    """
    x1 = x0 - f(x0) / fprime(x0)
    while abs(x1 - x0) > tol:
        x0 = x1
        x1 = x0 - f(x0) / fprime(x0)
    return x1

**逻辑分析：**

代码首先计算函数在初始值处的导数值，然后使用牛顿迭代公式更新初始值。代码重复该过程，直到迭代值之间的差值小于给定的容差。

### 2.2 插值法

插值法用于根据一组已知数据点构造一个函数，该函数可以用来估计其他未知数据点的值。

#### 2.2.1 线性插值

线性插值是最简单的插值方法，它使用两条相邻数据点之间的直线来估计未知数据点的值。

**算法步骤：**

1. 给定一组数据点 (x1, y1), (x2, y2), ..., (xn, yn)。
2. 对于未知数据点 x，计算其对应的 y 值：

y = y1 + (x - x1) * (y2 - y1) / (x2 - x1)

**代码块：**

def linear_interpolation(x, y, x_new):
    """
    使用线性插值估计未知数据点 x_new 的值。

    参数：
        x: 已知数据点的 x 坐标。
        y: 已知数据点的 y 坐标。
        x_new: 待估计数据点的 x 坐标。

    返回：
        待估计数据点的 y 坐标的估计值。
    """
    for i in range(len(x) - 1):
        if x[i] <= x_new <= x[i+1]:
            return y[i] + (x_new - x[i]) * (y[i+1] - y[i]) / (x[i+1] - x[i])
    return None

**逻辑分析：**

代码遍历已知数据点，找到与未知数据点 x_new 相邻的两条数据点。然后，代码使用线性插值公式计算未知数据点 y 值的估计值。

#### 2.2.2 多项式插值

多项式插值使用一个多项式函数来拟合已知数据点。该多项式函数可以用来估计未知数据点的值。

**算法步骤：**

1. 给定一组数据点 (x1, y1), (x2, y2), ..., (xn, yn)。
2. 构造一个 n 次多项式 f(x)，使得 f(xi) = yi，i = 1, 2, ..., n。
3. 对于未知数据点 x，计算其对应的 y 值：

y = f(x)

**代码块：**

import numpy as np

def polynomial_interpolation(x, y, x_new):
    """
    使用多项式插值估计未知数据点 x_new 的值。

    参数：
        x: 已知数据点的 x 坐标。
        y: 已知数据点的 y 坐标。
        x_new: 待估计数据点的 x 坐标。

    返回：