R语言网络分析：图论与社交网络分析入门指南

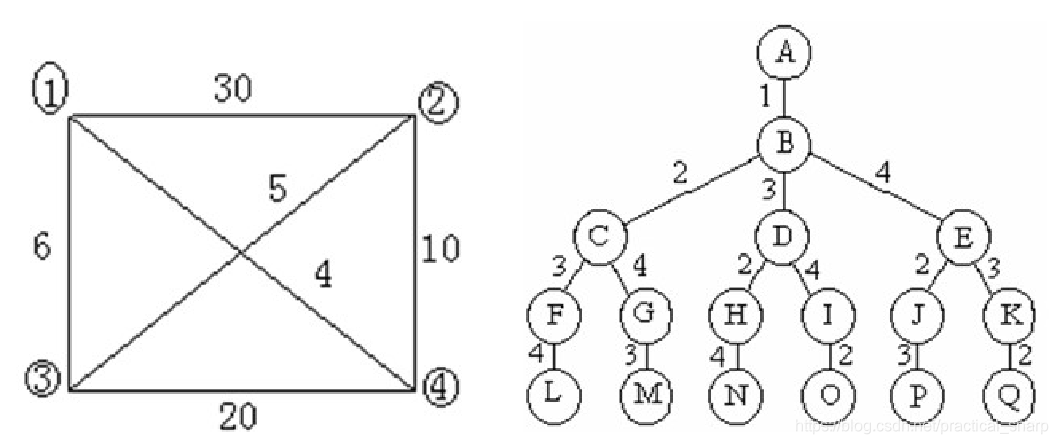
# 1. R语言网络分析概述

随着大数据时代的到来，网络分析已成为数据科学领域中不可或缺的一部分，尤其在社会网络分析、生物网络研究、互联网技术等领域。R语言作为一款强大的统计分析软件，其在图形和网络分析方面的包和函数日益丰富，为网络分析带来了极大的便利和可能性。

网络分析不仅仅关注节点（即网络中的个体），还关注节点间的连接（即关系或交互）。在这一章节中，我们将首先简要介绍网络分析在R语言中的应用背景、基础概念以及研究意义。然后，我们将详细探讨R语言在网络分析中的优势和常用工具，为读者提供一个全面的基础知识框架，帮助读者对后续章节中的图论基础、社交网络分析等复杂主题有一个深入理解的起点。

在接下来的章节中，我们将通过实际案例和深入的代码实践，让读者进一步掌握如何使用R语言进行各种网络分析，包括社交网络的构建、社区检测、影响力分析等。这一切将从第一章的网络分析概述开始，为读者铺就一条通往R语言网络分析专家之路。

# 2. 图论基础与R语言实现

图论是研究图的数学理论和方法，它是网络分析的数学基础。在社交网络分析中，图论的概念和工具被广泛应用于社交关系的建模与分析。R语言作为数据分析的利器，提供了强大的图论功能库，能够帮助我们更好地理解和操作图结构。

## 2.1 图论的基本概念

### 2.1.1 图的定义与分类

图（Graph）是由顶点（Vertex）集合和边（Edge）集合组成的抽象数据结构。在社交网络分析中，每个个体可以看作顶点，个体之间的关系可以看作边。

图可以被分为多种类型：

- **无向图**：边没有方向，如朋友关系。
- **有向图**：边有明确的方向，如关注关系。
- **加权图**：边有数值权重，如通信次数。
- **无权图**：边没有数值权重，即权重为1。

### 2.1.2 图的表示方法

图可以用多种方式表示：

- **邻接矩阵**：一个二维数组，其中元素表示顶点间的连接关系。
- **邻接表**：顶点列表，每个顶点关联一个边的列表。
- **边列表**：只包含边的信息，表示顶点间的连接。

### 2.1.3 图的R语言表示

在R中，我们可以用多种方式表示图。例如，使用`igraph`包，可以通过邻接矩阵或邻接列表来创建图对象。以下是一个简单的例子：

# 安装并加载igraph包
install.packages("igraph")
library(igraph)

# 创建一个无向图
edges <- matrix(c(1,2, 2,3, 3,1), ncol=2, byrow=TRUE)
g <- graph_from_edgelist(edges, directed=FALSE)

# 绘制图
plot(g)

## 2.2 图的结构特性分析

### 2.2.1 路径与连通性分析

路径（Path）是指顶点序列，序列中的每对顶点之间通过边相连。在分析社交网络时，路径可以帮助我们理解信息如何在网络中传播。

连通性分析则是研究图中节点是否通过路径相连。无向图的连通分量是指图中极大连通子图。有向图中，强连通分量（SCC）是最强形式的连通分量，图中任何两个顶点都是相互可达的。

### 2.2.2 中心性与子图分析

**中心性**指标帮助我们识别网络中的关键节点。常见的中心性指标有：

- **度中心性（Degree Centrality）**：节点的度数（与节点相连的边数）。
- **接近中心性（Closeness Centrality）**：节点到所有其他节点的平均距离。
- **中介中心性（Betweenness Centrality）**：节点在所有节点对最短路径上的出现频率。

子图（Subgraph）是从原图中提取出来的顶点和边的子集。分析子图可以帮助我们研究网络的局部结构特性。

## 2.3 使用R语言进行图的基本操作

### 2.3.1 构建图对象

在R中构建图对象是一个基本且重要的步骤。以下是创建不同图的示例：

# 创建无向图
g_undirected <- graph.formula(A-B, B-C, C-A)

# 创建有向图
g_directed <- graph.formula(A+-B, B+-C, C+-A)

# 创建加权图
g_weighted <- graph.formula(A-B(1), B-C(2), C-A(3))

# 使用邻接矩阵创建图
adj_matrix <- matrix(c(0,1,1,1,0,0,1,0,1), nrow=3, byrow=TRUE)
g_matrix <- graph_from_adjacency_matrix(adj_matrix, mode="undirected")

### 2.3.2 图的绘制与可视化

图的可视化对于理解网络结构非常有帮助。我们可以使用`igraph`包提供的`plot`函数来绘制图：

# 绘制无向图
plot(g_undirected, vertex.label=V(g_undirected)$name)

# 绘制有向图
plot(g_directed, vertex.label=V(g_directed)$name, edge.arrow.size=0.5)

# 使用布局来改善可视化效果
l <- layout.fruchterman.reingold(g_directed)
plot(g_directed, layout=l, vertex.label=V(g_directed)$name, edge.arrow.size=0.5)

接下来是第三章的内容。由于文章章节内容较多，为了保证连贯性和阅读体验，每个章节内容将独立编写，并遵循Markdown格式。请继续后续的章节内容。

### 第三章：社交网络分析理论与实践

社交网络分析涉及到对人类社交关系网络的研究，包括社交模式、群体结构、关键人物识别等多方面。在这一章节中，我们将深入了解社交网络分析的理论基础，并探讨如何使用R语言实践相关分析。

#### 3.1 社交网络的特点与分析方法

社交网络是由人与人之间的关系组成的复杂网络系统。社交网络的特点包括但不限于：

- **多边性**：多数情况下，社交关系是多边的，即多个个体可以同时与一个个体建立关系。
- **动态性**：社交关系不是静态的，它们随着时间推移而变化。
- **多样性**：社交关系的类型多样化，例如亲朋好友、工作同事、社交媒体关注等。

##### 3.1.1 社交网络的构成要素

社交网络由下列要素构成：

- **节点（Node）**：网络中的个体，可以是人、组织或其他实体。
- **边（Edge）**：代表节点之间的关系，可以是有向或无向的。
- **属性（Attribute）**：节点或边的附加信息，例如个体的年龄、性别、关系类型等。

##### 3.1.2 社交网络分析的理论框架

理论框架是分析社交网络的基础，它包含了：

- **网络密度**：衡量网络中实际边数与可能边数的比率。
- **聚类系数**：衡量网络中节点的聚集程度。
- **中心性分析**：确定网络中关键节点的方法，如度中心性、接近中心性、中介中心性等。

#### 3.2 社交网络数据的获取与预处理

##### 3.2.1 数据收集的途径

数据是进行社交网络分析的基础。数据收集的途径包括：

- **在线社交平台**：如Facebook、Twitter等，可以使用API抓取数据。
- **调查问卷**：直接通过问卷收集社交关系数据。
- **公共数据集**：如DBLP、IMDB等，这类数据集公开且易于获取。

##### 3.2.2 数据清洗与预处理技术

数据清洗与预处理包括以下步骤：

- **去重**：确保数据集中的数据没有重复项。
- **缺失值处理**：使用插值、删除或模型估计等方式处理缺失数据。
- **异常值检测与处理**：识别异常值，并进行适当处理以减少对分析的影响。

#### 3.3 社交网络的图表示与分析

##### 3.3.1 社交网络的图构建

在社交网络分析中，图构建涉及将收集到的数据转换为图模型。这包括：

- **节点映射**：将数据中的个体映射为图中的节点。
- **边映射**：将关系映射为图中的边。
- **属性映射**：将个体和关系的属性映射为图中节点和边的属性。

##### 3.3.2 社交网络的关键指标计算

社交网络分析中常用的关键指标包括：

- **度分布**：节点度数的分布情况。
- **连通性指标**：如连通分量的数量和大小。
- **子群结构**：网络中的群组或社区。

继续第四章内容。

### 第四章：社交网络分析进阶应用

社交网络分析的应用不仅局限于基础的网络结构分析，还可以深入到社区发现、网络动态行为分析以及影响力分析等进阶领域。这些高级分析可以帮助我们从更深层次理解社交网络的复杂性。

#### 4.1 社区发现与网络集群分析

社区发现是指在网络中识别出具有较强内部联系而与外部联系较弱的节点群。社区是社交网络分析中的一个核心概念，因为社区可以代表实际世界中的团体或群体，如兴趣小组、社交圈等。

##### 4.1.1 社区发现的算法原理

社区发现算法有多种形式，其中一些常用的算法包括：

- **层次聚类算法**：通过合并或分裂节点集合来形成社区。
- **模块度优化算法**：如Girvan-Newman算法，通过优化模块度来发现社区。

##### 4.1.2 网络集群的识别与分析

在识别出社区或集群之后，我们可以进一步分析其特征：

- **内部连通性**：社区内部节点的连通性分析。
- **外部连通性**：社区与社区之间的连通性分析。
- **关键节点识别**：社区内核心人物的识别。

#### 4.2 网络动态行为分析

社交网络是动态变化的，用户的互动、信息的传播都会引起网络结构的变化。

##### 4.2.1 网络的演化与动态模型

研究网络演化的动态模型可以帮助我们了解网络如何随时间变化：

- **增长模型**：如Barabási-Albert模型，通过特定规则生成网络。
- **优先附着模型**：节点根据特定优先级与已有节点建立连接。

##### 4.2.2 时间序列网络分析

时间序列网络分析是研究随时间变化的网络关系，例如：

- **时间窗口分析**：使用移动窗口来观察网络结构的短期变化。
- **时间戳边**：记录边存在的时间点，分析时间对网络的影响。

#### 4.3 社交网络的影响力分析

社交网络中的影响力是指某个节点对其他节点的影响能力。影响力分析是衡量个体影响力和影响力传播的重要方法。

##### 4.3.1 影响力的量化指标

影响力可以通过各种指标量化，包括：

- **接近中心性**：节点在社交网络中接近其他节点的程度。
- **PageRank**：一种算法，由Google创始人发明，用于排序网页。

##### 4.3.2 影响力传播模型与模拟

影响力传播模型可以帮助我们了解信息如何在网络中传播：

- **SIR模型**：用于模拟疾病传播的经典模型，可以类比应用于信息传播。
- **独立级模型（IC Model）**：每个被影响的节点有一定概率传播信息给它的邻居。

继续第五章内容。

### 第五章：R语言网络分析工具包介绍

R语言的网络分析工具包（或称为R包）是进行网络分析的利器，提供了丰富的方法和函数来简化分析过程。在这一章节中，我们将介绍一些常用的R包，并展示如何在实践中使用这些工具包来执行高级网络分析任务。

#### 5.1 常用的网络分析R包综述

##### 5.1.1 R包的安装与加载

安装和加载R包是使用R包的第一步。可以通过以下命令安装并加载`