常见的 JavaScript 数据结构与算法

# 1.1 数组的创建和初始化

在 JavaScript 中，可以使用两种主要方法创建数组：

1. **字面量语法：**使用方括号 `[]` 括起来的一组值，例如：

const myArray = [1, 2, 3, 4, 5];

2. **构造函数：**使用 `new Array()` 构造函数，后跟要创建的元素列表，例如：

const myArray = new Array(1, 2, 3, 4, 5);

数组可以存储各种类型的值，包括原始值（如数字、字符串、布尔值）和对象。数组的长度是动态的，可以根据需要添加或删除元素。

# 2. JavaScript 数组与链表

### 2.1 数组的特性和操作

#### 2.1.1 数组的创建和初始化

JavaScript 中的数组是一种有序的元素集合，每个元素都有一个索引。数组可以通过以下方式创建和初始化：

// 创建一个空数组
const arr = [];

// 创建一个包含元素的数组
const arr = [1, 2, 3, 4, 5];

// 使用数组字面量创建数组
const arr = [
  { name: "John", age: 30 },
  { name: "Jane", age: 25 },
];

#### 2.1.2 数组元素的访问和修改

数组元素可以通过其索引访问和修改。索引从 0 开始，表示数组中的第一个元素。

// 访问数组中的第一个元素
const firstElement = arr[0];

// 修改数组中的最后一个元素
arr[arr.length - 1] = 10;

### 2.2 链表的特性和操作

#### 2.2.1 链表的创建和初始化

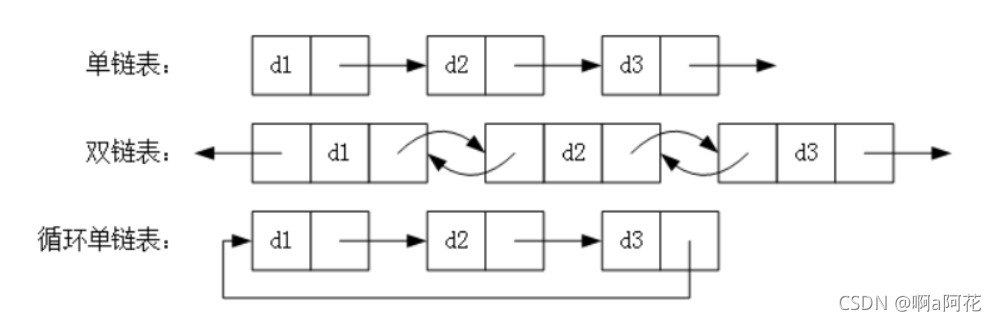
链表是一种线性数据结构，其中每个元素（称为节点）都包含一个值和指向下一个节点的指针。链表可以通过以下方式创建和初始化：

// 创建一个链表节点
const node = {
  value: 10,
  next: null,
};

// 创建一个链表
const head = node;

#### 2.2.2 链表元素的插入和删除

链表中的元素可以通过以下方式插入和删除：

// 在链表开头插入一个元素
head = {
  value: 20,
  next: head,
};

// 在链表末尾插入一个元素
let current = head;
while (current.next !== null) {
  current = current.next;
}
current.next = {
  value: 30,
  next: null,
};

// 删除链表中的一个元素
current = head;
while (current.next !== node) {
  current = current.next;
}
current.next = node.next;

# 3.1 栈的特性和操作

#### 3.1.1 栈的创建和初始化

栈是一种后进先出（LIFO）的数据结构，这意味着最后压入栈中的元素将首先弹出。在 JavaScript 中，可以使用数组来实现栈。

// 创建一个空栈
const stack = [];

#### 3.1.2 栈元素的压入和弹出

要将元素压入栈中，可以使用 `push()` 方法。要从栈中弹出元素，可以使用 `pop()` 方法。

// 压入元素
stack.push(1);
stack.push(2);
stack.push(3);

// 弹出元素
const poppedElement = stack.pop(); // 3

**代码逻辑逐行解读：**

* 第 2 行：将元素 1 压入栈中。
* 第 3 行：将元素 2 压入栈中。
* 第 4 行：将元素 3 压入栈中。
* 第 6 行：从栈中弹出元素，并将其存储在 `poppedElement` 变量中。弹出后，栈中只剩下元素 1 和 2。

**参数说明：**

* `push(element)`：将 `element` 压入栈中。
* `pop()`：从栈中弹出并返回栈顶元素。如果栈为空，则返回 `undefined`。

# 4. JavaScript 树与图

### 4.1 树的特性和操作

#### 4.1.1 树的创建和初始化

树是一种非线性数据结构，它由一个根节点和多个子节点组成，每个子节点又可以有多个子节点。树的创建可以通过以下步骤实现：

class Node {
  constructor(value) {
    this.value = value;
    this.children = [];
  }
}

class Tree {
  constructor() {
    this.root = null;
  }

  add(value) {
    if (!this.root) {
      this.root = new Node(value);
      return;
    }

    let current = this.root;
    while (current) {
      if (!current.children.length) {
        current.children.push(new Node(value));
        return;
      }
      current = current.children[0];
    }
  }
}

**代码逻辑分析：**

* `Node` 类表示树中的一个节点，它包含一个值和一个子节点数组。
* `Tree` 类表示一棵树，它包含一个根节点。
* `add` 方法用于向树中添加一个新节点。
* 如果树为空，则将新节点设为根节点。
* 否则，从根节点开始，一直遍历到最后一个子节点，然后将新节点添加到最后一个子节点的子节点数组中。

#### 4.1.2 树节点的遍历和搜索

树的遍历和搜索是常用的操作，可以通过以下方法实现：

// 深度优先遍历（DFS）
function dfs(node) {
  console.log(node.value);
  for (let child of node.children) {
    dfs(child);
  }
}

// 广度优先遍历（BFS）
function bfs(node) {
  let queue = [node];
  while (queue.length) {
    let current = queue.shift();
    console.log(current.value);
    for (let child of current.children) {
      queue.push(child);
    }
  }
}

// 搜索树中的节点
function search(tree, value) {
  let current = tree.root;
  while (current) {
    if (current.value === value) {
      return current;
    }
    current = current.children[0];
  }
  return null;
}

**代码逻辑分析：**

* `dfs` 函数使用深度优先遍历算法遍历树，从根节点开始，依次遍历每个子节点。
* `bfs` 函数使用广度优先遍历算法遍历树，从根节点开始，将所有子节点添加到一个队列中，然后依次从队列中取出节点进行遍历。
* `search` 函数使用深度优先遍历算法搜索树中的节点，从根节点开始，依次遍历每个子节点，直到找到目标节点。

### 4.2 图的特性和操作

#### 4.2.1 图的创建和初始化

图是一种非线性数据结构，它由一组顶点和连接这些顶点的边组成。图的创建可以通过以下步骤实现：

class Graph {
  constructor() {
    this.vertices = [];
    this.edges = [];
  }

  addVertex(vertex) {
    this.vertices.push(vertex);
  }

  addEdge(vertex1, vertex2) {
    this.edges.push([vertex1, vertex2]);
  }
}

**代码逻辑分析：**

* `Graph` 类表示一个图，它包含一个顶点数组和一个边数组。
* `addVertex` 方法用于向图中添加一个新顶点。
* `addEdge` 方法用于向图中添加一条新边，该边连接两个顶点。

#### 4.2.2 图的遍历和搜索

图的遍历和搜索是常用的操作，可以通过以下方法实现：

// 深度优先遍历（DFS）
function dfs(graph, start) {
  let visited = new Set();
  let stack = [start];
  while (stack.length) {
    let current = stack.pop();
    if (!visited.has(current)) {
      console.log(current);
      visited.add(current);
      for (let neighbor of graph.edges[current]) {
        if (!visited.has(neighbor)) {
          stack.push(neighbor);
        }
      }
    }
  }
}

// 广度优先遍历（BFS）
function bfs(graph, start) {
  let visited = new Set();
  let queue = [start];
  while (queue.length) {
    let current = queue.shift();
    if (!visited.has(current)) {
      console.log(current);
      visited.add(current);
      for (let neighbor of graph.edges[current]) {
        if (!visited.has(neighbor)) {
          queue.push(neighbor);
        }
      }
    }
  }
}

**代码逻辑分析：**

* `dfs` 函数使用深度优先遍历算法遍历图，从起始顶点开始，依次遍历每个相邻顶点。
* `bfs` 函数使用广度优先遍历算法遍历图，从起始顶点开始，将所有相邻顶点添加到一个队列中，然后依次从队列中取出顶点进行遍历。

# 5.1 排序算法

排序算法是计算机科学中用于对数据集合进行排序（按升序或降序排列）的算法。在 JavaScript 中，有许多不同的排序算法可供选择，每种算法都有其独特的特性和效率。

### 5.1.1 冒泡排序

冒泡排序是一种简单但效率较低的排序算法。它通过反复比较相邻元素并交换它们的位置来工作，直到列表中的所有元素按顺序排列。

**代码块：**

function bubbleSort(arr) {
  for (let i = 0; i < arr.length - 1; i++) {
    for (let j = 0; j < arr.length - 1 - i; j++) {
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }
  }
  return arr;
}

**逻辑分析：**

* 外层循环 `i` 表示当前正在比较的元素。
* 内层循环 `j` 表示与当前元素比较的相邻元素。
* 如果 `arr[j]` 大于 `arr[j + 1]`，则交换它们的顺序。
* 外层循环重复进行，直到列表中的所有元素按顺序排列。

**参数说明：**

* `arr`：要排序的数组。

### 5.1.2 快速排序

快速排序是一种高效的排序算法，它使用分治策略将列表划分为较小的子列表，然后递归地对子列表进行排序。

**代码块：**

function quickSort(arr) {
  if (arr.length <= 1) {
    return arr;
  }
  const pivot = arr[0];
  const left = [];
  const right = [];
  for (let i = 1; i < arr.length; i++) {
    if (arr[i] < pivot) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }
  return [...quickSort(left), pivot, ...quickSort(right)];
}

**逻辑分析：**

* 选择数组中的第一个元素作为枢轴点。
* 创建两个空数组 `left` 和 `right`，用于存储小于和大于枢轴点的元素。
* 遍历数组中的剩余元素，将它们分配到 `left` 或 `right` 数组中。
* 递归地对 `left` 和 `right` 数组进行排序。
* 将排序后的 `left` 数组、枢轴点和排序后的 `right` 数组合并为一个排序后的数组。

**参数说明：**

* `arr`：要排序的数组。

### 5.1.3 归并排序

归并排序是一种稳定的排序算法，它通过将列表拆分为较小的子列表，对子列表进行排序，然后合并排序后的子列表来工作。

**代码块：**

function mergeSort(arr) {
  if (arr.length <= 1) {
    return arr;
  }
  const mid = Math.floor(arr.length / 2);
  const left = mergeSort(arr.slice(0, mid));
  const right = mergeSort(arr.slice(mid));
  return merge(left, right);
}

function merge(left, right) {
  const merged = [];
  let leftIndex = 0;
  let rightIndex = 0;
  while (leftIndex < left.length && rightIndex < right.length) {
    if (left[leftIndex] < right[rightIndex]) {
      merged.push(left[leftIndex]);
      leftIndex++;
    } else {
      merged.push(right[rightIndex]);
      rightIndex++;
    }
  }
  return [...merged, ...left.slice(leftIndex), ...right.slice(rightIndex)];
}

**逻辑分析：**

* 将数组拆分为两个较小的子数组 `left` 和 `right`。
* 递归地对 `left` 和 `right` 子数组进行排序。
* 使用 `merge` 函数合并排序后的子数组。
* `merge` 函数通过比较 `left` 和 `right` 数组中的元素，将它们合并到一个排序后的数组中。

**参数说明：**

* `arr`：要排序的数组。

# 6. JavaScript 数据结构与算法的应用

### 6.1 数据结构在前端开发中的应用

#### 6.1.1 数组和链表用于数据存储和管理

* **数组：**用于存储同类型元素的集合，可通过索引快速访问和修改元素。
* **链表：**用于存储非连续元素的集合，每个元素包含数据和指向下一个元素的指针。

**应用场景：**

* 存储页面元素列表（数组）
* 实现下拉菜单（链表）
* 管理购物车中的商品（数组）

#### 6.1.2 栈和队列用于异步处理和消息传递

* **栈：**遵循后进先出（LIFO）原则，常用于函数调用和撤销操作。
* **队列：**遵循先进先出（FIFO）原则，常用于消息传递和事件处理。

**应用场景：**

* 管理浏览器历史记录（栈）
* 处理异步回调（队列）
* 实现消息队列（队列）

### 6.2 算法在后端开发中的应用

#### 6.2.1 排序算法用于数据排序和筛选

* **冒泡排序：**通过比较相邻元素并交换位置，将元素从小到大排序。
* **快速排序：**通过选择一个枢纽元素，将数组划分为两部分，然后递归排序每一部分。
* **归并排序：**将数组分成两部分，递归排序每一部分，然后合并两个排序好的部分。

**应用场景：**

* 对用户数据进行排序（冒泡排序）
* 查找特定数据（快速排序）
* 合并来自不同来源的数据（归并排序）

#### 6.2.2 搜索算法用于数据检索和优化

* **线性搜索：**从头到尾遍历数组，直到找到目标元素。
* **二分搜索：**将数组分成两部分，根据目标元素与中间元素比较，缩小搜索范围。

**应用场景：**

* 在大型数据集（二分搜索）中查找特定元素
* 优化数据库查询（线性搜索）
* 查找最佳匹配项（二分搜索）