【SVM模型迁移学习实战】：面向道路分割的创新应用


# 摘要
支持向量机（SVM）是一种有效的机器学习模型，广泛应用于模式识别、分类和回归分析。本文首先介绍了SVM的基础知识和理论，包括线性可分SVM、核技巧以及SVM的数学优化问题。随后，文章深入探讨了迁移学习在SVM中的应用，涵盖迁移学习的基本理论、SVM模型的迁移策略，以及在道路分割问题中的实践案例。文章还通过案例研究展示了SVM模型在道路分割数据集上的预处理、构建和优化，以及实验结果与分析。最后，本文展望了SVM模型迁移学习的未来，讨论了其在计算机视觉中的应用扩展、SVM模型的持续发展和挑战，以及道路分割技术的潜在进步和应用场景。

# 关键字
支持向量机；迁移学习；核技巧；数学优化；模型迁移；道路分割

参考资源链接：[SVM道路分割技术与资源分享](https://wenku.csdn.net/doc/7qyyxtj65d?spm=1055.2635.3001.10343)
# 1. 支持向量机（SVM）简介

支持向量机（SVM）是一种强大的机器学习算法，它在处理分类问题时表现出色，特别是在解决高维空间的数据分类任务中。其核心思想是找到一个最优的超平面，能够将不同类别的样本尽可能地分开，且间隔最大化。SVM不仅可以处理线性可分问题，还能通过核技巧解决非线性问题。由于其出色的泛化能力和稳健性，SVM广泛应用于模式识别、生物信息学和图像分析等多个领域。本章将对SVM进行基础介绍，并对其工作原理进行概述，为后续深入学习SVM的理论和应用打下坚实的基础。

# 2. SVM模型的理论基础

## 2.1 SVM的基本概念和原理

### 2.1.1 线性可分支持向量机

在机器学习领域，支持向量机（Support Vector Machine, SVM）是一种二分类模型，其基本模型定义为特征空间上间隔最大的线性分类器。线性可分支持向量机通过一个超平面将不同类别的数据样本分离，其基本假设是数据是线性可分的，即存在一条直线可以将两类数据完美分开。

在数学表达上，假设有一组线性可分的数据点 \( \{(x_i, y_i)\}_{i=1}^n \)，其中 \( x_i \) 是特征向量，\( y_i \in \{-1, 1\} \) 是类别标签。SVM 寻找一个超平面 \( w \cdot x + b = 0 \)，使得两类数据被该平面正确分割，并且最大化两类数据之间的间隔（margin）。间隔定义为离超平面最近的那些支持向量到平面的距离。

为了最大化间隔，我们需要解决以下优化问题：

\[ \text{minimize} \quad \frac{1}{2}||w||^2 \]

\[ \text{subject to} \quad y_i(w \cdot x_i + b) \geq 1, \quad i = 1, \dots, n \]

这里的 \( ||w|| \) 是权重向量的L2范数，它代表了超平面的正交距离。这个优化问题通过拉格朗日乘子法可以转化为其对偶问题来解决。

### 2.1.2 核技巧与非线性SVM

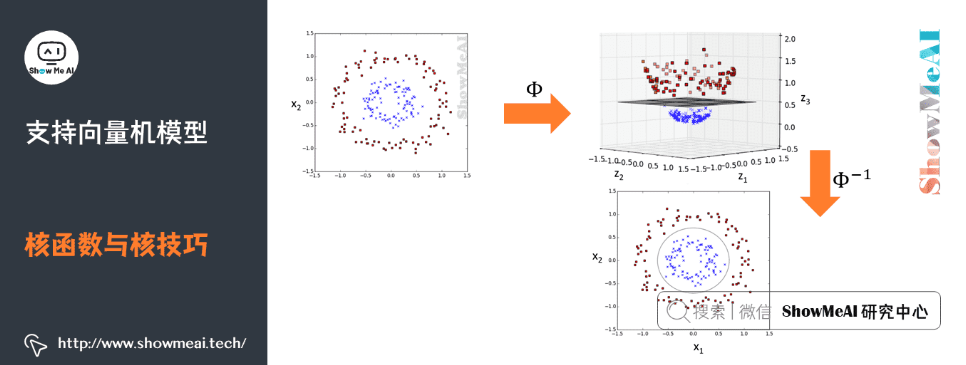
在实际应用中，并非所有数据都是线性可分的。核技巧（kernel trick）是SVM扩展到非线性分类的一种方法。核技巧的核心思想是通过一个非线性映射将原始数据映射到一个更高维的空间中，在这个新空间中，原本线性不可分的数据可能变得线性可分。

核函数定义为：

\[ K(x_i, x_j) = \Phi(x_i) \cdot \Phi(x_j) \]

其中，\( \Phi \) 是映射函数，\( K \) 是核函数。通过核函数，我们可以直接在原始特征空间中计算出新特征空间中的点积，从而避免直接计算高维空间的坐标，这样极大地简化了计算复杂度。

核技巧下的SVM模型称为非线性SVM，其优化问题变为：

\[ \text{minimize} \quad \frac{1}{2}||w||^2 \]

\[ \text{subject to} \quad y_i(K(x_i, x) + b) \geq 1, \quad i = 1, \dots, n \]

常用的核函数包括多项式核、高斯径向基函数（RBF）核和Sigmoid核等。

## 2.2 SVM模型的数学优化问题

### 2.2.1 拉格朗日乘子法

拉格朗日乘子法是一种寻找多元函数在一组约束下的极值的方法。SVM中的拉格朗日乘子法用来将原始的约束优化问题转化为无约束问题。

设原始问题为：

\[ \text{minimize} \quad f(x) \]

\[ \text{subject to} \quad g_i(x) \leq 0, \quad i = 1, \dots, m \]

\[ \quad \quad \quad h_j(x) = 0, \quad j = 1, \dots, p \]

拉格朗日函数（Lagrangian）定义为：

\[ L(x, \lambda, \alpha) = f(x) + \sum_{i=1}^{m} \lambda_i g_i(x) + \sum_{j=1}^{p} \alpha_j h_j(x) \]

其中，\( \lambda_i \geq 0 \) 和 \( \alpha_j \) 是拉格朗日乘子。根据KKT条件，一个点\( x^* \)是原始问题的解当且仅当存在一组乘子\( \lambda^* \) 和 \( \alpha^* \)，使得：

\[ \nabla_x L(x^*, \lambda^*, \alpha^*) = 0 \]

\[ \lambda_i^* g_i(x^*) = 0, \quad i = 1, \dots, m \]

\[ h_j(x^*) = 0, \quad j = 1, \dots, p \]

在SVM中，拉格朗日乘子法用于构造对偶问题，进而找到最优的权重向量 \( w \) 和偏置 \( b \)。

### 2.2.2 对偶问题与KKT条件

SVM的优化问题，无论是线性可分还是非线性问题，通过拉格朗日对偶性都可以转化为对偶问题。对偶问题的形式是通过拉格朗日函数的对偶来定义的，并且它只依赖于数据点之间的内积。对偶问题通常是更容易解决的二次规划问题。

对于SVM，其对偶问题可以表示为：

\[ \text{maximize} \quad \sum_{i=1}^{n} \alpha_i - \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j (x_i \cdot x_j) \]

\[ \text{subject to} \quad \alpha_i \geq 0, \quad i = 1, \dots, n \]

\[ \quad \quad \quad \sum_{i=1}^{n} \alpha_i y_i = 0 \]

在找到最优解 \( \alpha^* \) 后，可以通过它来计算原始问题中的权重向量 \( w \) 和偏置 \( b \)。Karush-Kuhn-Tucker（KKT）条件是优化问题的一个必要条件，特别是在凸优化问题中，它也是充分条件。

KKT条件包括：

1. 稳定性条件：\( \nabla_x L(x, \lambda, \alpha) = 0 \)
2. 原始可行性：\( g_i(x) \leq 0 \) 和 \( h_j(x) = 0 \)
3. 对偶可行性：\( \lambda_i \geq 0 \)
4. 互补松弛性：\( \lambda_i g_i(x) = 0 \)

满足KKT条件是SVM模型求解的关键。在SVM中，支持向量是那些对应非零拉格朗日乘子的样本点，它们直接参与决策边界的形成。

## 2.3 SVM模型的性能评估

### 2.3.1 交叉验证与模型选择

在机器学习中，模型选择和性能评估是至关重要的环节。交叉验证（cross-validation）是一种评估模型泛化能力的技术，通过使用训练集的不同子集重复训练和验证过程来减少模型评估中的方差。

最常用的交叉验证方法是K折交叉验证，它将训练数据集分成K个大小相等的子集，然后轮流将其中K-1个子集用作训练集，剩下1个用作验证集。这样可以得到K个模型性能的评估，最终将它们平均来估计模型泛化性能。

模型选择通常结合交叉验证，通过比较不同模型在交叉验证上的表现来选择最优模型。在SVM中，模型选择不仅包括选择合适的核函数，还包括调整核函数的参数（如RBF核的\( \gamma \)）以及SVM的正则化参数\( C \)。

### 2.3.2 模型泛化能力分析

模型泛化能力是指模型对未见过数据的预测能力。评估模型泛化能力的标准方法是使用测试集，它包含未在模型训练过程中使用的数据。

在SVM中，泛化能力可以