【异常检测：SVM在道路分割中的警觉眼】：识别非典型场景


# 摘要
本文系统地探讨了支持向量机（SVM）在道路分割和异常检测中的应用。首先介绍了SVM的理论基础及其在数据分类中的角色，重点分析了模型参数调优和性能评估指标。随后，详细阐述了道路分割的技术挑战以及异常检测的重要性，并展示了SVM在异常检测中的实践。通过案例研究，本文深入研究了SVM模型在道路异常检测中的实施过程，包括数据集准备、模型训练与测试，以及结果分析。最后，本文提出了SVM异常检测系统的开发思路，强调了系统设计、关键技术实现和后期维护的重要性，并对SVM技术的未来演进及道路异常检测的发展方向进行了展望。

# 关键字
支持向量机（SVM）；道路分割；异常检测；数据分类；模型优化；系统开发

参考资源链接：[SVM道路分割技术与资源分享](https://wenku.csdn.net/doc/7qyyxtj65d?spm=1055.2635.3001.10343)
# 1. SVM与道路分割概览

在本章中，我们将介绍SVM（支持向量机）的基础知识及其在道路分割任务中的重要性。SVM作为一种强大的机器学习模型，在数据分类、回归分析及异常检测等多个领域有着广泛的应用。道路分割作为计算机视觉领域的重要应用之一，旨在从道路上的图像数据中识别出路面区域，为交通监控、自动驾驶等技术提供关键数据支持。本章内容将为读者提供SVM和道路分割的基础知识框架，并为进一步深入学习各章节内容奠定基础。

## 1.1 SVM的基本原理

SVM通过找到数据集中支持向量的最佳位置，构建决策边界以最大化分类间隔。其核心在于找到一个超平面，将不同类别的数据有效地分开，其独特之处在于针对非线性问题，可以通过核函数将数据映射到更高维的空间中，从而提高模型的分类能力。

## 1.2 道路分割的挑战与SVM的应用

道路分割在自动驾驶和智能交通系统中至关重要，它需要从复杂的图像中准确识别出道路区域。SVM由于其良好的分类性能和优化灵活性，在道路分割中得到了广泛应用。但道路分割任务面临各种挑战，如天气变化、光线条件和复杂背景等，如何优化SVM以适应这些挑战是本章内容将要探讨的问题。

# 2. SVM理论基础与应用

## 2.1 SVM算法核心概念

### 2.1.1 SVM的定义与原理

支持向量机（Support Vector Machine，简称SVM）是一种基于统计学理论的监督学习方法，其核心思想在于构建一个超平面作为决策边界，将不同类别的数据分开。SVM特别擅长处理那些非线性可分的问题，这得益于其能够通过核技巧将数据映射到高维空间。在高维空间中，原本复杂的非线性问题可能变得线性可分。

SVM的原理可从线性可分情况开始理解。在二维空间中，寻找一个线性分类器等同于找到一条直线（在三维空间中是一平面，在更高维度上是一个超平面），这条直线可以最大限度地将两类数据点分开，而支持向量就是最靠近这条直线（超平面）的数据点。在实际操作中，SVM会尝试最大化分类间隔，即最接近的异类数据点与决策边界的距离。

逻辑分析：

graph TD
    A[开始] --> B[定义问题]
    B --> C[数据准备]
    C --> D[选择核函数]
    D --> E[训练模型]
    E --> F[评估模型]
    F --> G[应用模型]

参数说明：

- 在选择核函数时，常用的包括线性核、多项式核、径向基函数（RBF）核和Sigmoid核。
- 在模型训练阶段，通过求解一个优化问题找到最佳超平面。

### 2.1.2 支持向量与决策边界

在SVM模型中，支持向量是一组特殊的数据点，它们直接参与定义最优的决策边界。这些数据点位于分类超平面的边缘上，被称作“支持”超平面的“向量”。支持向量机的名称即来源于这些“支持向量”。

决策边界是由支持向量确定的最优超平面。如果数据是线性可分的，那么决策边界就是能够完美分割两类数据的直线或超平面。如果数据是非线性可分的，核技巧被用来将数据映射到更高维度的空间，以便在那个空间中数据变得线性可分。

在二分类问题中，模型的目标是最大化两个类别的间隔（即最小化间隔的倒数）。这个间隔定义为距离决策边界最近的任何数据点到边界的距离。找到这个最大间隔的边界，意味着构建了一个鲁棒的分类器，它具有良好的泛化能力。

代码块：

from sklearn.svm import SVC
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split

# 生成模拟数据集
X, y = make_blobs(n_samples=100, centers=2, random_state=6)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=6)

# 构建SVM分类器，默认使用RBF核
model = SVC(random_state=6)

# 训练模型
model.fit(X_train, y_train)

# 预测测试集结果
predictions = model.predict(X_test)

# 获取支持向量
support_vectors = model.support_vectors_

逻辑分析与参数说明：

- `make_blobs` 函数生成模拟数据集，`centers=2` 表示为二分类问题。
- 使用 `train_test_split` 将数据集分为训练集和测试集。
- `SVC` 是SVM的一种实现，其默认核函数是RBF核。
- 训练SVM模型后，可以调用 `support_vectors_` 属性来获取支持向量。

## 2.2 SVM在数据分类中的角色

### 2.2.1 分类任务与SVM

在机器学习的分类任务中，SVM扮演着核心角色之一。与其它分类算法相比，SVM在处理高维数据和非线性数据时表现出色。SVM能够有效处理小样本的数据分类问题，并且在引入核函数后，可以应对复杂的数据结构。这使得SVM在多个领域得到广泛的应用，包括图像识别、文本分类和生物信息学等。

SVM的另一个特点是它利用结构风险最小化原则，相比于经验风险最小化，更好地避免过拟合问题。此外，支持向量机通过最大化间隔来确保最优决策边界，这一特性使得SVM在处理异常值时也具有较强的鲁棒性。

### 2.2.2 核函数的作用与选择

核函数是SVM中用于处理非线性可分问题的关键组件。其核心思想是通过一个非线性映射函数将原始输入空间映射到一个更高维的特征空间，使得在这个新的空间里，原始数据能够变得线性可分。

核函数的选择依赖于数据的特性。对于线性可分的数据，可以直接使用线性核。对于非线性数据，常用的选择包括：

- 多项式核：能够处理非线性问题，可调整多项式的度数来控制模型复杂度。
- 径向基函数（RBF）核：也称高斯核，是处理非线性问题最常用的核函数，它只有一个参数（gamma），需要仔细调整以避免过拟合或欠拟合。
- Sigmoid核：与神经网络中的sigmoid函数有关，但在实践中使用较少。

在实际应用中，选择合适的核函数需要对数据进行充分的了解，并通过交叉验证等方法进行模型选择和参数优化。

## 2.3 SVM模型的优化与评估

### 2.3.1 模型参数调优

优化SVM模型是一个涉及多个参数的过程，主要包括核函数的选择和参数调整。通常，核函数参数（如RBF核的gamma和多项式核的degree）以及惩罚参数C都需要通过模型选择过程来调整。

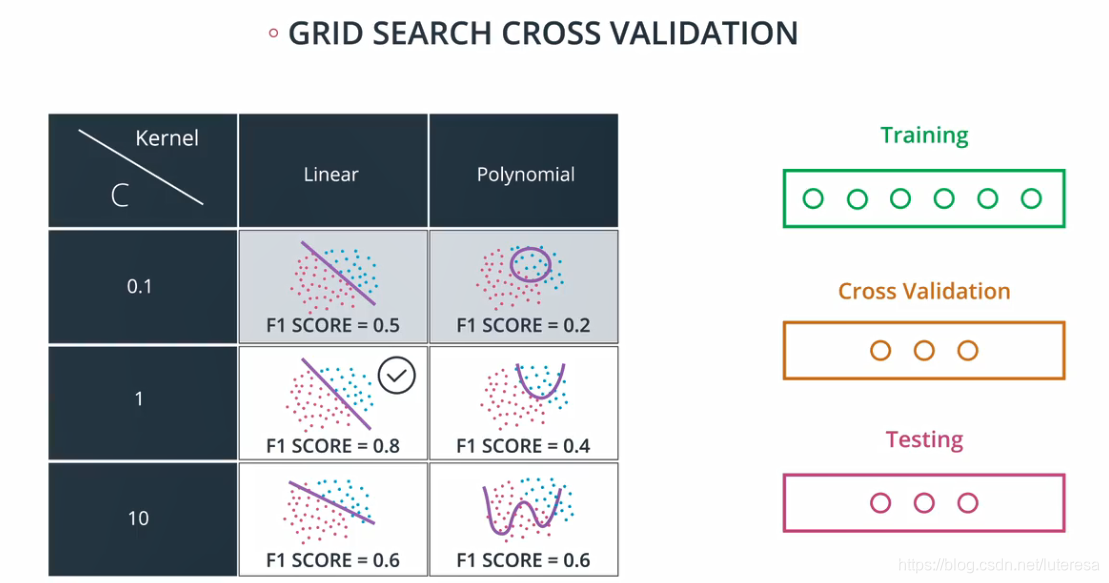
参数调整的方法通常有网格搜索（Grid Search）配合交叉验证。这种方法通过在预设的参数值范围内进行穷举搜索，找到最佳的参数组合。

代码块：

from sklearn.model_selection import GridSearchCV

# 设置SVM参数的范围
param_grid = {
    'C': [0.1, 1, 10, 100],
    'gamma': [1, 0.1, 0.01, 0.001],
    'kernel': ['rbf', 'poly']
}

# 创建SVM分类器
svc = SVC()

# 网格搜索模型
grid_search = GridSearchCV(svc, param_grid, cv=5)

# 拟合模型
grid_search.fit(X_train, y_trai