提升诊断和治疗的准确性：MATLAB数值积分在医学成像中的应用

# 1. MATLAB数值积分概述**

MATLAB数值积分是利用计算机技术对积分进行近似求解的方法。它通过将积分区间划分为多个子区间，并使用数值方法计算每个子区间的积分，从而得到整个积分的近似值。MATLAB中提供了多种数值积分函数，包括梯形法、辛普森法和高斯求积法。这些函数可以方便地用于求解各种积分问题。

数值积分在科学和工程领域有着广泛的应用，包括计算面积、体积、力矩和概率分布。在医学成像中，数值积分也发挥着至关重要的作用，例如在计算机断层扫描（CT）和磁共振成像（MRI）中用于图像重建。

# 2. MATLAB数值积分在医学成像中的理论基础

### 2.1 图像重建原理

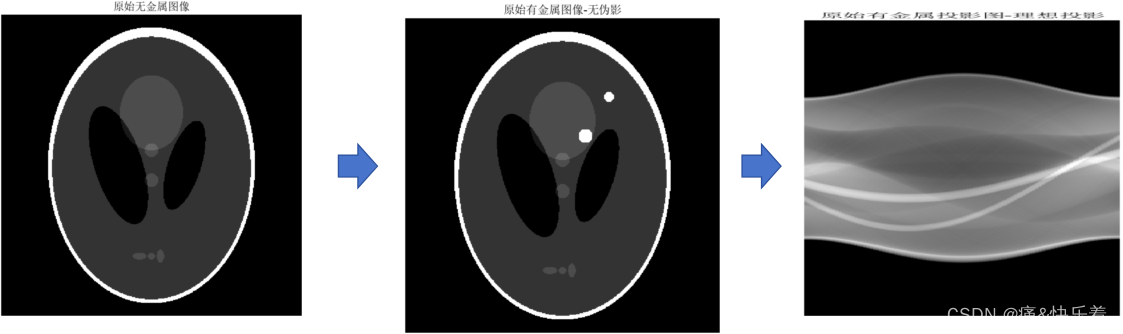
**2.1.1 投影定理**

投影定理是计算机断层扫描（CT）和磁共振成像（MRI）等医学成像技术的理论基础。它表明，物体沿某一方向的投影可以通过对物体内部沿该方向的线积分来获得。

**数学表达式：**

p(s, θ) = ∫∫f(x, y)δ(s - x cos θ - y sin θ) dx dy

* `p(s, θ)`：投影值
* `f(x, y)`：物体函数
* `δ`：狄拉克δ函数
* `s`：投影距离
* `θ`：投影角度

**2.1.2 反投影算法**

反投影算法是图像重建的基本技术，它通过将投影数据沿各个角度反向投影到图像空间来重建物体图像。

**数学表达式：**

f(x, y) = ∫p(s, θ)δ(x cos θ + y sin θ - s) ds dθ

### 2.2 数值积分在图像重建中的应用

**2.2.1 滤波反投影算法**

滤波反投影算法（FBP）是反投影算法的一种，它在反投影之前对投影数据进行滤波，以减少图像中的伪影。

**代码块：**

% 滤波反投影算法
[f, x, y] = filtered_backprojection(p, theta, filter);

% 参数说明：
% p: 投影数据
% theta: 投影角度
% filter: 滤波器

% 逻辑分析：
% 1. 对投影数据进行滤波
% 2. 对滤波后的投影数据进行反投影
% 3. 重建图像

**2.2.2 加权反投影算法**

加权反投影算法（WBP）是反投影算法的另一种，它通过对投影数据进行加权，以提高图像的质量。

**代码块：**

% 加权反投影算法
[f, x, y] = weighted_backprojection(p, theta, weights);

% 参数说明：
% p: 投影数据
% theta: 投影角度
% weights: 加权因子

% 逻辑分析：
% 1. 对投影数据进行加权
% 2. 对加权后的投影数据进行反投影
% 3. 重建图像

# 3. MATLAB数值积分在医学成像中的实践应用

### 3.1 CT成像

**3.1.1 数据采集和预处理**

CT（计算机断层扫描）成像是一种利用X射线穿透人体获取断层图像的医学成像技术。在CT成像中，X射线管绕着患者旋转，发射X射线束，而对面的探测器阵列接收穿透患者身体后的X射线。通过对接收到的X射线信号进行处理，可以获得患者身体内部的断层图像。

在CT成像中，MATLAB数值积分用于处理X射线投影数据，以重建患者身体内部的断层图像。具体来说，MATLAB数值积分可以用于执行以下任务：

* **滤波：**