低通滤波器在图像处理中的运用

# 1. 引言

在当今数字化时代，图像处理技术日益成熟，其在各个领域都有着广泛的应用。而滤波器作为图像处理中不可或缺的工具，扮演着至关重要的角色。通过对图像进行滤波处理，可以实现去噪、平滑、锐化等效果，从而提高图像质量和信息提取效率。数字信号处理作为图像处理的基础，涉及信号与系统的概念，傅里叶变换等重要知识点。滤波器的基础理论包括不同类型的滤波器分类和设计方法，如IIR与FIR滤波器。而数字图像处理基础则涉及数字图像表示与基本处理操作，为理解滤波器在图像处理中的应用提供了必要基础。在接下来的篇章中，我们将深入探讨低通滤波器在图像处理中的重要性及应用。

# 2. 数字信号处理基础

### 信号与系统概念

在数字信号处理中，信号代表了某种形式的数据，系统则对信号进行处理。时域分析关注信号随时间变化的特性，而频域分析则研究信号在频率域的特性。

离散信号由离散时刻的数值构成，连续信号则是在连续时间范围内的信号表示。

### 傅里叶变换

傅里叶变换是信号处理中的重要数学工具，能够将信号从时域转换到频域，揭示信号的频率特性。

连续傅里叶变换适用于连续信号，通过积分求解信号的频谱。离散傅里叶变换则用于离散信号，通过离散采样求解信号的频谱。

### 代码示例

import numpy as np

# 生成离散信号
signal = np.array([1, 2, 3, 4, 5])

# 进行离散傅里叶变换
transformed_signal = np.fft.fft(signal)

# 输出变换后的频谱
print(transformed_signal)

以上代码展示了对离散信号进行离散傅里叶变换的过程。

### 傅里叶变换流程图

graph LR
    A[时域信号] --> B(傅里叶变换)
    B --> C[频域信号]

在信号处理过程中，将信号从时域转换为频域，可以更清晰地理解信号的特性。

# 3. 滤波器基础理论

滤波器在数字信号处理中扮演着至关重要的角色，它可以帮助我们提取出信号中感兴趣的信息，抑制掉我们不需要的部分。本章将会对滤波器的基础理论进行介绍，包括滤波器的分类以及设计方法。

#### 滤波器分类

滤波器按照其频率响应特性可以被划分为不同类型，常见的包括低通滤波器、高通滤波器和带通滤波器。

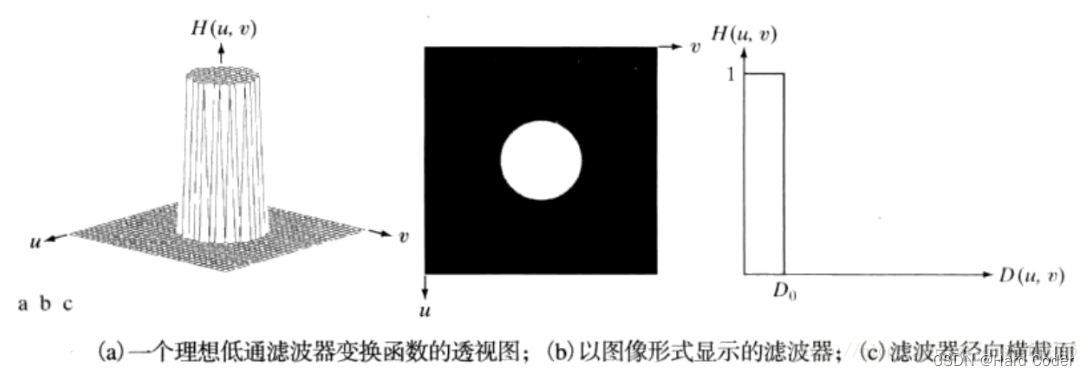
1. **低通滤波器**

低通滤波器允许低频信号通过并拒绝高频信号，常用于平滑信号或去除高频噪声。

2. **高通滤波器**

高通滤波器则允许高频信号通过，适用于去除低频信号或突出图像的边缘细节。

3. **带通滤波器**

带通滤波器能够选择性地通过一定频率范围内的信号，常用于特定频率范围内的信号处理。

#### 滤波器设计方法

根据滤波器的结构不同，其设计方法也会有所区别。常见的设计方法包括IIR滤波器和FIR滤波器。

##### IIR滤波器

IIR滤波器具有无限长的单位脉冲响应，常见的IIR滤波器包括巴特沃斯滤波器和切比雪夫滤波器。

- **巴特沃斯滤波器**：具有最平坦的幅度响应，适用于对幅度谱有严格要求的场景。
- **切比雪夫滤波器**：在通带或者阻带内可以实现更好的性能，但牺牲了幅度响应的平坦性。

##### FIR滤波器

FIR滤波器的单位脉冲响应是有限长的，常用的设计方法有窗函数法和频率采样法。

- **窗函数法设计**：通过选择合适的窗函数，可以实现不同的频率响应特性，如矩形窗、汉宁窗等。
- **频率采样法设计**：通过指定频率响应在若干点