低通滤波器在嵌入式系统设计中的关键作用

# 1. 嵌入式系统设计概述

在嵌入式系统设计中，理解基本概念至关重要。嵌入式系统是专为特定任务开发的计算机系统，通常被嵌入到其他设备中。应用领域广泛，涵盖消费电子、医疗设备、汽车电子等领域。设计嵌入式系统需要考虑资源受限、实时性要求高等特点，因此对硬件和软件的优化至关重要。通过合理的系统设计，可以实现功能强大的嵌入式系统，在不同领域发挥重要作用。随着技术的不断发展，嵌入式系统设计也在不断演进，更加注重性能和功耗的平衡，同时保证系统的稳定性和可靠性。深入了解嵌入式系统设计的基本概念和应用领域，对于工程师在实际项目中具有重要指导意义。

# 2. 信号处理在嵌入式系统中的重要性

在嵌入式系统中，信号处理扮演着至关重要的角色。通过对各种信号进行处理和分析，嵌入式系统能够实现各种功能，包括图像处理、音频处理、数据通信等。本章节将介绍信号处理在嵌入式系统中的基本原理以及不同信号处理算法的应用。

### 2.1 信号处理在嵌入式系统中的基本原理

在嵌入式系统中，信号处理是指对各种输入信号进行采集、处理和输出的过程。信号处理的基本原理包括信号采集、数字化、处理和输出。信号采集是指将模拟信号转换为数字信号，通常通过模数转换器（ADC）完成。数字化后的信号可以进行各种算法处理，如滤波、变换、编解码等。最后，处理后的信号经过数字模拟转换器（DAC）转换为模拟信号输出。

### 2.2 不同信号处理算法的应用

不同的信号处理算法在嵌入式系统中发挥着重要作用，其中最常见的包括傅立叶变换和数字滤波器。下面将分别介绍它们在嵌入式系统中的应用。

#### 2.2.1 傅立叶变换在嵌入式系统中的应用

傅立叶变换是将时域信号转换为频域信号的数学工具，可以用于频谱分析、滤波器设计等。在嵌入式系统中，傅立叶变换常用于实时信号处理，如音频频谱分析、图像处理等。

#### 2.2.2 数字滤波器的种类及特点

数字滤波器是一种对数字信号进行滤波处理的算法，常见的包括IIR滤波器和FIR滤波器。IIR滤波器具有递归特性，能够实现高阶滤波器；FIR滤波器则是非递归的，具有稳定性和线性相位特性。

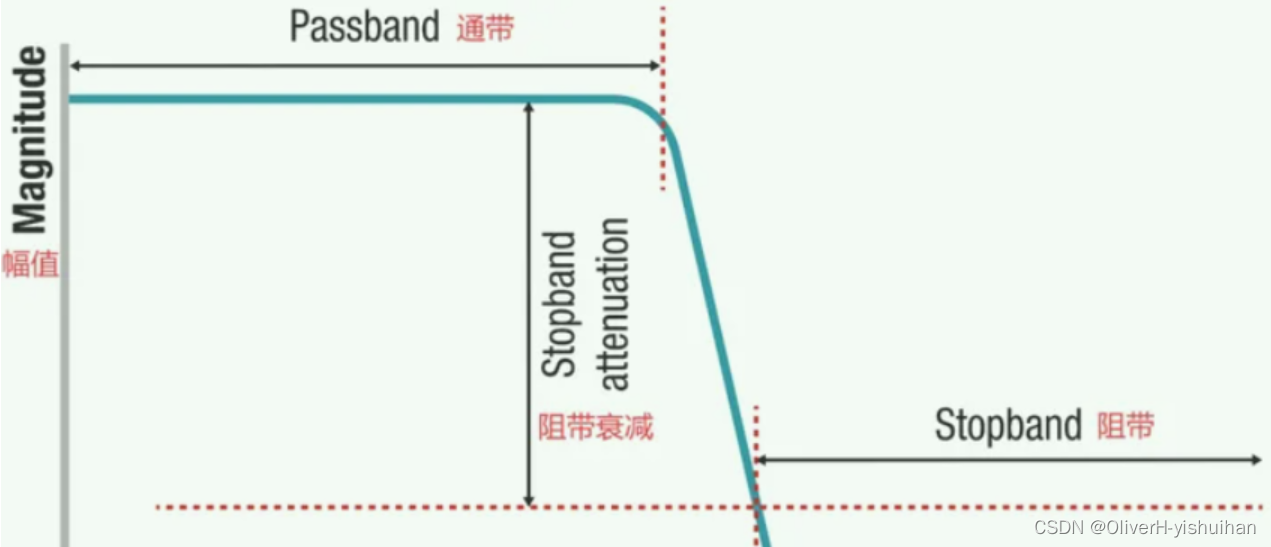
##### 2.2.2.1 低通滤波器的工作原理

低通滤波器是一种只允许低频信号通过的滤波器，常用于去除高频噪声或限制信号带宽。其工作原理是将高频信号衰减，而保留低频信号。

##### 2.2.2.2 高通滤波器的特点与适用场景

相对于低通滤波器，高通滤波器则是只允许高频信号通过的滤波器，常用于高频噪声的去除或高频信号的提取。其特点是将低频信号衰减，而保留高频信号。

# 3. 数字滤波器在嵌入式系统中的作用

#### 3.1 嵌入式系统中数字滤波器的作用及优势

数字滤波器在嵌入式系统中扮演着至关重要的角色。通过对信号进行滤波处理，数字滤波器可以去除噪声、平滑信号、提取特定频率成分等。在传感器数据处理、通信信号处理等方面，数字滤波器的应用尤为显著。与模拟滤波器相比，数字滤波器具有设计灵活、易于调整、数字化方便等优势。

#### 3.2 数字滤波器的分类和性能比较

##### 3.2.1 IIR滤波