单片机指令程序设计算法与数据结构：提升程序效率与性能

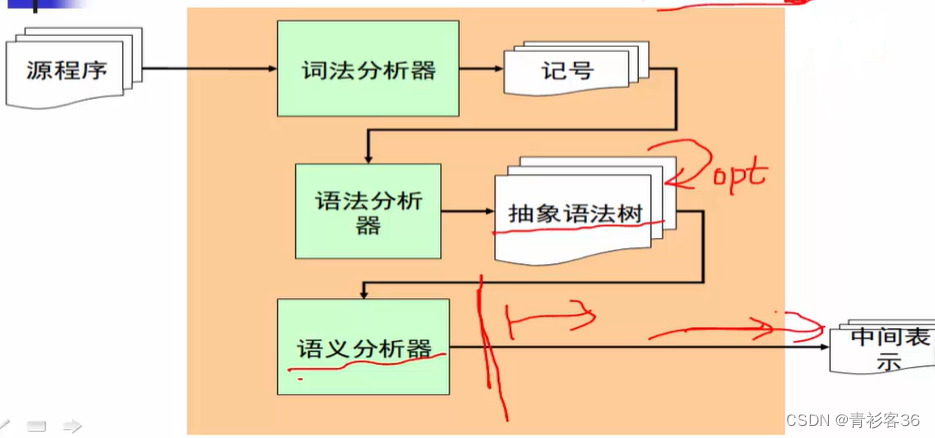
# 1. 单片机指令程序设计的理论基础

单片机指令程序设计是利用单片机指令集对单片机进行编程，实现特定功能的过程。其理论基础主要包括：

- **指令系统：**单片机指令集由一系列指令组成，每条指令对应特定的操作。
- **存储器结构：**单片机通常具有程序存储器和数据存储器，分别用于存储指令和数据。
- **处理器架构：**单片机处理器负责执行指令，其架构决定了指令执行的速度和效率。
- **汇编语言：**汇编语言是一种低级语言，直接操作单片机指令，可用于编写单片机程序。

# 2 单片机指令程序设计的算法优化

### 2.1 算法复杂度分析

#### 2.1.1 时间复杂度

时间复杂度是指算法执行时间与输入规模之间的关系，通常用大 O 符号表示。常见的复杂度类型包括：

- O(1)：常数时间复杂度，执行时间与输入规模无关。
- O(n)：线性时间复杂度，执行时间与输入规模 n 成正比。
- O(log n)：对数时间复杂度，执行时间与输入规模 n 的对数成正比。
- O(n^2)：平方时间复杂度，执行时间与输入规模 n 的平方成正比。
- O(2^n)：指数时间复杂度，执行时间随输入规模 n 的指数增长。

#### 2.1.2 空间复杂度

空间复杂度是指算法执行过程中占用的内存空间与输入规模之间的关系，也用大 O 符号表示。常见的复杂度类型包括：

- O(1)：常数空间复杂度，占用的内存空间与输入规模无关。
- O(n)：线性空间复杂度，占用的内存空间与输入规模 n 成正比。
- O(n^2)：平方空间复杂度，占用的内存空间与输入规模 n 的平方成正比。

### 2.2 算法设计策略

#### 2.2.1 分治法

分治法将问题分解成较小的子问题，分别解决子问题，然后将子问题的解合并得到原问题的解。

**代码块：**

void mergeSort(int arr[], int low, int high) {
    if (low < high) {
        int mid = (low + high) / 2;
        mergeSort(arr, low, mid);
        mergeSort(arr, mid + 1, high);
        merge(arr, low, mid, high);
    }
}

void merge(int arr[], int low, int mid, int high) {
    int i = low, j = mid + 1, k = 0;
    int temp[high - low + 1];
    while (i <= mid && j <= high) {
        if (arr[i] < arr[j]) {
            temp[k++] = arr[i++];
        } else {
            temp[k++] = arr[j++];
        }
    }
    while (i <= mid) {
        temp[k++] = arr[i++];
    }
    while (j <= high) {
        temp[k++] = arr[j++];
    }
    for (i = low; i <= high; i++) {
        arr[i] = temp[i - low];
    }
}

**逻辑分析：**

* `mergeSort` 函数将数组 `arr` 从 `low` 到 `high` 排序。
* 如果 `low` 小于 `high`，则将数组分为两个子数组，并递归调用 `mergeSort` 对子数组排序。
* `merge` 函数将两个已排序的子数组合并成一个已排序的数组。
* 两个指针 `i` 和 `j` 分别指向两个子数组的起始位置，指针 `k` 指向临时数组 `temp`。
* 比较两个子数组中的元素，将较小的元素添加到 `temp` 中。
* 最后，将 `temp` 中的元素复制回 `arr` 中。

#### 2.2.2 贪心法

贪心法在每一步中做出局部最优选择，希望最终得到全局最优解。

**代码块：**

int knapsack(int weights[], int values[], int capacity, int n) {
    int dp[n + 1][capacity + 1];
    for (int i = 0; i <= n; i++) {
        for (int j = 0; j <= capacity; j++) {
            if (i == 0 || j == 0) {
                dp[i][j] = 0;
            } else if (weights[i - 1] <= j) {
                dp[i][j] = max(values[i - 1] + dp[i - 1][j - weights[i - 1]], dp[i - 1][j]);
            } else {
                dp[i][j] = dp[i - 1][j];
            }
        }
    }
    return dp[n][capacity];
}

**逻辑分析：**

* `knapsack` 函数解决 0-1 背包问题，即给定物品的重量和价值，在容量为 `capacity` 的背包中装入物品，使得背包中的物品总价值最大。
* `dp` 数组记录了前 `i` 个物品装入容量为 `j` 的背包中的最大价值。
* 对于每个物品，如果其重量小于或等于背包的剩余容量，则可以选择装入背包，否则不装入。
* 最终，`dp[n][capacity]` 记录了所有物品装入容量为 `capacity` 的背包中的最大价值。

#### 2.2.3 动态规划

动态规划将问题分解成重叠子问题，先解决较小的子问题，然后逐步解决较大的子问题，最终得到原问题的解。

**代码块：**

int longestCommonSubsequence(char *str1, char *str2) {
    int m = strlen(str1);
    int n = strlen(str2);
    int dp[m + 1][n + 1];
    for (int i = 0; i <= m; i++) {
        dp[i][0] = 0;
    }
    for (int j = 0; j <= n; j++) {
        dp[0][j] = 0;
    }
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (str1[i - 1] == str2[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    return dp[m][n];
}

**逻辑分析：**

* `longestCommonSubsequence` 函数求两个字符串 `str1` 和 `str2` 的最长公共子序列的长度。
* `dp` 数组记录了 `str1` 的前 `i` 个字符和 `str2` 的前 `j` 个字符的最长公共子序列的长度。
* 如果 `str1[i - 1]` 和 `str2[j - 1]` 相等，则最长公共子序列的长度为 `dp[i - 1][j - 1]` 加 1。
* 否则，最长公共子序列的长度为 `dp[i - 1][j]` 和 `dp[i][j - 1]` 中的最大值。
* 最终，`dp[m][n]` 记录了 `str1` 和 `str2` 的最长公共子序列的长度。

# 3. 单片机指令程序设计的数据结构

### 3.1 数据结构基础

数据结构是组织和存储数据的方式，以便高效地访问和操作数据。在单片机指令程序设计中，选择合适的数据结构对于优化程序性能至关重要。

#### 3.1.1 线性表

线性表是一种数据结构，其中元素按顺序排列，每个元素只有一个前驱和一个后继。常见的线性表包括数组和链表。

- **数组**：数组是一种固定大小的数据结构，其中元素存储在连续的内存位置中。数组的优点是访问速度快，但缺点是大小不可变。
- **链表**：链表是一种动态数据结构，其中元素存储在不连续的内存位置中，每个元素包含数据和指向下一个元素的指针。链表的优点是大小可变，但缺点是访问速度较慢。

#### 3.1.2 栈和队列

栈和队列是两种特殊的线性表，具有特定的操作限制。

- **栈**：栈是一种后进先出（LIFO）数据结构，这意味着最后添加的元素将首先被删除。栈通常用于函数调用和递归。
- **队列**：队列是一种先进先出（FIFO）数据结构，这意味着最早添加的元素将首先被删除。队列通常用于消息传递和缓冲。

### 3.2 单片机指令程序设计中的数据结构应用

在单片机指令程序设计中，数据结构广泛用于组织和存储数据。

#### 3.2.1 数组和链表

数组和链表是单片机指令程序设计中常用的数据结构。

- **数组**：数组用于存储同类型的数据元素。数组的优点是访问速度快，但缺点是大小不可变。
- **链表**：链表用于存储可变长度的数据元素。链表的优点是大小可变，但缺点是访问速度较慢。

#### 3.2.2 树和图

树和图是更复杂的数据结构，用于组织和存储具有层次结构或关系的数据。

- **树**：树是一种层次结构的数据结构，其中每个节点最多有一个父节点和多个子节点。树用于表示文件系统、目录结构等。
- **图**：图是一种关系数据结构，其中节点表示对象，而边表示对象之间的关系。图用于表示社交网络、交通网络等。

### 代码示例

以下代码示例展示了在单片机指令程序设计中使用数组和链表：

; 定义一个数组
array: .byte 1, 2, 3, 4, 5

; 定义一个链表
node: .struct
    data: .byte
    next: .word
.endstruct

; 初始化链表
head: .word node
node: .struct
    data: .byte 1
    next: .word node2
.endstruct
node2: .struct
    data: .byte 2
    next: .word 0
.endstruct

### 逻辑分析

在上面的代码示例中，数组`array`是一个固定大小的数组，存储了五个字节的数据。链表`head`是一个指向链表第一个节点的指针。链表的每个节点包含一个字节的数据和一个指向下一个节点的指针。

# 4 单片机指令程序设计的实践应用

单片机指令程序设计在嵌入式系统、工业控制等领域有着广泛的应用。本章节将深入探讨单片机指令程序设计在这些领域的具体实践。

### 4.1 单片机指令程序设计在嵌入式系统中的应用

#### 4.1.1 传感器数据采集

嵌入式系统广泛应用于物联网、工业自动化等领域，需要采集各种传感器数据。单片机指令程序设计可以实现传感器数据的采集、处理和传输。

// 初始化ADC模块
ADC_InitTypeDef ADC_InitStruct;
ADC_InitStruct.ADC_Mode = ADC_Mode_Independent;
ADC_InitStruct.ADC_ScanConvMode = DISABLE;
ADC_InitStruct.ADC_ContinuousConvMode = ENABLE;
ADC_InitStruct.ADC_ExternalTrigConv = ADC_ExternalTrigConv_None;
ADC_InitStruct.ADC_DataAlign = ADC_DataAlign_Right;
ADC_InitStruct.ADC_NbrOfChannel = 1;
ADC_Init(ADC1, &ADC_InitStruct);

// 启动ADC转换
ADC_Cmd(ADC1, ENABLE);

// 等待转换完成
while (ADC_GetFlagStatus(ADC1, ADC_FLAG_EOC) == RESET);

// 读取转换结果
uint16_t adc_value = ADC_GetConversionValue(ADC1);

**逻辑分析：**

* 初始化ADC模块，设置转换模式、采样频率等参数。
* 启动ADC转换，并等待转换完成。
* 读取转换结果，并存储在变量`adc_value`中。

#### 4.1.2 实时控制

嵌入式系统还经常用于实时控制应用，如电机控制、温度控制等。单片机指令程序设计可以实现对实时系统的控制和管理。

// 初始化定时器
TIM_TimeBaseInitTypeDef TIM_TimeBaseInitStruct;
TIM_TimeBaseInitStruct.TIM_Period = 1000;
TIM_TimeBaseInitStruct.TIM_Prescaler = 7200;
TIM_TimeBaseInitStruct.TIM_ClockDivision = TIM_CKD_DIV1;
TIM_TimeBaseInitStruct.TIM_CounterMode = TIM_CounterMode_Up;
TIM_TimeBaseInit(TIM2, &TIM_TimeBaseInitStruct);

// 启动定时器
TIM_Cmd(TIM2, ENABLE);

// 定时器中断处理函数
void TIM2_IRQHandler(void)
{
    // 清除中断标志位
    TIM_ClearITPendingBit(TIM2, TIM_IT_Update);

    // 执行控制逻辑
    // ...
}

**逻辑分析：**

* 初始化定时器，设置定时周期、分频系数等参数。
* 启动定时器，并配置定时器中断。
* 在定时器中断处理函数中，执行控制逻辑，实现实时控制。

### 4.2 单片机指令程序设计在工业控制中的应用

#### 4.2.1 PLC编程

可编程逻辑控制器（PLC）广泛应用于工业自动化控制。单片机指令程序设计可以实现PLC程序的编写和调试。

// PLC程序示例
void PLC_Program(void)
{
    // 读取输入信号
    uint8_t input_signal = GPIO_ReadInputDataBit(GPIOA, GPIO_Pin_0);

    // 执行逻辑运算
    if (input_signal == 1)
    {
        // 输出信号
        GPIO_SetBits(GPIOB, GPIO_Pin_1);
    }
    else
    {
        // 清除输出信号
        GPIO_ResetBits(GPIOB, GPIO_Pin_1);
    }
}

**逻辑分析：**

* 读取输入信号，判断输入信号状态。
* 根据输入信号状态，执行逻辑运算，并输出控制信号。

#### 4.2.2 DCS系统

分布式控制系统（DCS）是工业自动化控制的高级系统。单片机指令程序设计可以实现DCS系统的通信、数据处理和控制。

// DCS通信协议解析示例
void DCS_ProtocolParse(uint8_t *data, uint16_t len)
{
    // 解析数据头
    uint8_t header = data[0];

    // 根据数据头，解析不同类型的数据
    switch (header)
    {
        case 0x01:
            // 解析数据类型1
            // ...
            break;
        case 0x02:
            // 解析数据类型2
            // ...
            break;
        default:
            // 解析失败
            // ...
            break;
    }
}

**逻辑分析：**

* 解析DCS通信协议的数据头，判断数据类型。
* 根据数据类型，解析不同格式的数据，并执行相应的处理逻辑。

# 5. 单片机指令程序设计的性能优化

### 5.1 代码优化

#### 5.1.1 指令优化

指令优化是指通过选择合适的指令和指令顺序来提高代码执行效率。以下是一些常用的指令优化技术：

- **使用高效指令：**选择执行效率更高的指令，例如使用单周期指令代替多周期指令。
- **指令流水线：**通过重排指令顺序，使指令能够重叠执行，提高指令吞吐量。
- **分支预测：**预测分支指令的跳转方向，提前加载目标指令，减少分支延迟。

#### 5.1.2 寄存器优化

寄存器优化是指通过有效利用寄存器来减少内存访问次数，提高代码执行速度。以下是一些寄存器优化技术：

- **变量分配：**将频繁使用的变量分配到寄存器中，减少内存访问。
- **寄存器溢出：**使用编译器优化选项，将溢出的寄存器变量存储到内存中，减少寄存器分配冲突。
- **寄存器重命名：**使用编译器优化选项，将寄存器变量重命名为更优化的名称，提高寄存器分配效率。

### 5.2 内存优化

#### 5.2.1 数据存储布局

数据存储布局是指将数据存储在内存中的方式。优化数据存储布局可以减少内存访问时间，提高代码执行效率。以下是一些数据存储布局优化技术：

- **数据对齐：**将数据对齐到其自然边界，减少内存访问次数。
- **局部变量放置：**将局部变量放置在栈中，而不是堆中，减少内存访问时间。
- **常量池：**将常量存储在常量池中，减少重复加载常量的内存访问。

#### 5.2.2 缓存优化

缓存优化是指通过有效利用缓存来减少内存访问时间，提高代码执行速度。以下是一些缓存优化技术：

- **数据局部性：**将经常一起使用的变量和指令存储在同一缓存行中，提高缓存命中率。
- **预取：**提前加载可能被访问的数据或指令，减少缓存未命中延迟。
- **缓存替换策略：**使用最优的缓存替换策略，替换最不经常使用的缓存行，提高缓存命中率。

# 6. 单片机指令程序设计的未来发展

随着单片机技术的不断发展，其指令集和程序设计工具也在不断进步，以满足日益增长的应用需求。

### 6.1 单片机指令集的扩展

为了满足不同应用场景的需求，单片机指令集也在不断扩展，主要体现在以下两个方面：

- **DSP指令集：**数字信号处理器（DSP）指令集专门用于处理数字信号，具有高效的乘法累加（MAC）和移位操作指令，可显著提高数字信号处理算法的执行效率。
- **浮点运算指令集：**浮点运算指令集支持浮点数据的运算，可以处理更复杂的数据类型，扩展了单片机的应用范围。

### 6.2 单片机指令程序设计工具的进步

为了提高单片机指令程序设计的效率和质量，单片机指令程序设计工具也在不断进步，主要体现在以下两个方面：

- **集成开发环境（IDE）：**IDE提供了一系列功能，包括代码编辑、编译、调试和仿真，可以帮助开发者快速开发和调试单片机程序。
- **调试和仿真工具：**调试和仿真工具可以帮助开发者实时跟踪程序执行，分析程序逻辑，查找和修复错误，提高程序开发效率。

随着单片机指令集的扩展和程序设计工具的进步，单片机指令程序设计将变得更加强大和高效，为嵌入式系统、工业控制等领域提供更强大的支持。