51单片机C语言程序设计中的PID控制与应用：精准调节的秘密

# 1. PID控制原理及算法**

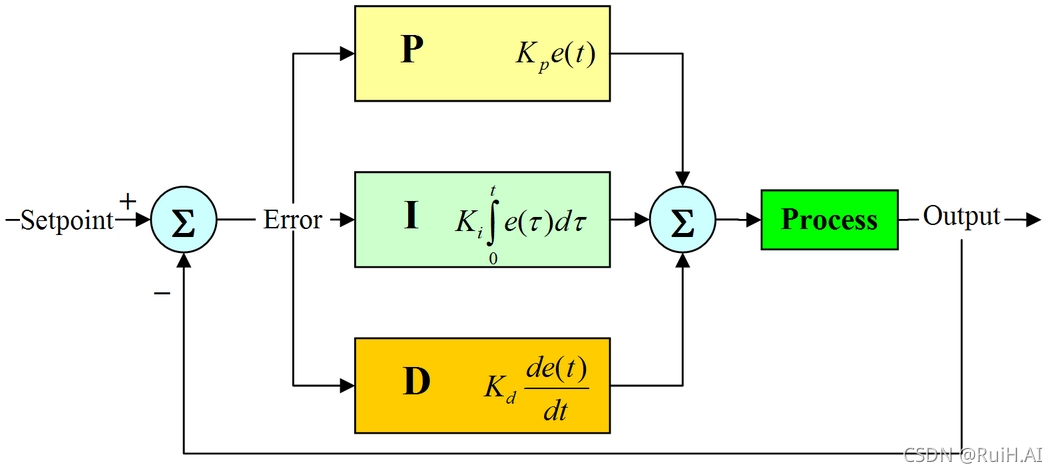
PID（比例-积分-微分）控制是一种经典的反馈控制算法，广泛应用于工业自动化、机器人控制等领域。其原理是通过测量系统输出与期望输出之间的误差，并根据误差的大小和变化率来调整控制器的输出，以达到控制目标。

PID算法由三个部分组成：比例项、积分项和微分项。比例项根据当前误差的大小进行调整，积分项根据误差的累积值进行调整，微分项根据误差的变化率进行调整。通过这三个部分的组合，PID控制器可以实现对系统输出的精确控制。

# 2. 51单片机C语言PID算法实现

### 2.1 算法流程及代码结构

PID算法的流程图如下：

graph LR
    A[采样] --> B[误差计算]
    B --> C[PID计算]
    C --> D[输出控制]

对应的C语言代码结构如下：

void PID_Control(float setpoint, float input) {
    // 采样与误差计算
    float error = setpoint - input;

    // PID计算
    float P = error * Kp;
    float I = error * Ki * dt;
    float D = (error - prev_error) / dt * Kd;

    // 输出控制
    float output = P + I + D;
}

### 2.2 变量定义及初始化

PID算法中需要定义和初始化以下变量：

| 变量 | 说明 |
|---|---|
| `setpoint` | 期望值 |
| `input` | 实际值 |
| `error` | 误差 |
| `Kp` | 比例系数 |
| `Ki` | 积分系数 |
| `Kd` | 微分系数 |
| `dt` | 采样周期 |
| `prev_error` | 上一次误差 |

### 2.3 采样与误差计算

采样是指获取实际值`input`，误差计算是指计算期望值`setpoint`与实际值`input`的差值。

float error = setpoint - input;

### 2.4 PID计算及输出控制

PID计算是指根据比例、积分、微分系数和误差计算PID输出。输出控制是指将PID输出转换为实际控制量。

float P = error * Kp;
float I = error * Ki * dt;
float D = (error - prev_error) / dt * Kd;

float output = P + I + D;

**参数说明：**

* `Kp`：比例系数，用于调整输出与误差的比例关系。
* `Ki`：积分系数，用于消除稳态误差。
* `Kd`：微分系数，用于预测误差变化趋势。
* `dt`：采样周期，用于计算积分和微分。
* `prev_error`：上一次误差，用于计算微分。

**逻辑分析：**

* 比例项`P`与误差成正比，误差越大，输出越大。
* 积分项`I`与误差的积分成正比，误差持续存在，输出将不断增大，直至消除误差。
* 微分项`D`与误差变化率成正比，误差变化越快，输出越大，有助于预测误差趋势，提高响应速度。

# 3. PID控制在51单片机应用实践

### 3.1 温度控制系统设计

#### 3.1.1 硬件电路设计

温度控制系统硬件电路主要包括传感器、放大器、单片机和执行器。

- 传感器：负责检测温度并将其转换为电信号。常用的温度传感器有热敏电阻、热电偶和红外传感器。
- 放大器：将传感器的弱信号放大到单片机可以识别的水平。
- 单片机：运行PID算法并控制执行器。
- 执行器：根据单片机的控制信号调节温度。常用的执行器有加热器、冷却器和风扇。

**硬件电路连接图：**

graph LR
subgraph 传感器
    A[热敏电阻] --> B[放大器]
end
subgraph 单片机
    C[单片机] --> D[执行器]
end
A --> C
D --> B

#### 3.1.2 PID参数整定

PID参数整定是根据系统特性确定PID算法中的比例、积分和微分系数。常用的整定方法有齐格勒-尼科尔斯法、科恩-科恩法和经验法。

**齐格勒-尼科尔斯法：**

1. 将PID算法的积分和微分系数设置为0。
2. 逐渐增加比例系数，直到系统出现持续振荡。
3. 记录振荡周期T。
4. 计算PID参数：
- 比例系数：Kp = 0.45 * T
- 积分时间：Ti = 0.85 * T
- 微分时间：Td = 0.12 * T

**科恩-科恩法：**

1. 将PID算法的积分和微分系数设置为0。
2. 逐渐增加比例系数，直到系统出现持续振荡。
3. 记录振荡周期T和振幅A。
4. 计算PID参数：
- 比例系数：Kp = 1.2 * A / T
- 积分时间：Ti = 2 * T