马尔可夫链揭秘：掌握随机过程中的Markov理论精髓


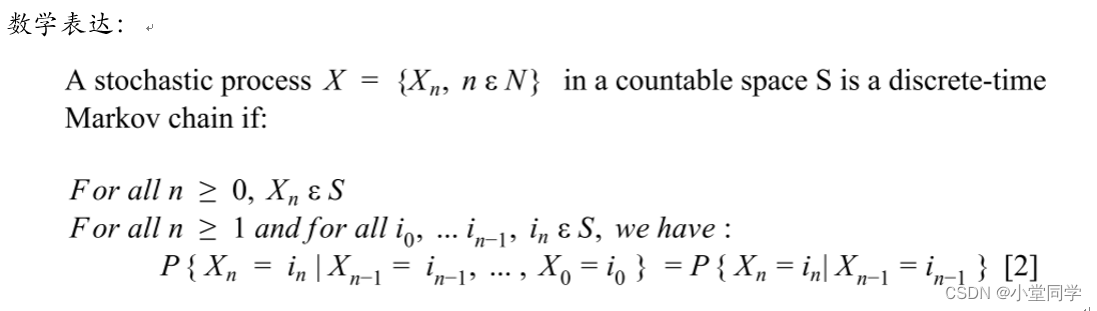
# 摘要
本文对马尔可夫链及其相关理论进行了全面的探讨，从基础概念到高级主题，涵盖了马尔可夫链的概率理论基础、计算方法与实际应用案例，以及马尔可夫决策过程与强化学习的结合。文章详细阐述了随机过程、马尔可夫链的定义、性质、分类、状态转移矩阵的计算、长期行为分析、高阶马尔可夫链、非齐次马尔可夫链和马尔可夫链蒙特卡洛（MCMC）方法。此外，还探讨了马尔可夫链在生物信息学、社交网络分析、经济预测、游戏AI开发和机器人导航控制等领域的应用。最后，通过编程实践章节，提供了一系列工具和库的使用指南以及模拟实现和案例分析，旨在帮助读者更好地理解和应用马尔可夫链。

# 关键字
马尔可夫链；随机过程；概率理论；强化学习；蒙特卡洛方法；编程实践

参考资源链接：[随机过程_STOCHASTIC_PROCESSES_(Second_Edition)_Sheldon_M._Ross](https://wenku.csdn.net/doc/6412b6f4be7fbd1778d48934?spm=1055.2635.3001.10343)
# 1. 马尔可夫链基础概述

马尔可夫链是一种数学模型，以俄国数学家安德烈·马尔可夫的名字命名。在这一章节中，我们将简要介绍马尔可夫链的基本概念，并概述其在现实世界中的应用。马尔可夫链主要用于描述一个系统的状态变化，其核心思想是系统的下一个状态仅依赖于当前状态，而与之前的状态无关，这被称为“无后效性”。

马尔可夫链在多个领域中均有广泛应用，例如经济学、生物学、物理学、计算机科学，甚至在语言学和音乐理论中也有出现。理解马尔可夫链的原理，可以帮助我们构建和分析系统行为的数学模型，预测未来的状态，并且优化决策过程。

我们将会看到，虽然马尔可夫链的概念听起来可能有些抽象，但其背后的数学逻辑是清晰且容易理解的。随着本文的深入，我们将逐步探索马尔可夫链的各个方面，从基础理论到计算方法，直至编程实践，最终能够熟练地在各个场景中应用这一强大的工具。

# 2. 马尔可夫链的概率理论基础

### 2.1 随机过程简介

随机过程是概率论中一个重要的研究对象，它描述了在某种随机试验中，由于随机性因素的影响，使得试验结果呈现动态变化的过程。随机过程的研究不仅涉及其在某一时刻的状态，还要考察其随时间发展的规律性。

#### 2.1.1 随机过程的定义和分类

随机过程可以定义为一个随机变量序列 {X(t), t ∈ T}，其中T是指标集（通常表示时间），对于任意的t∈T，X(t)表示在时间t的状态。这个序列中的每一个元素都是一个随机变量，它的取值可以是连续的也可以是离散的。

随机过程按照不同的标准可以分为多个类别。如果指标集T是离散的，那么相应的随机过程就称为离散时间随机过程；如果T是连续的，则称为连续时间随机过程。此外，随机过程还可以按照状态空间的性质分为离散型、连续型或混合型随机过程。

#### 2.1.2 随机过程的基本性质

在研究随机过程时，有几个重要的性质需要掌握，包括有限维分布、马尔可夫性质、平稳性和独立增量等。

- **有限维分布**描述了随机过程在任意有限个时间点上的联合分布。
- **马尔可夫性质**意味着过程未来的状态只依赖于当前状态，与过去的状态无关，这是一种无后效性的特征。
- **平稳性**指的是随机过程的统计特性不随时间的推移而改变。
- **独立增量**则是指未来状态的增量与过去状态的增量是相互独立的。

### 2.2 马尔可夫链的定义与性质

马尔可夫链是一种特殊的随机过程，它在每一步的状态转移只依赖于当前状态，而与之前的状态无关。这种性质使得马尔可夫链成为了建模复杂系统的有力工具。

#### 2.2.1 马尔可夫链的无后效性原理

无后效性原理是马尔可夫链的核心特征。数学上，对于离散时间马尔可夫链，该性质可以表示为：

P(X_{n+1} = j | X_n = i_n, X_{n-1} = i_{n-1}, ..., X_1 = i_1) = P(X_{n+1} = j | X_n = i_n)

对于任意的n, i_n, ..., i_1, j ∈ S（S是状态空间）。这意味着过程在时刻n+1的状态仅依赖于时刻n的状态。

#### 2.2.2 马尔可夫链的状态空间和转移概率

马尔可夫链的状态空间可以是离散的也可以是连续的。对于离散状态空间的马尔可夫链，转移概率可以通过状态转移矩阵P来描述：

P = [p_{ij}]_{i,j ∈ S}

其中，p_{ij} = P(X_{n+1} = j | X_n = i)，表示从状态i转移到状态j的概率。

### 2.3 马尔可夫链的分类

根据时间参数的不同，马尔可夫链可以分为离散时间马尔可夫链和连续时间马尔可夫链。

#### 2.3.1 离散时间马尔可夫链

离散时间马尔可夫链（DTMC）是最简单的马尔可夫链，其时间参数是离散的整数序列。状态转移在每个离散的时间点上进行。DTMC广泛应用于排队理论、存储理论、库存管理等领域。

#### 2.3.2 连续时间马尔可夫链

连续时间马尔可夫链（CTMC）的时间参数是连续的，并且转移发生的时间服从某种概率分布，如指数分布。CTMC在通信网络、生物化学反应、排队系统等领域的建模中有着不可替代的作用。

在下一章中，我们将探讨马尔可夫链的计算方法及其在不同领域的应用案例，深入理解马尔可夫链如何帮助我们解决实际问题。

graph TD;
    A[随机过程简介] --> B[随机过程的定义和分类];
    A --> C[随机过程的基本性质];
    B --> D1[离散时间随机过程];
    B --> D2[连续时间随机过程];
    C --> E1[有限维分布];
    C --> E2[马尔可夫性质];
    C --> E3[平稳性];
    C --> E4[独立增量];

    F[马尔可夫链的定义与性质] --> G[马尔可夫链的无后效性原理];
    F --> H[马尔可夫链的状态空间和转移概率];

    I[马尔可夫链的分类] --> J[离散时间马尔可夫链];
    I --> K[连续时间马尔可夫链];

通过上面的mermaid流程图，我们可以清晰地看到随机过程及其子主题之间的逻辑关系，以及马尔可夫链的定义、性质和分类之间的结构。

在本章节中，我们不仅介绍了随机过程的基本概念，还深入探讨了马尔可夫链的定义和性质，以及基于时间参数的分类。这些基础知识点为理解更高级的应用和计算方法提供了理论基础。接下来的章节将具体介绍马尔可夫链的计算方法，以及如何应用这些理论解决实际问题。

# 3. 马尔可夫链的计算方法与应用

马尔可夫链作为一种数学模型，在实际中有着广泛的应用，其计算方法是理解和应用马尔可夫链的核心。本章旨在深入探讨马尔可夫链的计算方法，并通过实际案例展示其在不同领域中的应用。

## 3.1 状态转移矩阵的计算

### 3.1.1 转移概率矩阵的构建

状态转移矩阵是马尔可夫链的核心元素，它描述了从一个状态到另一个状态的概率。构建转移概率矩阵是马尔可夫链计算的第一步。

以一个简单的天气预测模型为例，我们有三种可能的天气状态：晴天（Sunny）、多云（Cloudy）、下雨（Rainy）。假设根据历史数据，我们可以得到如下的转移概率矩阵：

flowchart LR
    A[Day1] -->|0.6| B[Day2]
    A -->|0.3| C[Day2]
    A -->|0.1| D[Day2]
    B -->|0.4| B
    B -->|0.4| C
    B -->|0.2| D
    C -->|0.3| B
    C -->|0.5| C
    C -->|0.2| D
    D -->|0.2| B
    D -->|0.5| C
    D -->|0.3| D

代码示例：

import numpy as np

# 定义一个3x3的状态转移矩阵
transition_matrix = np.array([
    [0.6, 0.3, 0.1],
    [0.4, 0.4, 0.2],
    [0.3, 0.5, 0.2]
])

print("状态转移矩阵:")
print(transition_matrix)

这里的 `transition_matrix` 就是描述天气状态转移的矩阵。每一行代表从当前状态转移到另一个状态的概率。

### 3.1.2 初始状态分布的确定

初始状态分布是指在起始时刻马尔可夫链可能处于的各个状态的概率分布。假设初始状态是随机的，我们可以给出一个初始状态分布。

代码示例：

# 定义初始状态分布
initial_distribution = np.array([0.5, 0.3, 0.2])

print("初始状态分布:")
print(initial_distribution)

`initial_distribution` 表示初始时刻，天气为晴天、多云、下雨的概率分别是 50%、30% 和 20%。

## 3.2 长期行为分析

### 3.2.1 吸收状态和周期状态

在马尔可夫链中，吸收状态是指一旦进入后就无法离开的状态，而周期状态则是指状态转移存在周期性循环。分析这些长期行为对于预测系统的未来行为至关重要。

#### 吸收状态

一个状态是吸收状态，如果从该状态出发的所有转移概率都是零，除了自身到自己的概率为1。

#### 周期状态

一个状态具有周期`d`（`d` > 1），如果从该状态出发，经过`d`步后再次返回该状态的概率为正，而经过任何小于`d`步数的概率为零。

代码示例：

# 计算达到吸收状态的概率（简化计算）
# 假设有一部分状态为吸收状态
absorbing_states = np.array([0, 0, 1])

# 计算到达吸收状态的概率矩阵
T = transition_matrix
I = np.identity