雷达系统波形设计与优化:提升性能的终极指南
发布时间: 2025-01-02 23:59:38 阅读量: 12 订阅数: 19 


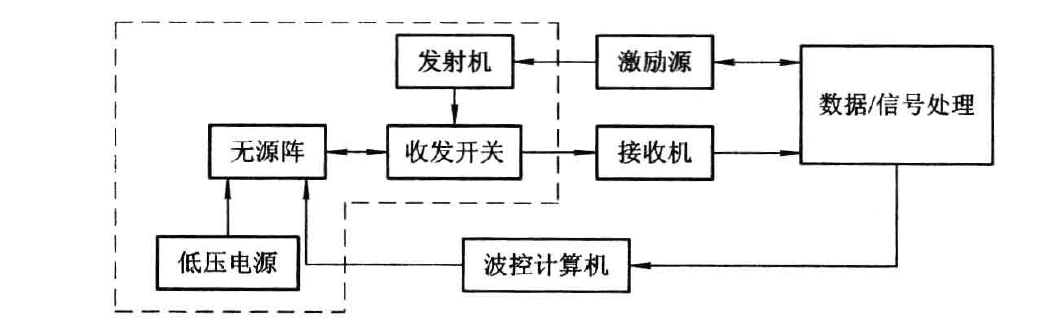
新体制雷达系统设计与优化问题研究
# 摘要
雷达系统波形设计是提高雷达性能和适应性的重要研究领域。本文首先概述了雷达波形设计的概念,继而深入探讨了波形设计的基础理论,包括信号处理、雷达信号特性和波形参数的影响。随后,本文详细介绍了波形设计的实践应用,包括在实际考量、常用设计方法以及波形优化技术方面。此外,文章还讨论了波形优化策略与算法,特别是传统优化方法、现代技术以及机器学习方法在波形设计中的应用。实验与案例分析章节通过实践验证了优化策略的效果。最后,本文展望了雷达波形设计的未来发展趋势和挑战,强调了波形设计对雷达系统整体性能的长期影响,并提出了对后续研究的建议。
# 关键字
雷达系统;波形设计;信号处理;优化算法;机器学习;实验分析
参考资源链接:[雷达系统导论 Introduction to Radar Systems Third Edition (Merrill I. Skolnik)](https://wenku.csdn.net/doc/6465c2d65928463033d05639?spm=1055.2635.3001.10343)
# 1. 雷达系统波形设计概述
在现代雷达系统中,波形设计是实现高效探测和目标识别的关键技术之一。本章将为您提供波形设计的简介、重要性以及在雷达系统中的核心作用。
## 1.1 波形设计的定义和目的
波形设计本质上涉及信号的时域和频域特性选择,以满足特定的雷达探测要求。其目的在于优化雷达系统的性能,提高目标检测精度,增强抗干扰能力,并在一定的功率和带宽约束下,最大化雷达的作用距离和分辨率。
## 1.2 波形设计在雷达系统中的作用
波形设计在雷达系统中扮演着至关重要的角色。一个精心设计的波形可以使得雷达在复杂电磁环境下仍能有效地探测目标,同时对目标进行精准的定位和测量。此外,波形的设计还会影响到系统的隐蔽性,即在不被敌方察觉的情况下获取信息的能力。
在本章中,我们将回顾波形设计的基本概念,并为后续章节中对波形设计基础理论和实践应用的深入探讨打下坚实的基础。
# 2. 波形设计的基础理论
### 2.1 信号处理基础
在雷达系统中,信号处理是核心组成部分,它涉及到信号的产生、接收、处理以及解释。理解和运用信号处理的基础知识,对于设计高效的雷达波形至关重要。
#### 2.1.1 信号的时域与频域表示
信号可以通过其在时域(时间轴)的表现来分析,也可以通过频域(频率轴)来理解。时域分析侧重于信号的时间特性,比如信号的持续时间、周期性等。频域分析侧重于信号中各个频率成分的分布情况。
在时域,脉冲信号可以表示为具有一定持续时间和幅度的函数。例如,理想的矩形脉冲信号可以用一个矩形函数来表示:
```math
rect(t) = \begin{cases}
1 & \text{for } |t| < \frac{T}{2} \\
0 & \text{otherwise}
\end{cases}
```
其中,T是脉冲的宽度。
频域表示则是将信号转换为不同频率的正弦波之和。傅里叶变换是信号从时域到频域转换的基本工具。经过傅里叶变换后,信号的频谱可揭示其频率成分,这对于设计雷达波形以匹配特定传输特性至关重要。
#### 2.1.2 傅里叶变换及其在信号分析中的应用
傅里叶变换(Fourier Transform)可以将时域信号转换为频域信号。快速傅里叶变换(Fast Fourier Transform, FFT)是一种高效实现傅里叶变换的算法,广泛用于数字信号处理中。
频域中的信号分析对于波形设计有以下作用:
- **频带分析**:确定信号所占用的频带宽度,有助于设计合适的波形以避免频谱干扰。
- **信号滤波**:通过分析频谱,可以设计滤波器来过滤特定频率成分。
- **信号调制与解调**:对于调制信号,频域分析有助于设计更好的调制解调策略。
一个简化的FFT代码实现示例如下:
```python
import numpy as np
def fft(signal):
N = len(signal)
if N <= 1: return signal
even = fft(signal[0::2])
odd = fft(signal[1::2])
T = [np.exp(-2j * np.pi * k / N) * odd[k] for k in range(N // 2)]
return [even[k] + T[k] for k in range(N // 2)] + [even[k] - T[k] for k in range(N // 2)]
# 示例信号
signal = np.array([1, 0, 0, 0, 0, 0, 0, 1])
# 执行FFT变换
fft_signal = fft(signal)
# 输出频域信号的幅度
fft_magnitude = [abs(x) for x in fft_signal]
```
通过上述代码,我们得到了信号在频域的表示,即信号的频谱。频谱的幅度部分可以告诉我们信号在哪些频率成分上更加强烈,这在波形设计中是一个关键信息。
### 2.2 雷达信号的特性
雷达波形设计不仅需要理解信号的一般特性,还需要深入认识特定于雷达信号的特性。这包括脉冲调制信号和编码信号等。
#### 2.2.1 脉冲调制信号的种类和特性
脉冲调制信号是雷达系统中最常用的信号形式之一。它通过改变脉冲的某些特性(如幅度、宽度、位置等)来传递信息。
脉冲调制信号可以分为以下几种:
- **脉冲幅度调制(PAM)**:通过改变脉冲的幅度来携带信息。
- **脉冲宽度调制(PWM)**:通过改变脉冲的宽度来携带信息。
- **脉冲位置调制(PPM)**:通过改变脉冲在周期中的位置来携带信息。
每种调制方式都具有不同的优缺点,并且对波形设计有不同的要求。例如,PAM信号在传输时容易受到噪声的影响,而PPM信号则对同步精度要求较高。
#### 2.2.2 相位编码信号和频率编码信号分析
相位编码信号和频率编码信号是两种更复杂的调制技术,它们通过改变信号的相位或频率来携带信息。
- **相位编码信号**(如Barker码)通过改变发射信号的相位来实现编码。相位编码的优点是可以提高信号的隐蔽性和抗干扰能力,但也增加了接收端的处理复杂性。
- **频率编码信号**(如频率调制连续波FM-CW)通过改变信号的频率来实现编码,它适合于连续波雷达系统,可以提供距离和速度的联合测量。
### 2.3 波形参数的影响
波形参数是波形设计的重要方面,它们对雷达系统的性能有着显著的影响。熟悉这些参数的作用可以帮助设计者更精确地控制雷达的行为。
#### 2.3.1 脉冲宽度和重复频率的作用
脉冲宽度和重复频率是脉冲雷达系统中的关键参数。
- **脉冲宽度(Pulse Width, PW)**:决定了雷达的分辨率以及距离测量的精度。较窄的脉冲宽度可以提供更高的距离分辨率。
- **重复频率(Pulse Repetition Frequency, PRF)**:影响了雷达的最大可测距离和盲速。较高的PRF允许雷达测量更远的距离,但也可能导致信号重叠,造成盲速。
#### 2.3.2 频率带宽和峰值功率的关系
频率带宽和峰值功率是决定雷达信号检测性能的两个重要参数。
- **频率带宽(Bandwidth, BW)**:带宽越宽,信号的频率分辨率越高,可以提供更高的距离分辨率,但同时也会增加系统的复杂性。
- **峰值功率**:较高的峰值功率可以增加雷达的检测距离,但同样会增加系统的复杂性和成本。
通过调整这些参数,可以设计出适应不同应用场景的雷达波形。例如,在设计用于远程监测的雷达时,可能更倾向于增加峰值功率以提高检测距离;而在设计用于城市交通监控的雷达时,则可能会考虑减少带宽以降低干扰。
在实际设计过程中,波形参数的选择和优化是一个综合考量多个系统需求和约束的过程。设计者必须权衡不同参数对系统性能的影响,并进行必要的折衷。
## 第三章:波形设计的实践应用
### 3.1 波形设计中的实际考量
在波形设计的实践中,除了理论上的知识外,还需考虑到许多实际因素,这些因素包括雷达方程、检测性能以及抗干扰能力等。
#### 3.1.1 雷达方程与检测性能
雷达方程是描述雷达探测距离与信号功率之间关系的基本方程。它将雷达的发射功率、天线增益、目标截面积、接收机灵敏度等因素联系起来。波形设计需要考虑如何最大化这些参数,以提升雷达的检测性能。
雷达方程一般表达式为:
```math
P_r = \frac{{P_t G_t G_r \lambda^2 \sigma}}{{(4\pi)^3 R^4 L}}
```
其中,\(P_r\) 是接收到的功率,\(P_t\) 是发射功率,\(G_t\) 和 \(G_r\) 分别是发射和接收天线增益,\(\lambda\) 是信号波长,\(\sigma\) 是目标的有效反射面积,\(R\) 是目标距离,\(L\) 是系统损耗。
利用该方程,设计师可以优化波形参数,比如增加发射功率或提高天线增益,以提高雷达的探测距离和灵敏度。
#### 3.1.2 抗干扰能力与隐蔽性要求
在现代电子战环境中,雷达系统不仅需要具备良好的检测性能,还要有较强的抗干扰能力以及隐蔽性。为了达到这些要求,波形设计时需要考虑如下因素:
- **频谱控制**:合理分配和控制频谱资源,避免与其他系统信号的冲突。
- **信号编码**:使用先进的编码技术,如扩频技术,来增加信号的隐蔽性和抗干扰能力。
- **信号调制**:选择适宜的调制方式,如相位调制和频率调制,可以提高波形的抗干扰性能。
抗干扰波形设计的一个关键点是利用信号的冗余,通过引入伪随机码或特
0
0






