揭秘单片机控制马达的算法秘籍：轻松解决控制难题

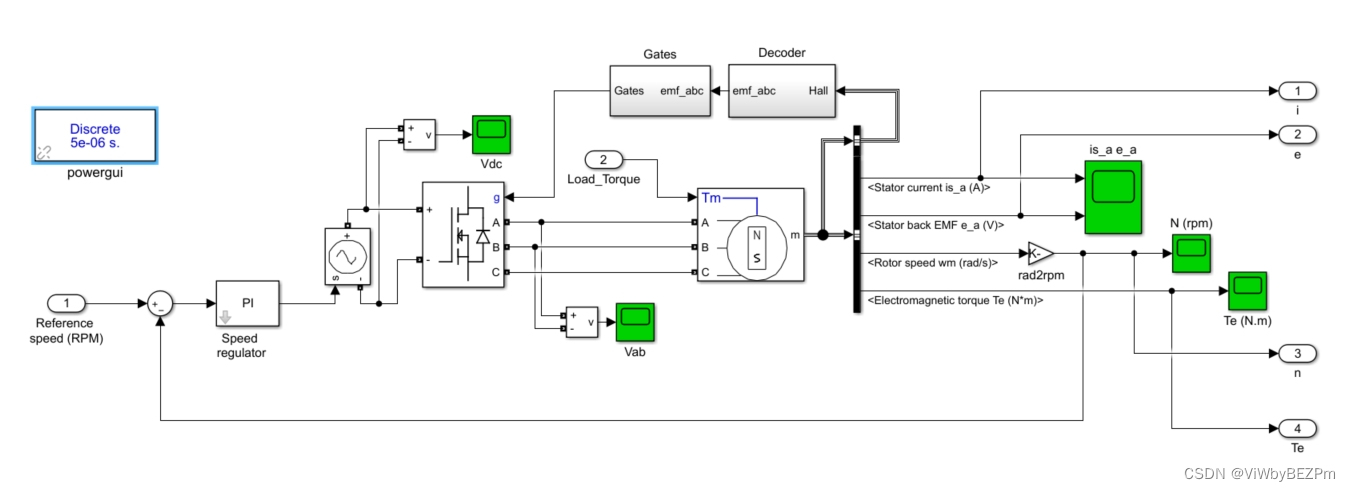
# 1. 单片机控制马达概述**

单片机控制马达是一种常见的工业应用，它利用单片机控制马达的转速、位置和方向。单片机是一种微型计算机，具有处理数据和控制外设的能力。通过使用单片机，可以实现对马达的精确控制，提高系统的效率和可靠性。

单片机控制马达的原理是通过控制马达的驱动电路，进而改变马达的转速、位置和方向。常见的马达驱动电路包括H桥电路、全桥电路和PWM电路。单片机通过输出不同的控制信号，可以控制驱动电路的开关状态，从而控制马达的运行。

# 2. 单片机控制马达的理论基础

### 2.1 电机驱动原理

**直流电机**

直流电机是一种将电能转换为机械能的旋转电机。其工作原理基于电磁感应定律，即当电流流过导体时，会在导体周围产生磁场。当导体置于磁场中时，会受到电磁力的作用，从而产生旋转运动。

**交流电机**

交流电机是一种将交流电能转换为机械能的旋转电机。其工作原理基于电磁感应定律和电磁感应定律的逆定律。当交流电通过定子绕组时，会在定子中产生旋转磁场。旋转磁场与转子导条相互作用，产生感应电流，从而产生电磁力并驱动转子旋转。

### 2.2 单片机控制电机的方式

**脉宽调制（PWM）**

PWM是一种通过控制脉冲的宽度来调节输出电压或电流的技术。在单片机控制电机中，PWM用于控制电机驱动器的输出电压，从而实现对电机速度和方向的控制。

**H桥驱动**

H桥驱动是一种使用四个开关（两个高侧开关和两个低侧开关）来控制电机方向和速度的电路。通过控制开关的开闭，可以实现电机正转、反转和制动。

#### 代码块示例：

# PWM控制电机速度
import time
import RPi.GPIO as GPIO

# 设置GPIO引脚
pwm_pin = 18
GPIO.setmode(GPIO.BCM)
GPIO.setup(pwm_pin, GPIO.OUT)

# 设置PWM频率和占空比
pwm = GPIO.PWM(pwm_pin, 100)  # 频率为100Hz
pwm.start(50)  # 占空比为50%

# 运行电机
time.sleep(5)

# 停止电机
pwm.stop()
GPIO.cleanup()

**逻辑分析：**

* 该代码使用RPi.GPIO库控制树莓派上的GPIO引脚。
* 将GPIO引脚18设置为PWM输出引脚。
* 设置PWM频率为100Hz，占空比为50%。
* 启动PWM输出，电机开始旋转。
* 5秒后，停止PWM输出，电机停止旋转。
* GPIO.cleanup()释放引脚资源。

#### 表格示例：

| PWM参数 | 说明 |
|---|---|
| 频率 | PWM输出信号的频率 |
| 占空比 | PWM输出信号中高电平所占的比例 |
| 分辨率 | PWM输出信号中最小可调的占空比 |

#### Mermaid流程图示例：

sequenceDiagram
participant Motor
participant Single-chip microcomputer
Motor->Single-chip microcomputer: Request control
Single-chip microcomputer->Motor: Send PWM signal
Motor->Single-chip microcomputer: Update status

**逻辑分析：**

* 流程图描述了单片机控制电机的一般流程。
* 单片机通过发送PWM信号来控制电机。
* 电机接收PWM信号并更新其状态。
* 单片机根据电机的状态调整PWM信号，实现对电机的控制。

# 3.1 PID控制算法

#### 3.1.1 PID算法原理

PID（比例-积分-微分）控制算法是一种经典的反馈控制算法，广泛应用于各种控制系统中。其基本原理是通过测量被控对象的输出值与期望值之间的偏差，并根据偏差的大小和变化率，计算出控制量，从而调整被控对象的输入值，使输出值接近期望值。

PID算法的数学表达式如下：

u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt

其中：

* `u(t)` 为控制量
* `e(t)` 为偏差，即期望值与输出值之差
* `Kp` 为比例增益
* `Ki` 为积分增益
* `Kd` 为微分增益

**比例控制**：比例控制项 `Kp * e(t)` 与偏差成正比，当偏差较大时，控制量也较大，从而快速减小偏差。

**积分控制**：积分控制项 `Ki * ∫e(t)dt` 与偏差的累积值成正比，当偏差持续存在时，控制量会逐渐增大，从而消除偏差的稳态误差。

**微分控制**：微分控制项 `Kd * de(t)/dt` 与偏差的变化率成正比，当偏差变化较快时，控制量也会快速变化，从而抑制偏差的过冲和振荡。

#### 3.1.2 PID算法参数整定

PID算法的性能与参数 `Kp`、`Ki` 和 `Kd` 的设置密切相关。参数整定方法有多种，常见的有：

* **经验法**：根据经验和试错来调整参数，直到系统达到满意的性能。
* **齐格勒-尼科尔斯法**：一种基于系统阶跃响应的自动整定方法。
* **遗传算法**：一种基于进化论思想的优化算法，可以自动搜索最优参数。

参数整定的目标是找到一组参数，使系统具有以下性能：

* **快速响应**：系统对偏差的反应速度快，偏差迅速减小。
* **稳定性**：系统不会出现持续的振荡或不稳定现象。
* **鲁棒性**：系统对参数变化和外部干扰具有较强的抵抗能力。

# 4. 单片机控制马达的实践应用

### 4.1 电机速度控制

#### 4.1.1 PID控制电机速度

**原理：**

PID控制是一种经典的反馈控制算法，通过测量电机实际速度与目标速度之间的误差，并根据误差的比例（P）、积分（I）和微分（D）项来计算控制量，从而调整电机速度。

**代码实现：**

import time

# PID参数
Kp = 0.1
Ki = 0.01
Kd = 0.001

# 目标速度
target_speed = 100

# 实际速度
actual_speed = 0

# 误差
error = target_speed - actual_speed

# 积分误差
integral_error = 0

# 微分误差
derivative_error = 0

# 控制量
control_value = 0

while True:
    # 更新实际速度
    actual_speed = get_motor_speed()

    # 计算误差
    error = target_speed - actual_speed

    # 计算积分误差
    integral_error += error * time.dt

    # 计算微分误差
    derivative_error = (error - previous_error) / time.dt

    # 计算控制量
    control_value = Kp * error + Ki * integral_error + Kd * derivative_error

    # 更新控制量
    set_motor_control_value(control_value)

    # 更新误差
    previous_error = error

    # 延时
    time.sleep(time.dt)

**逻辑分析：**

* `get_motor_speed()`函数获取电机的实际速度。
* `set_motor_control_value()`函数根据控制量调整电机速度。
* `time.dt`为控制周期。
* PID参数`Kp`、`Ki`和`Kd`根据电机特性进行整定。
* 误差、积分误差和微分误差用于计算控制量。
* 控制量通过`set_motor_control_value()`函数更新电机速度。

#### 4.1.2 模糊控制电机速度

**原理：**

模糊控制是一种基于人类经验和知识的控制算法，它将电机速度和控制量映射到模糊集合中，并根据模糊规则推导出控制量。

**代码实现：**

# 模糊集合
motor_speed = {"slow": [0, 50], "medium": [50, 100], "fast": [100, 150]}
control_value = {"low": [0, 50], "medium": [50, 100], "high": [100, 150]}

# 模糊规则
rules = [
    ("slow", "low"),
    ("slow", "medium"),
    ("medium", "medium"),
    ("medium", "high"),
    ("fast", "high")
]

# 目标速度
target_speed = 100

# 实际速度
actual_speed = 0

while True:
    # 更新实际速度
    actual_speed = get_motor_speed()

    # 模糊化
    motor_speed_level = fuzzify(actual_speed, motor_speed)
    target_speed_level = fuzzify(target_speed, motor_speed)

    # 推理
    control_value_level = infer(motor_speed_level, target_speed_level, rules)

    # 反模糊化
    control_value = defuzzify(control_value_level, control_value)

    # 更新控制量
    set_motor_control_value(control_value)

    # 延时
    time.sleep(time.dt)

**逻辑分析：**

* `fuzzify()`函数将实际速度和目标速度模糊化为模糊集合。
* `infer()`函数根据模糊规则推导出控制量的模糊集合。
* `defuzzify()`函数将控制量的模糊集合反模糊化为具体值。
* 模糊规则根据电机特性和控制要求制定。
* 控制量通过`set_motor_control_value()`函数更新电机速度。

### 4.2 电机位置控制

#### 4.2.1 PID控制电机位置

**原理：**

PID控制电机位置与速度控制类似，但误差为电机实际位置与目标位置之间的差值。

**代码实现：**

# PID参数
Kp = 0.1
Ki = 0.01
Kd = 0.001

# 目标位置
target_position = 100

# 实际位置
actual_position = 0

# 误差
error = target_position - actual_position

# 积分误差
integral_error = 0

# 微分误差
derivative_error = 0

# 控制量
control_value = 0

while True:
    # 更新实际位置
    actual_position = get_motor_position()

    # 计算误差
    error = target_position - actual_position

    # 计算积分误差
    integral_error += error * time.dt

    # 计算微分误差
    derivative_error = (error - previous_error) / time.dt

    # 计算控制量
    control_value = Kp * error + Ki * integral_error + Kd * derivative_error

    # 更新控制量
    set_motor_control_value(control_value)

    # 更新误差
    previous_error = error

    # 延时
    time.sleep(time.dt)

**逻辑分析：**

* `get_motor_position()`函数获取电机的实际位置。
* `set_motor_control_value()`函数根据控制量调整电机位置。
* PID参数`Kp`、`Ki`和`Kd`根据电机特性进行整定。
* 误差、积分误差和微分误差用于计算控制量。
* 控制量通过`set_motor_control_value()`函数更新电机位置。

#### 4.2.2 模糊控制电机位置

**原理：**

模糊控制电机位置与速度控制类似，但误差为电机实际位置与目标位置之间的差值。

**代码实现：**

# 模糊集合
motor_position = {"left": [0, 50], "center": [50, 100], "right": [100, 150]}
control_value = {"low": [0, 50], "medium": [50, 100], "high": [100, 150]}

# 模糊规则
rules = [
    ("left", "low"),
    ("left", "medium"),
    ("center", "medium"),
    ("center", "high"),
    ("right", "high")
]

# 目标位置
target_position = 100

# 实际位置
actual_position = 0

while True:
    # 更新实际位置
    actual_position = get_motor_position()

    # 模糊化
    motor_position_level = fuzzify(actual_position, motor_position)
    target_position_level = fuzzify(target_position, motor_position)

    # 推理
    control_value_level = infer(motor_position_level, target_position_level, rules)

    # 反模糊化
    control_value = defuzzify(control_value_level, control_value)

    # 更新控制量
    set_motor_control_value(control_value)

    # 延时
    time.sleep(time.dt)

**逻辑分析：**

* `fuzzify()`函数将实际位置和目标位置模糊化为模糊集合。
* `infer()`函数根据模糊规则推导出控制量的模糊集合。
* `defuzzify()`函数将控制量的模糊集合反模糊化为具体值。
* 模糊规则根据电机特性和控制要求制定。
* 控制量通过`set_motor_control_value()`函数更新电机位置。

# 5. 单片机控制马达的优化技术

在单片机控制马达的实际应用中，为了提高控制精度、稳定性和响应速度，需要对算法和硬件进行优化。

### 5.1 算法优化

#### 5.1.1 PID参数优化

PID控制算法的控制效果受PID参数（比例系数、积分系数、微分系数）的影响。优化PID参数可以提高控制精度和稳定性。

**优化方法：**

* ** Ziegler-Nichols 方法：**一种经典的PID参数整定方法，基于阶跃响应曲线。
* **遗传算法：**一种基于进化论的优化算法，通过迭代搜索最优参数。
* **粒子群算法：**一种基于鸟群行为的优化算法，通过群体协作寻找最优参数。

#### 5.1.2 模糊规则优化

模糊控制算法的控制效果受模糊规则的影响。优化模糊规则可以提高控制精度和鲁棒性。

**优化方法：**

* **专家知识：**根据专家经验制定模糊规则。
* **遗传算法：**通过迭代搜索最优模糊规则。
* **强化学习：**一种基于奖励和惩罚的学习算法，通过试错学习最优模糊规则。

### 5.2 硬件优化

#### 5.2.1 电机驱动电路优化

电机驱动电路的性能直接影响电机的控制效果。优化电机驱动电路可以提高控制精度和效率。

**优化方法：**

* **选择合适的驱动器：**根据电机类型和控制要求选择合适的驱动器。
* **优化驱动器参数：**调整驱动器参数（如电流、电压、频率）以优化电机性能。
* **采用隔离措施：**隔离电机驱动电路和单片机，防止干扰。

#### 5.2.2 单片机选型优化

单片机的性能和资源影响控制算法的执行效率。优化单片机选型可以提高控制速度和响应时间。

**优化方法：**

* **选择合适的单片机：**根据控制算法的复杂度和实时性要求选择合适的单片机。
* **优化单片机配置：**调整单片机时钟频率、内存分配等配置以优化性能。
* **采用并行处理：**利用多核单片机或外部协处理器进行并行处理，提高计算效率。

通过对算法和硬件的优化，可以有效提高单片机控制马达的性能，满足不同应用场景的控制要求。

# 6. 单片机控制马达的应用案例

单片机控制马达技术广泛应用于工业、家居、医疗等领域，以下列举几个典型案例：

### 6.1 工业机器人

**应用场景：**
工业机器人中，单片机负责控制机器人的电机，实现机器人的运动和操作。

**技术方案：**
- 采用高性能单片机，如 ARM Cortex-M 系列，具有强大的计算能力和实时性。
- 使用 PID 或模糊控制算法，精确控制机器人的运动轨迹和速度。
- 通过 CAN 总线或 EtherCAT 等工业通信协议，与上位控制系统通信。

### 6.2 智能家居

**应用场景：**
智能家居中，单片机控制马达实现电器设备的自动化控制，如窗帘、空调、扫地机器人等。

**技术方案：**
- 采用低功耗单片机，如 STM32L 系列，满足智能家居设备的低功耗要求。
- 使用简单易用的控制算法，如开环控制或闭环控制，实现设备的开关、调速等功能。
- 通过 Wi-Fi、蓝牙或 Zigbee 等无线通信技术，与智能家居网关或手机 APP 通信。

### 6.3 医疗器械

**应用场景：**
医疗器械中，单片机控制马达实现医疗设备的精准控制，如手术机器人、呼吸机、输液泵等。

**技术方案：**
- 采用高可靠性单片机，如 TI MSP430 系列，满足医疗器械的安全性和稳定性要求。
- 使用先进的控制算法，如自适应控制或鲁棒控制，保证医疗器械的精度和可靠性。
- 通过 RS-232、USB 或以太网等通信接口，与上位监控系统或医疗设备连接。