MATLAB数据分析中的统计建模：回归分析和时间序列分析，揭示数据背后的规律

# 1. MATLAB数据分析概述**

MATLAB是一种强大的技术计算语言，广泛用于数据分析、建模和可视化。它提供了丰富的函数和工具箱，使数据科学家和工程师能够高效地处理和分析大型数据集。

MATLAB数据分析涉及使用统计建模技术从数据中提取有意义的见解。这些技术包括回归分析、时间序列分析和机器学习算法。通过这些技术，数据分析人员可以探索数据模式、预测未来趋势并做出明智的决策。

MATLAB在数据分析中的优势在于其易用性和灵活性。它提供了一个交互式环境，使用户能够快速探索数据、开发模型并可视化结果。此外，MATLAB与其他编程语言和软件（如Python、R和SQL）的集成，使数据分析人员能够根据需要扩展其分析功能。

# 2.1 概率论与数理统计

### 2.1.1 概率分布与统计量

**概率分布**描述了随机变量可能取值的分布情况。常见概率分布包括：

- **正态分布：**钟形曲线，用于描述连续随机变量。
- **二项分布：**用于描述重复独立实验中成功次数的分布。
- **泊松分布：**用于描述一段时间内发生的事件数的分布。

**统计量**是描述样本数据特征的数值，例如：

- **均值：**样本数据的平均值。
- **方差：**样本数据离散程度的度量。
- **标准差：**方差的平方根，表示样本数据分布的离散程度。

### 2.1.2 抽样与假设检验

**抽样**是从总体中随机抽取一部分数据，以推断总体特征。

**假设检验**是一种统计推断方法，用于检验假设是否成立。假设检验过程包括：

1. **提出假设：**提出关于总体参数的假设。
2. **收集数据：**从总体中抽取样本。
3. **计算检验统计量：**使用样本数据计算一个统计量，用于检验假设。
4. **确定临界值：**根据假设和样本量确定一个临界值。
5. **比较统计量与临界值：**如果统计量超过临界值，则拒绝假设；否则，接受假设。

**代码块：**

% 从正态总体中抽取样本
mu = 50;  % 总体均值
sigma = 10;  % 总体标准差
n = 100;  % 样本量
data = normrnd(mu, sigma, n, 1);

% 计算样本均值和标准差
sample_mean = mean(data);
sample_std = std(data);

% 假设检验：检验样本均值是否等于总体均值
alpha = 0.05;  % 显著性水平
[h, p] = ttest(data, mu);

% 输出结果
if h == 1
    fprintf('拒绝假设，样本均值与总体均值不同\n');
else
    fprintf('接受假设，样本均值与总体均值相同\n');
end

**逻辑分析：**

* `normrnd` 函数从正态总体中生成样本数据。
* `mean` 和 `std` 函数计算样本均值和标准差。
* `ttest` 函数执行 t 检验，检验样本均值是否等于总体均值。
* `h` 和 `p` 分别表示假设检验的结果（是否拒绝假设）和 p 值（假设成立的概率）。

# 3. MATLAB中的回归分析

### 3.1 回归模型的建立与评估

#### 3.1.1 模型拟合与参数估计

在MATLAB中，可以使用`fitlm`函数进行线性回归模型的拟合，该函数会返回一个`LinearModel`对象，其中包含模型的拟合参数和统计量。

% 导入数据
data = readtable('data.csv');

% 拟合线性回归模型
model = fitlm(data, 'y ~ x1 + x2');

% 查看模型参数
model.Coefficients.Estimate

对于非线性回归模型，可以使用`fitnlm`函数进行拟合，该函数会返回一个`NonlinearModel`对象，其中包含模型的拟合参数和统计量。

% 导入数据
data = readtable('data.csv');

% 拟合非线性回归模型
model = fitnlm(data, 'y ~ a * exp(-b * x)');

% 查看模型参数
model.Coefficients.Estimate

#### 3.1.2 模型验证与诊断

模型拟合后，需要对模型进行验证和诊断，以评估模型的性能和可靠性。常用的模型验证方法包括：

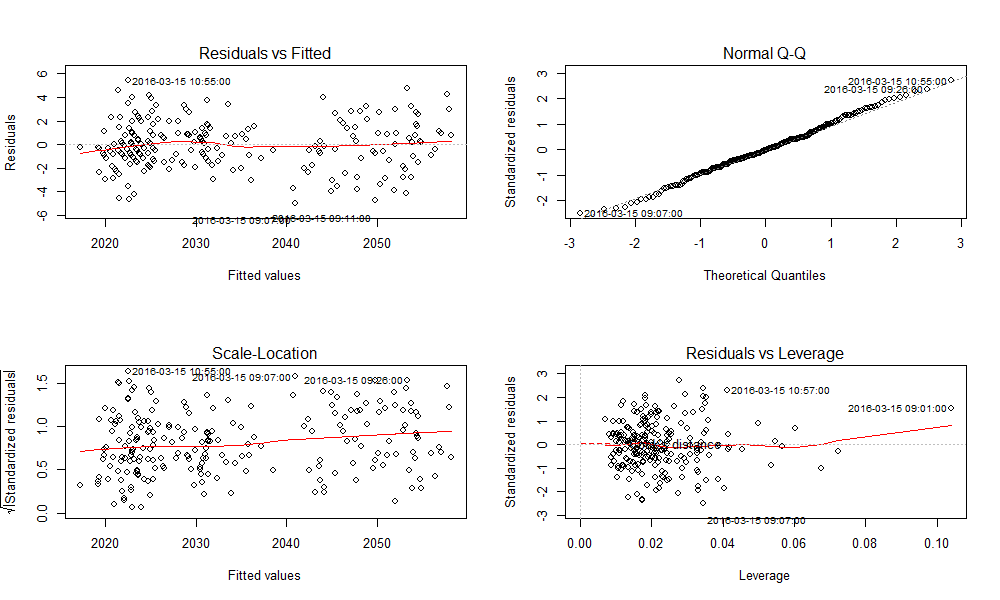
- **残差分析：**检查残差的分布是否符合正态分布，是否存在异方差性或自相关性。
- **交叉验证：**将数据集划分为训练集和测试集，使用训练集拟合模型，并使用测试集评估模型的预测性能。
- **信息准则：**使用赤池信息准则（AIC）或贝叶斯信息准则（BIC）等信息准则来比较不同模型的拟合优度。

% 残差分析
resid = model.Residuals.Raw;
histogram(resid);

% 交叉验证
cv = crossval(model, 'KFold', 10);
cv_results = crossval(model, 'KFold', 10, 'Metrics', 'mse');

% 信息准则
aic = model.AIC;
bic = model.BIC;

#