时间序列的协整与误差修正模型：长期关系分析，深度剖析

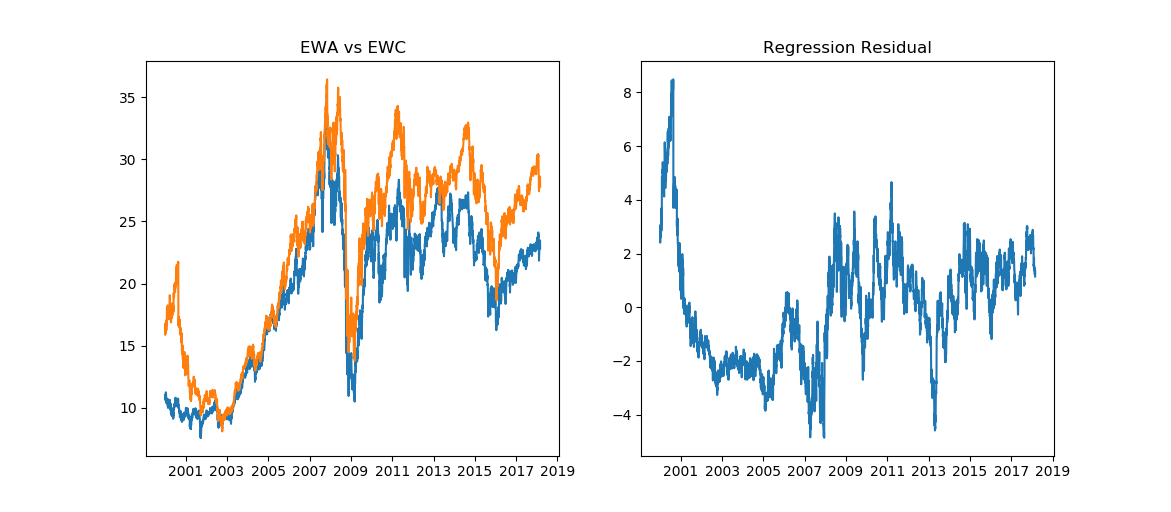
# 1. 时间序列与协整理论基础

在现代经济学和金融学的研究中，时间序列分析和协整理论是极其重要的分析工具。时间序列分析关注单个变量随时间变化的统计特性，而协整理论则针对两个或多个非平稳时间序列之间的长期稳定关系进行探究。

## 1.1 时间序列的概念与应用
时间序列是一组按照时间顺序排列的数据点，广泛应用于经济预测、金融分析、信号处理等领域。理解时间序列的特征，如趋势、季节性、循环和随机性，对于建立有效的预测模型至关重要。

## 1.2 协整的定义和直观理解
协整描述的是两个或多个非平稳时间序列之间的长期均衡关系。直观理解，即使每个时间序列自身表现出随机波动，它们之间的线性组合可能呈现稳定的长期趋势。例如，一个国家的出口总额和进口总额虽然各自波动，但可能随时间呈现共同增长的趋势。

## 1.3 协整理论的经济意义
在经济学中，协整理论有助于分析变量之间的长期关系，例如国家收入和消费支出之间的均衡关系。识别这种关系对于制定经济政策、进行市场预测和风险评估具有重要意义。通过协整分析，经济学家可以理解不同经济指标之间的相互作用，以及它们是如何在经济运行中相互调整以维持稳定状态的。

## 1.4 协整与误差修正模型(EMC)
协整与误差修正模型紧密相关。当序列协整时，我们可以构建EMC模型来解释它们之间的短期动态关系。EMC模型不仅包括了协整方程，还涉及误差修正机制，即在短期偏离长期均衡时，如何通过动态调整过程恢复长期均衡关系。该模型在理解和预测时间序列短期行为方面提供了更深层次的分析。

了解时间序列与协整理论基础为后续章节中关于统计检验、误差修正模型的建立和应用，以及软件实现等更深入的讨论奠定了坚实的理论基础。在实践中，这将指导我们更好地运用时间序列分析方法解决实际问题。

# 2. 协整关系的统计检验

## 2.1 协整概念及其数学描述

### 2.1.1 协整的定义和直观理解

在经济学和金融学中，许多变量是随时间变化的，它们可能不是平稳的，但是它们之间的关系可以是平稳的。协整是对两个或多个非平稳时间序列长期均衡关系的一种度量。直观上，如果两个或多个非平稳时间序列的某种线性组合是平稳的，那么这些时间序列就被认为是协整的。协整关系的发现可以帮助我们理解经济变量之间存在的长期稳定关系。

### 2.1.2 协整的数学模型和性质

协整关系可以用以下数学模型表示：
假设有两个非平稳的时间序列 \(X_t\) 和 \(Y_t\)，它们各自是非平稳的，但如果存在一组系数 \(\alpha\) 和 \(\beta\)，使得 \(Z_t = \alpha X_t + \beta Y_t\) 是平稳的，那么我们可以说 \(X_t\) 和 \(Y_t\) 是协整的。

协整关系具有以下性质：
- 协整关系意味着长期的均衡。
- 在短期，可能会出现偏离长期均衡的情况，但随着时间的推移，这些短期的偏离会被调整回来，以保持长期均衡状态。
- 协整向量可以用来构建误差修正模型（ECM），该模型将短期动态与长期均衡联系起来。

## 2.2 协整检验的方法论

### 2.2.1 Engle-Granger两步法

Engle-Granger两步法是检验两个序列协整关系的一种常见方法。这种方法包括以下步骤：
- **第一步**：使用普通最小二乘法（OLS）估计长期关系方程 \(Y_t = \alpha + \beta X_t + \epsilon_t\)，得到残差 \(\hat{\epsilon_t}\)。
- **第二步**：检验残差序列 \(\hat{\epsilon_t}\) 是否平稳。如果残差序列是平稳的，那么可以认为 \(X_t\) 和 \(Y_t\) 是协整的。

### 2.2.2 Johansen协整检验

Johansen协整检验是对于多于两个变量之间协整关系的检验。该方法基于向量自回归（VAR）模型，并使用似然比检验来决定协整向量的数量。Johansen检验通常包括以下步骤：
- 确定VAR模型的阶数。
- 使用特征根迹检验（Trace test）或最大特征值检验（Max test）来确定协整向量的数量。
- 如果存在协整向量，可以进一步估计协整参数和进行误差修正模型的建立。

### 2.2.3 其他协整检验方法

除了上述两种方法，还有其他一些协整检验方法。例如，Phillips-Ouliaris检验和GPH检验主要用于单一方程的协整关系检验，而Saikkonen和Lutkepohl提出了基于误差修正模型的协整检验。

## 2.3 协整检验的实践操作

### 2.3.1 实际数据的收集和预处理

在进行协整检验之前，需要收集相关的时间序列数据，并对其进行预处理。预处理可能包括：
- 数据清洗：去除异常值、缺失值。
- 数据变换：对数变换或差分变换以达到数据平稳。

### 2.3.2 应用统计软件进行协整检验

使用统计软件（如EViews、R、Stata等）可以帮助我们完成协整检验的过程。以下是使用R语言进行Engle-Granger协整检验的示例代码：

# 安装并加载urca包
install.packages("urca")
library(urca)

# 载入数据
data(treasury)  # 示例数据集

# 假设我们对序列"tnote3m"和"tbill3m"感兴趣
# 第一步，使用OLS估计长期关系
lm_result <- lm(tbill3m ~ tnote3m, data = treasury)

# 第二步，检验残差序列是否平稳
residuals <- resid(lm_result)
adf_test <- ur.df(residuals, type = "drift", lags = 1)
summary(urca:::summary(ur.df))

# 输出ADF检验的统计量和p值

以上代码首先使用`lm()`函数估计了两个时间序列的长期关系，然后使用`ur.df()`函数对残差进行了ADF检验。最后，通过调用`summary()`函数输出了ADF检验的详细结果，其中包括统计量和p值，从而可以判断残差序列是否平稳，进而决定是否接受协整关系的存在。

在本章节中，我们详细探讨了协整关系的概念，理论基础，检验方法，并通过R语言的实践操作向大家展示了如何执行实际的协整检验。接下来，我们将深入探讨误差修正模型（ECM），它是协整概念的一种重要应用，为我们提供了分析经济变量间短期波动和长期均衡关系的工具。

# 3. 误差修正模型（ECM）的建立和应用

## 3.1 ECM模型的理论框架

### 3.1.1 ECM模型的基本结构
误差修正模型（ECM）是一种特殊形式的统计模型，它结合了差分方程和协整关系，专门用于分析在非平稳时间序列中长期均衡关系的短期调整。ECM模型能够反映变量之间长期稳定的关系，并且能够解释当短期波动偏离长期均衡时的修正速度。

在基本结构上，ECM模型通常被写作一个动态的线性模型，包含了差分项和误差修正项。误差修正项基于之前时间点的非均衡误差。简而言之，模型可以形式化为：

\[ \Delta Y_t = \alpha + \beta \Delta X_t + \gamma (Y_{t-1} - \delta X_{t-1}) + \epsilon_t \]

其中，\(\Delta\) 表示差分操作，\(Y\) 和 \(X\) 是需要分析的两个时间序列变量，\(\alpha\)、\(\beta\)、\(\gamma\) 和 \(\delta\) 是模型参数，\(\epsilon_t\) 是误差项。

### 3.1.2 ECM模型的经济意义
ECM模型揭示了经济变量之间的短期和长期动态调整过程。当模型中的变量因为短期冲击而偏离长期均衡状态时，误差修正项决定了调整的速度和方向。这使得 ECM 不仅能捕捉到变量间即时的动态变化，还能体现出如何回归到均衡状态。

例如，在金融领域，两个金融资产价格的长期均衡关系可能会因为短期的市场波动而发生偏离，而 ECM 可以提供一个框架来分析这种偏离是如何在接下来的时间内得到纠正的。

## 3.2 ECM模型的参数估计和检验

### 3.2.1 参数估计方法
估计 ECM 模型参数的一个常见方法是使用两阶段最小二乘法（2SLS）。首先，需要确定协整关系，即估计长期均衡关系的参数。然后，这些估计得到的长期参数可以被用来构造误差修正项，并将该误差修正项作为解释变量之一进行回