【PMSM参数调优攻略】：控制系统优化的必经之路


# 摘要
本文探讨了永磁同步电机（PMSM）的参数调优技术，从理论基础到实践应用进行了全面分析。首先介绍了PMSM参数调优的理论基础和控制系统的关键参数解析，重点关注电机参数的理论模型、关键参数定义、性能影响以及参数测量与识别技术。随后，通过具体的实践案例，阐述了参数调优前的系统评估、调优工具和技术应用以及实际调优过程。进一步探讨了PMSM参数调优的高级技术，包括自适应参数调整算法、智能优化算法的应用以及参数调优与系统集成的关系。最后，文章展望了PMSM参数调优的未来趋势，特别是在新型材料、数字化与智能制造背景下的发展方向，以及人工智能技术与PMSM参数优化的融合潜力。

# 关键字
永磁同步电机；参数调优；理论模型；自适应控制；智能优化算法；系统集成

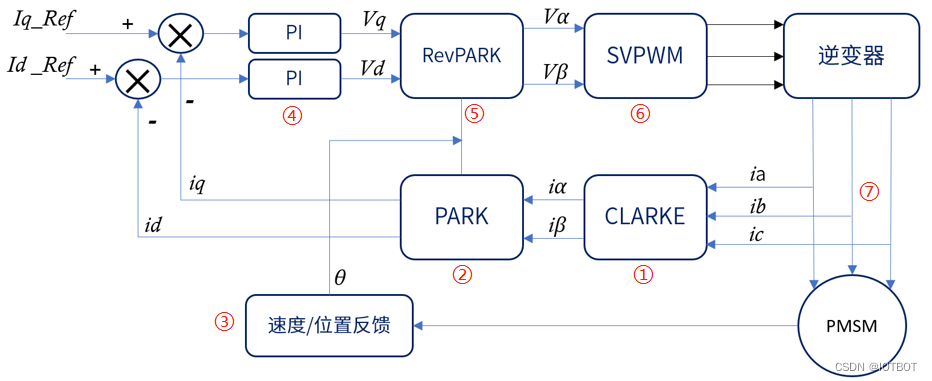
参考资源链接：[永磁同步电机FOC控制算法详解与实现](https://wenku.csdn.net/doc/21d3uutvv3?spm=1055.2635.3001.10343)
# 1. PMSM参数调优的理论基础

理解永磁同步电机（PMSM）参数调优的理论基础是提升电机性能与效率的关键起点。本章将深入探讨PMSM参数优化的基本原理、控制策略以及理论与实践相结合的重要性。

## 1.1 电机参数优化的必要性
电机参数优化是一个关键过程，它涉及调整电机控制系统中的关键参数以达到最佳性能。这些参数可能包括电机控制算法中的比例-积分-微分（PID）系数、电机的电阻、电感以及磁通量等。

## 1.2 PMSM的工作原理
PMSM利用永磁体产生磁场，与定子中的旋转磁场相互作用产生驱动力。优化这些磁场的相互作用，以确保电机在不同工作状态下维持高效和低损耗。

## 1.3 参数调整的理论框架
在理论层面，电机的动态性能和效率可以通过控制参数的变化来调优，这通常涉及到电机的数学模型。对电机模型参数的精确识别与调整，可以显著提高电机的响应速度、控制精度和运行稳定性。

通过这一系列的理论介绍，读者将对PMSM参数调优的必要性、工作原理及其理论框架有一个初步的了解，为深入学习后续章节内容奠定基础。

# 2. PMSM控制系统的关键参数解析

在现代电机控制系统中，永磁同步电机（PMSM）以其高效率、高转矩密度和良好的控制性能成为许多精密驱动系统的首选。为了充分发挥PMSM的优势，理解并优化其关键参数至关重要。本章将深入探讨PMSM电机的理论模型、参数调整对性能的影响以及参数的测量和识别技术。

## 2.1 电机参数的理论模型

### 2.1.1 PMSM电机的基本原理

PMSM电机的工作原理基于永磁体产生的恒定磁场与电枢绕组中交流电流相互作用，产生旋转磁场，从而驱动电机旋转。其结构通常包括定子、转子（永久磁铁）、电枢绕组、转轴和支架。PMSM电机可以采用三相或单相供电，并且通常需要一个变频驱动器来控制其速度和扭矩。

在三相PMSM电机中，定子上的三相绕组与一个交流电源相连，产生旋转磁场，其空间角度与电流的相位一致。转子上的永久磁铁因与旋转磁场的相互作用而产生力矩，推动电机转动。在理想情况下，当电机达到同步速度时，转子磁场与定子磁场的相对运动停止，电流仅用于克服机械损耗和铁耗，不再产生额外的转矩。

### 2.1.2 关键参数的定义和作用

PMSM电机的关键参数包括但不限于电阻、电感、极对数、额定功率、额定转速、额定扭矩、饱和磁通密度、转子惯量等。这些参数直接关系到电机的性能，对电机控制系统的设计和优化至关重要。

- 电阻和电感决定了电流的流通特性和响应速度。
- 极对数影响电机的同步速度和转矩特性。
- 额定功率和额定转速定义了电机的额定工作状态。
- 额定扭矩和饱和磁通密度决定了电机的负载能力和磁性能。
- 转子惯量则决定了电机的动态响应速度和惯性特性。

对这些参数的深入理解和精确控制，是实现PMSM控制系统高性能运行的基础。

## 2.2 参数调整对性能的影响

### 2.2.1 力矩和转速的参数影响

PMSM电机的力矩和转速是电机控制系统设计中关注的重点。调整电枢电流、磁通和极对数等参数可以显著影响电机的力矩输出和转速特性。

- 电枢电流的增加会导致转矩的提升，但同时也会增加电机的损耗和温升。
- 调整磁通密度，特别是在磁通弱化的区域，可以改善电机的启动特性和低速运行性能。
- 极对数直接影响电机的同步速度，极对数的增加会导致同步速度的下降。

因此，参数的综合调整需要考虑性能提升与系统稳定性的平衡。

### 2.2.2 能效和温升的参数分析

能效和温升是电机控制系统设计中不可忽视的重要参数。高能效意味着电机在运行时能量损失更少，而温升管理则关系到电机的安全稳定运行。

- 电阻是影响能效的重要参数之一，减小电阻值可以降低铜损，提高电机效率。
- 电感的增加有助于减少交流电机中的漏感，从而降低磁损，提升效率。
- 电机的温升与电机的损耗密切相关，包括铜损和铁损。通过优化电机设计和控制策略，可以有效控制温升，延长电机使用寿命。

分析和优化这些参数，需要综合考虑电机的电气特性、热特性和控制策略。

## 2.3 参数测量与识别技术

### 2.3.1 参数测量的方法和工具

准确地测量PMSM电机的关键参数对于评估电机性能和优化控制系统至关重要。常用的测量方法包括阻抗测量、功率分析、转矩和速度传感器等。

- 阻抗测量通常用于获取定子绕组的电阻和电感值，这是电机参数测量的基础。
- 功率分析通过测量电机输入和输出的功率，计算电机的效率和损耗。
- 转矩和速度传感器可以提供实时的转矩和转速数据，对于调节控制策略和监控电机运行状态至关重要。

现代测量工具如电参数分析仪和旋转扭矩测量系统，为电机参数测量提供了高精度和高稳定性的解决方案。

### 2.3.2 参数识别算法和实践

参数识别算法是一种从电机运行数据中识别出电机参数的方法，它有助于构建电机的精确模型，并在控制系统中实现参数的实时或近实时更新。

- 最小二乘法是一种常用的参数识别算法，适用于线性系统参数的估计。
- 遗传算法和粒子群优化等智能优化算法则适用于非线性系统的参数识别。
- 在实际应用中，参数识别往往与控制系统相结合，通过实时数据处理和反馈调节，实现参数的动态调整。

电机参数识别过程的准确性直接影响到控制系统设计的可靠性和电机性能的优化效果。

以下是本章节中为实现章节目标所用到的代码块、表格和mermaid流程图。

### 代码块分析

为了演示如何测量电机参数，例如电阻和电感，我们可以使用一个简单的交流电阻测量仪的伪代码示例。

# 电机参数测量伪代码
def measure_resistance(voltage, current):
    """测量电机电阻"""
    resistance = voltage / current
    return resistance

def measure_inductance(voltage_change, current_change, time_change):
    """测量电机电感"""
    inductance = (voltage_change / current_change) * time_change
    return inductance

# 测量电压和电流
voltage = 5.0  # V
current = 2.5  # A
voltage_change = 0.2  # V
current_change = 0.05  # A
time_change = 0.001  # s

# 计算电阻和电感值
motor_resistance = measure_resistance(voltage, current)
motor_inductance = measure_inductance(voltage_change, current_change, time_change)

print(f"电机电阻: {motor_resistance} Ohm")
print(f"电机电感: {motor_inductance} Henry")

### 表格展示

电机参数测量的常用方法可以概括如下：

| 测量参数 | 方法 | 优势 | 注意事项 |
|----------|------|-------|----------|
| 电阻 | 直流电压和电流测量 | 准确、易于实现 | 需要直流电源和电流表 |
| 电感 | 交流电压变化和电流变化 | 可在运行中测量 | 需要交流电源和示波器 |
| 功率 | 输入输出功率分析法 | 准确度高 | 需要功率分析仪 |
| 转矩和速度 | 传感器测量 | 高精度实时数据 | 需要专用传感器和处理单元 |

### Mermaid 流程图

下图为参数测量与识别技术的流程图：

graph LR
A[开始参数测量] --> B[测量电机电阻]
B --> C[测量电机电感]
C --> D[测量电机功率]
D --> E[安装传感器测量转矩和速度]
E --> F[数据处理与参数识别]
F --> G[控制系统参数优化]
G --> H[结束]

### 参数识别算法伪代码

import numpy as np

def least_squares_estimation(data_points, model_function):
    """
    最小二乘法参数估计
    data_points: 数据点元组(x, y)
    model_function: 模型函数，例如线性模型 y = ax + b
    """
    # 将数据转换为NumPy数组
    x_data, y_data = zip(*data_points)
    x_data = np.array(x_data).reshape(-1, 1)
    y_data = np.array(y_data)

    # 计算模型参数
    model_params = np.linalg.lstsq(x_data, y_data, rcond=None)[0]

    return model_params

# 使用最小二乘法估计模型参数
data_points = [(1, 2), (2, 3), (3, 4)]  # 示例数据点
linear_model_params = least_squares_estimation(data_points, model_function=lambda x: x[0] * a + b)

print(f"线性模型参数估计结果: a = {linear_model_p