模型压缩科学：PyTorch量化技术的深度解析与应用

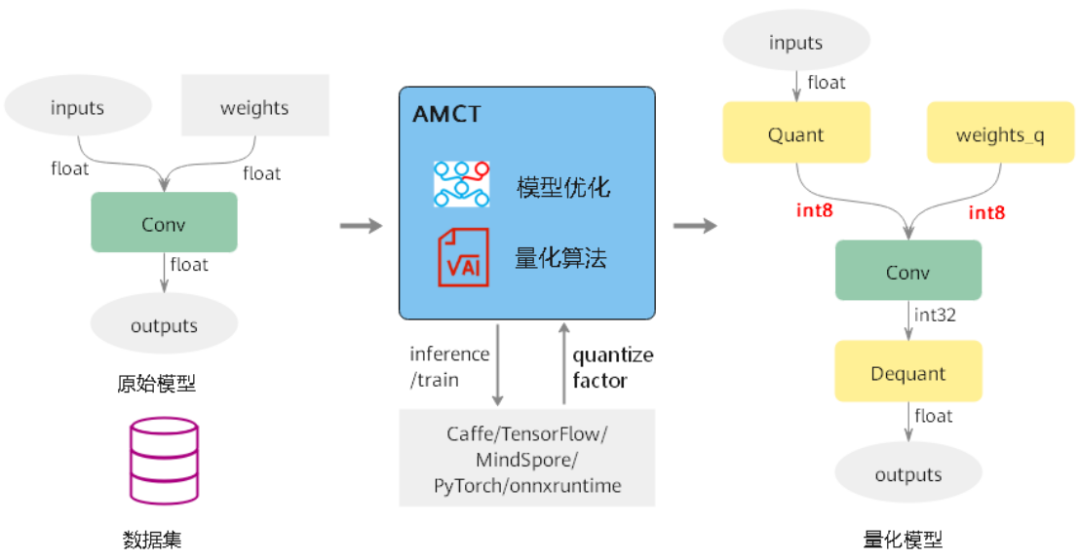
# 1. PyTorch量化技术概述

量化技术是深度学习模型优化的一个重要方向，它通过减少模型参数和激活值的位宽，以达到降低计算资源消耗和提升模型推理速度的目的。对于那些需要在边缘设备或移动平台上部署的深度学习应用来说，量化技术提供了显著的性能改进。在PyTorch中，量化工具箱提供了一套丰富的API和接口，使得开发者能够轻松地将传统的浮点模型转化为量化模型。本章旨在引导读者了解量化技术的基础概念，并概述在PyTorch中实施量化技术的准备工作。在后续章节中，我们将深入探讨量化技术的理论基础、量化实践、部署应用、性能评估以及面临的挑战与未来趋势。

# 2. ```
# 第二章：理论基础与量化原理
## 2.1 深度学习模型的量化基础
### 2.1.1 量化的基本概念和优势
量化是一种减少深度学习模型中参数和激活所需的存储空间和计算资源的技术。通过将浮点数参数转换为较低精度（如int8或int16）的整数参数，量化能够大幅减少模型的大小，从而使得模型可以在资源受限的环境中运行，例如移动设备或边缘计算设备。量化的优势主要体现在以下几个方面：

- **减少模型大小**：通过整数表示参数和激活，模型占用的存储空间将显著减小，便于模型在资源有限的设备上部署。
- **降低计算复杂度**：整数运算在硬件上通常比浮点运算更快，更省电，因此量化模型在运行时的延迟会降低，功耗也会减少。
- **提升内存带宽效率**：整数操作能够更有效地利用CPU/GPU的内存带宽，因为量化后的数据通常需要更少的内存访问。

尽管量化带来了这些优势，但它也可能带来模型精度的下降。在量化过程中，需要权衡模型的精度和性能，以满足特定应用的需求。

### 2.1.2 量化对模型精度和性能的影响
量化过程涉及到的精度损失主要来源于两方面：量化精度和舍入误差。量化精度指在将浮点数映射到整数时可能丢失的信息量，而舍入误差是指在量化和反量化过程中不可避免的数值近似误差。模型精度可能下降的原因可以总结如下：

- **参数空间的限制**：量化将连续的浮点数值空间映射到离散的整数空间，这导致了潜在的信息损失。
- **舍入误差**：在量化和反量化（将整数值映射回浮点数值）过程中，由于数值范围和精度的限制，不可避免地引入了误差。
- **数据分布的偏移**：某些层的激活数据分布可能会因为量化而改变，这可能影响模型训练过程中权重的更新。

为了最大限度地减少量化对模型精度的影响，通常需要在训练过程中应用特定的技术，如量化感知训练（Quantization-Aware Training, QAT），这将在后续章节中详细讨论。此外，混合精度量化策略，即仅对模型的一部分进行量化，也被证明是保持模型精度的有效方法。

## 2.2 量化方法的分类
### 2.2.1 权重量化与激活量化
量化可以应用在模型的权重（参数）或激活上，这两种情况各有其特点和应用场景。

- **权重量化**：通常权重量化可以对模型大小进行显著缩减，因为权重在整个网络中是共享的，一个小的量化误差可以被整个网络分摊。权重量化尤其适用于模型部署阶段。
- **激活量化**：激活量化在推理阶段对神经网络的中间输出进行量化。由于激活通常对数值范围和分布较为敏感，激活量化可能导致较大的精度损失。

在实际应用中，权重量化和激活量化常常被联合使用，以达到最佳的性能和精度平衡。

### 2.2.2 静态量化与动态量化
根据量化过程是否依赖于输入数据，可以将量化分为静态量化和动态量化。

- **静态量化**：在静态量化中，量化参数是在模型训练完成后确定的，并且在整个推理过程中保持不变。这种方式易于部署，因为不需要在推理时进行额外的计算，但可能无法充分利用模型的动态范围。
- **动态量化**：动态量化在每次推理时根据输入数据动态确定量化参数。这种量化策略能够更好地适应数据的变化，但增加了运行时的计算负担和复杂性。

### 2.2.3 混合量化策略
混合量化策略结合了静态量化和动态量化的优点，分别对模型的权重和激活采取不同的量化方法。通常情况下，权重采用静态量化，以保持模型的紧凑性和部署的高效性；而激活采用动态量化，以便更好地适应输入数据的动态范围。

混合量化可以灵活地根据模型的具体需求和部署环境进行调整。在某些应用场景中，通过精细调整量化策略，可以在保持模型精度的同时显著提高模型的推理速度和效率。

## 2.3 量化算法与数学原理
### 2.3.1 量化参数的数学模型
量化可以视为一个从浮点数值空间到整数数值空间的映射过程。设浮点数范围为 \([x_{min}, x_{max}]\)，可以通过以下步骤将一个浮点数值 \(x\) 映射到量化后的整数 \(q\)：

1. **确定量化级别**：确定使用的整数位数 \(b\)（如8位，即 \(b=8\)），并计算该位数可以表示的数值范围大小 \(2^b\)。
2. **确定量化尺度**：计算量化尺度 \(s = \frac{2^b - 1}{x_{max} - x_{min}}\)。
3. **量化**：得到量化后的整数值 \(q = \text{clip}\left(\left\lfloor \frac{x - x_{min}}{s} + 0.5 \right\rceil, 0, 2^b - 1\right)\)。

这里，\(\text{clip}(\cdot, a, b)\) 函数用于限制数值在 \([a, b]\) 范围内，\(\lfloor\cdot\rceil\) 表示向下取整（或者四舍五入）操作。

### 2.3.2 精度校准与量化误差分析
量化误差主要来自于舍入误差，可以通过精度校准来最小化这种误差。精度校准通常涉及以下步骤：

1. **收集统计数据**：在训练或推理阶段收集权重和激活的分布统计数据，如最大值、最小值等。
2. **确定量化参数**：基于统计数据确定量化参数，如量化范围、量化尺度和量化偏移量。
3. **应用校准技术**：通过特定的校准技术（例如缩放和平移），使得量化的整数尽可能接近原始的浮点数值。

为了准确评估量化误差，可以利用统计分析方法，比如计算量化的均方误差（MSE）或最大绝对误差（MAE）等指标。通过这些指标，研究人员可以评估量化的精度损失，并进行相应的调整来优化量化模型。

在实际操作中，通常需要综合考虑多种因素来选择合适的量化算法。例如，在设计量化算法时，需要考虑到目标硬件的特性（如处理器的算术逻辑单元ALU支持的整数运算类型），以及实际应用中对精度和性能的具体要求。

# 3. PyTorch量化技术实践

在这一章中，我们将在PyTorch框架内深入探讨量化技术的实现，并通过具体的实例分析量化技术对深度学习模型的具体影响和优化。

## 3.1 PyTorch中的量化工具与接口

### 3.1.1 量化API的使用方法

PyTorch提供了易于使用的量化API，这些API允许开发者在不同层次上对模型进行量化操作。量化API的主要组件包括：

- `torch.quantization.QuantStub`：用于将模型的输入转换为量化形式。
- `torch.quantization.DeQuantStub`：用于将模型的输出从量化形式转换回常规形式。
- `torch.quantization.Quantizer`：执行量化操作，将浮点数参数转换为定点数参数。

为了使用这些API，开发者需要定义一个继承自`torch.nn.Module`的类，并在其中插入`QuantStub`和`DeQuantStub`。在模型转换为量化模型后，可以使用`prepare`和`convert`方法来执行量化感知训练和模型的转换。

### 3.1.2 基于torch.quantization模块的实战

使用PyTorch量化模块的一个实战案例是量化一个简单的神经网络。以下代码展示了一个PyTorch模型的量化过程：

import torch
import torch.nn as nn
from torch.quantization import QuantStub, DeQuantStub, quantize

class SimpleModel(nn.Module):
def __init__(self):
super(SimpleModel, self).__init__()
self.quant = QuantStub()
self.fc = nn.Linear(10, 1)
self.dequant = DeQuantStub()

def forward(self, x):
x = self.quant(x)
x = self.fc(x)
return self.dequant(x)

# 创建模型实例
model = SimpleModel()

# 准备模型进行量化
model.qconfig = torch.quantization.get_default_qconfig('fbgemm')
torch.backends.quantized.engine = 'fbgemm'
model = torch.quantization.prepare(model, inplace=False)

# 使用校准数据进行模拟推理，以便确定量化的数值范围
with torch.no_grad():