揭秘MATLAB行列式计算实战奥秘：从基础到大师级应用

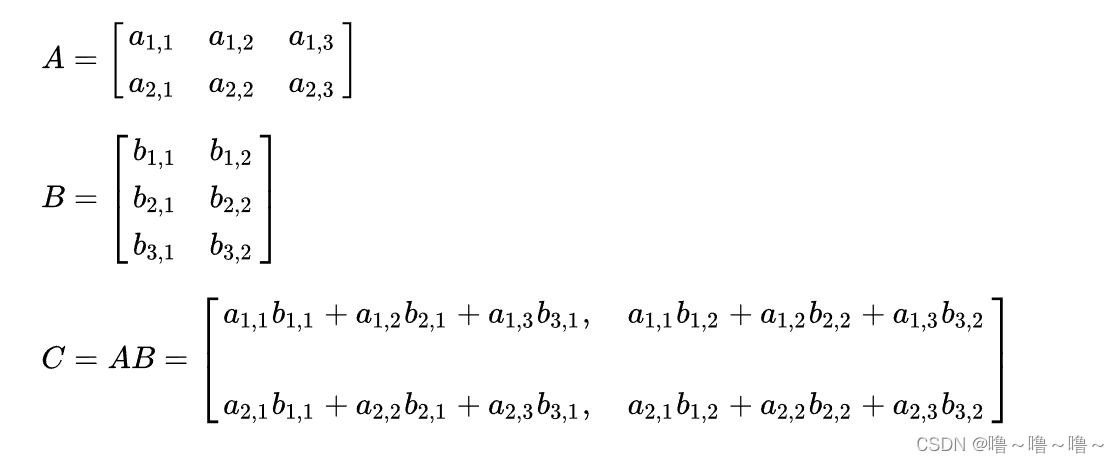
# 1. 行列式基础**

行列式是线性代数中一个重要的概念，它可以用来表示矩阵的行列式。行列式的值可以用来判断矩阵是否可逆，也可以用来求解线性方程组。

**行列式的定义**

行列式是一个n阶方阵的标量值。对于一个n阶方阵A，其行列式记为det(A)。行列式的值等于A中所有n阶子式的代数余子式的和。

**行列式的性质**

行列式具有以下性质：

* 行列式的转置等于其本身，即det(A^T) = det(A)
* 行列式的行列式乘积等于行列式的乘积，即det(AB) = det(A)det(B)
* 如果行列式中有一行或一列全为0，则行列式的值为0
* 如果行列式中有一行或一列乘以一个常数，则行列式的值乘以这个常数

# 2.1 行列式的定义和性质

### 2.1.1 行列式的概念和几何意义

行列式是一个与矩阵相关联的标量值，它描述了矩阵的某些性质。它由矩阵元素按照特定规则组合而成。

**定义：**

设 A 是一个 n×n 方阵，其元素为 aij。行列式 det(A) 定义为：

det(A) = ∑(±)a1j1a2j2...anjn

其中，求和遍历所有 n! 个可能的 j1, j2, ..., jn 的排列，并且符号 (±) 取决于排列的奇偶性。

**几何意义：**

n×n 方阵的行列式表示了该矩阵所表示的线性变换对 n 维空间中单位立方体的体积的缩放因子。行列式为正，表示线性变换保持体积；行列式为负，表示线性变换反转体积；行列式为零，表示线性变换将体积塌陷为零。

### 2.1.2 行列式的基本性质

行列式具有以下基本性质：

* **行列式交换行或列的符号：**交换行列式的任意两行（或列），行列式的符号改变。
* **行列式乘以一个常数：**行列式乘以一个常数，结果等于原行列式乘以该常数。
* **行列式加法：**行列式的任意两行（或列）相加，结果等于行列式两行（或列）的行列式之和。
* **行列式的乘法：**两个矩阵的行列式相乘，等于两个矩阵相乘的行列式。
* **行列式逆矩阵：**行列式不为零的矩阵存在逆矩阵，且逆矩阵的行列式等于原矩阵行列式的倒数。
* **行列式转置：**行列式的转置等于原行列式。

# 3. 行列式在MATLAB中的应用

### 3.1 行列式的计算

行列式在MATLAB中可以通过多种函数进行计算，其中最常用的函数是`det()`和`lu()`。

#### 3.1.1 det()函数

`det()`函数用于计算方阵的行列式。其语法为：

det(A)

其中，`A`为方阵。

**代码块：**

% 计算方阵A的行列式
A = [1 2 3; 4 5 6; 7 8 9];
det_A = det(A);

% 输出行列式
disp(['行列式det(A) = ' num2str(det_A)]);

**逻辑分析：**

该代码首先定义了一个3x3方阵`A`，然后使用`det()`函数计算其行列式，并将结果存储在变量`det_A`中。最后，输出行列式的值。

**参数说明：**

* `A`：要计算行列式的方阵。

#### 3.1.2 lu()函数

`lu()`函数用于对方阵进行LU分解，并返回分解后的下三角矩阵和上三角矩阵。其语法为：

[L, U] = lu(A)

其中，`A`为方阵，`L`为下三角矩阵，`U`为上三角矩阵。

**代码块：**

% 对方阵A进行LU分解
[L, U] = lu(A);

% 输出下三角矩阵和上三角矩阵
disp('下三角矩阵L：');
disp(L);
disp('上三角矩阵U：');
disp(U);

**逻辑分析：**

该代码使用`lu()`函数对方阵`A`进行LU分解，并输出分解后的下三角矩阵`L`和上三角矩阵`U`。

**参数说明：**

* `A`：要进行LU分解的方阵。

### 3.2 行列式的求逆

在MATLAB中，行列式的求逆可以通过`inv()`和`pinv()`函数实现。

#### 3.2.1 inv()函数

`inv()`函数用于计算非奇异方阵的逆矩阵。其语法为：

inv(A)

其中，`A`为非奇异方阵。

**代码块：**

% 计算非奇异方阵A的逆矩阵
A = [2 3; 4 5];
inv_A = inv(A);

% 输出逆矩阵
disp(['逆矩阵inv(A) = ']);
disp(inv_A);

**逻辑分析：**

该代码定义了一个2x2非奇异方阵`A`，并使用`inv()`函数计算其逆矩阵，并将结果存储在变量`inv_A`中。最后，输出逆矩阵。

**参数说明：**

* `A`：要计算逆矩阵的非奇异方阵。

#### 3.2.2 pinv()函数

`pinv()`函数用于计算奇异方阵的伪逆矩阵。其语法为：

pinv(A)

其中，`A`为奇异方阵。

**代码块：**

% 计算奇异方阵A的伪逆矩阵
A = [1 2; 3 4; 5 6];
pinv_A = pinv(A);

% 输出伪逆矩阵
disp(['伪逆矩阵pinv(A) = ']);
disp(pinv_A);

**逻辑分析：**

该代码定义了一个3x2奇异方阵`A`，并使用`pinv()`函数计算其伪逆矩阵，并将结果存储在变量`pinv_A`中。最后，输出伪逆矩阵。

**参数说明：**

* `A`：要计算伪逆矩阵的奇异方阵。

### 3.3 行列式的特征值和特征向量

行列式的特征值和特征向量可以通过`eig()`和`svd()`函数求解。

#### 3.3.1 eig()函数

`eig()`函数用于计算方阵的特征值和特征向量。其语法为：

[V, D] = eig(A)

其中，`A`为方阵，`V`为特征向量矩阵，`D`为特征值矩阵。

**代码块：**

% 计算方阵A的特征值和特征向量
A = [2 3; 4 5];
[V, D] = eig(A);

% 输出特征值和特征向量
disp('特征值D：');
disp(D);
disp('特征向量V：');
disp(V);

**逻辑分析：**

该代码定义了一个2x2方阵`A`，并使用`eig()`函数计算其特征值和特征向量。特征值存储在变量`D`中，特征向量存储在变量`V`中。最后，输出特征值和特征向量。

**参数说明：**

* `A`：要计算特征值和特征向量的方阵。

#### 3.3.2 svd()函数

`svd()`函数用于计算奇异值分解（SVD），并返回奇异值、左奇异向量和右奇异向量。其语法为：

[U, S, V] = svd(A)

其中，`A`为矩阵，`U`为左奇异向量矩阵，`S`为奇异值矩阵，`V`为右奇异向量矩阵。

**代码块：**

% 计算矩阵A的奇异值分解
A = [1 2; 3 4; 5 6];
[U, S, V] = svd(A);

% 输出奇异值、左奇异向量和右奇异向量
disp('奇异值S：');
disp(S);
disp('左奇异向量U：');
disp(U);
disp('右奇异向量V：');
disp(V);

**逻辑分析：**

该代码定义了一个3x2矩阵`A`，并使用`svd()`函数计算其奇异值分解。奇异值存储在变量`S`中，左奇异向量存储在变量`U`中，右奇异向量存储在变量`V`中。最后，输出奇异值、左奇异向量和右奇异向量。

**参数说明：**

* `A`：要进行奇异值分解的矩阵。

# 4. 行列式在工程中的应用

### 4.1 线性方程组求解

行列式在求解线性方程组中有着重要的作用。对于一个系数矩阵为 A 的 n 元线性方程组：

Ax = b

其中，A 是一个 n 阶方阵，x 是未知数列，b 是常数列。

#### 4.1.1 克莱姆法则求解

克莱姆法则是一种求解线性方程组的经典方法，它利用行列式来计算每个未知数的值。对于方程组 Ax = b，克莱姆法则的公式如下：

x_i = det(A_i) / det(A)

其中，A_i 是将 b 列替换为第 i 列的系数矩阵，det(A) 是系数矩阵 A 的行列式。

**代码块：**

% 系数矩阵 A
A = [2, 1, 1; 4, 3, 2; 8, 7, 4];

% 常数列 b
b = [1; 2; 3];

% 求解未知数 x
x = zeros(size(A, 1), 1);
for i = 1:size(A, 1)
    A_i = A;
    A_i(:, i) = b;
    x(i) = det(A_i) / det(A);
end

% 输出结果
disp('未知数 x 的值：');
disp(x);

**逻辑分析：**

这段代码使用克莱姆法则求解线性方程组。它首先创建系数矩阵 A 和常数列 b。然后，它使用 for 循环遍历未知数，并为每个未知数计算 A_i 和 det(A_i)。最后，它使用 det(A_i) / det(A) 计算每个未知数的值。

#### 4.1.2 矩阵求逆求解

另一种求解线性方程组的方法是使用矩阵求逆。对于方程组 Ax = b，如果系数矩阵 A 是可逆的，则可以将其求逆并得到：

x = A^-1 * b

其中，A^-1 是系数矩阵 A 的逆矩阵。

**代码块：**

% 系数矩阵 A
A = [2, 1, 1; 4, 3, 2; 8, 7, 4];

% 常数列 b
b = [1; 2; 3];

% 求解未知数 x
x = inv(A) * b;

% 输出结果
disp('未知数 x 的值：');
disp(x);

**逻辑分析：**

这段代码使用矩阵求逆求解线性方程组。它首先创建系数矩阵 A 和常数列 b。然后，它使用 inv() 函数求出系数矩阵 A 的逆矩阵。最后，它使用 inv(A) * b 计算未知数 x 的值。

### 4.2 线性变换

行列式在研究线性变换中也扮演着重要的角色。对于一个线性变换 T：V → W，其变换矩阵为 A，则 T 的行列式 det(A) 具有以下性质：

* **行列式不为零：**如果 det(A) ≠ 0，则 T 是一个可逆变换，即存在逆变换 T^-1。
* **行列式为零：**如果 det(A) = 0，则 T 是一个不可逆变换，即不存在逆变换 T^-1。

#### 4.2.1 矩阵的相似性

两个矩阵 A 和 B 是相似的，当且仅当存在一个可逆矩阵 P，使得：

B = P^-1 * A * P

相似的矩阵具有相同的行列式，即 det(A) = det(B)。

**代码块：**

% 矩阵 A
A = [2, 1; 4, 3];

% 矩阵 B
B = [3, 2; -1, 1];

% 可逆矩阵 P
P = [1, 1; 1, 2];

% 判断 A 和 B 是否相似
if isequaln(B, P^-1 * A * P)
    disp('矩阵 A 和 B 相似。');
else
    disp('矩阵 A 和 B 不相似。');
end

% 输出行列式
disp('矩阵 A 的行列式：');
disp(det(A));
disp('矩阵 B 的行列式：');
disp(det(B));

**逻辑分析：**

这段代码判断两个矩阵 A 和 B 是否相似。它首先创建矩阵 A、B 和可逆矩阵 P。然后，它使用 isequaln() 函数比较 B 和 P^-1 * A * P 是否相等。如果相等，则输出矩阵 A 和 B 相似；否则，输出矩阵 A 和 B 不相似。最后，它输出矩阵 A 和 B 的行列式。

#### 4.2.2 矩阵的特征值和特征向量

一个矩阵的特征值是其行列式为零时的值。特征向量是与特征值对应的非零向量，满足：

A * v = λ * v

其中，A 是矩阵，v 是特征向量，λ 是特征值。

**代码块：**

% 矩阵 A
A = [2, 1; 4, 3];

% 求解特征值和特征向量
[V, D] = eig(A);

% 输出特征值
disp('特征值：');
disp(diag(D));

% 输出特征向量
disp('特征向量：');
disp(V);

**逻辑分析：**

这段代码求解矩阵 A 的特征值和特征向量。它使用 eig() 函数计算特征值和特征向量。特征值存储在对角矩阵 D 中，特征向量存储在矩阵 V 中。

# 5. 行列式计算的进阶技巧**

**5.1 行列式的多重积分**

**5.1.1 行列式的积分表示**

行列式可以表示为一个多重积分，其中积分范围是行列式的阶数。对于一个n阶行列式，其积分表示为：

det(A) = ∫...∫ A(x₁, x₂, ..., xₙ) dx₁ dx₂ ... dxₙ

其中，A(x₁, x₂, ..., xₙ) 是行列式A的元素在积分变量x₁, x₂, ..., xₙ下的函数。

**5.1.2 数值积分方法**

计算行列式的多重积分可以使用数值积分方法，例如：

* 蒙特卡罗积分
* 辛普森积分
* 高斯积分

这些方法将积分区域划分为小的子区域，并对每个子区域进行积分，然后将结果相加得到近似值。

**5.2 行列式的渐近展开**

**5.2.1 行列式的拉普拉斯展开**

拉普拉斯展开是一种计算行列式的递归方法，它将行列式展开为子行列式的和。对于一个n阶行列式，其拉普拉斯展开为：

det(A) = ∑ᵢ=₁ⁿ (-1)ⁱ+¹ Aᵢⱼ det(Aᵢⱼ)

其中，Aᵢⱼ是A的i行j列的余子式。

**5.2.2 行列式的行列式展开**

行列式展开是一种将行列式展开为行列式的乘积的方法。对于一个n阶行列式，其行列式展开为：

det(A) = ∏ᵢ=₁ⁿ det(Aᵢ)

其中，Aᵢ是A的第i个主子式。

**5.3 行列式的应用于组合数学**

**5.3.1 行列式的组合意义**

行列式可以表示为一个组合计数，它表示n个元素排列的总数。对于一个n阶行列式，其组合意义为：

det(A) = ∑(π ∈ Sₙ) sgn(π) ∏ᵢ=₁ⁿ Aᵢπ(ᵢ)

其中，Sₙ是n个元素的全排列集合，sgn(π)是排列π的符号，Aᵢπ(ᵢ)是行列式A中第i行第π(i)列的元素。

**5.3.2 行列式的计数问题**

行列式可以用来解决组合计数问题，例如：

* 计算n个元素中r个元素的组合数
* 计算n个元素中r个元素的排列数
* 计算n个元素中r个元素的循环排列数