MATLAB行列式计算与矩阵论：深入理解矩阵与行列式的紧密关系

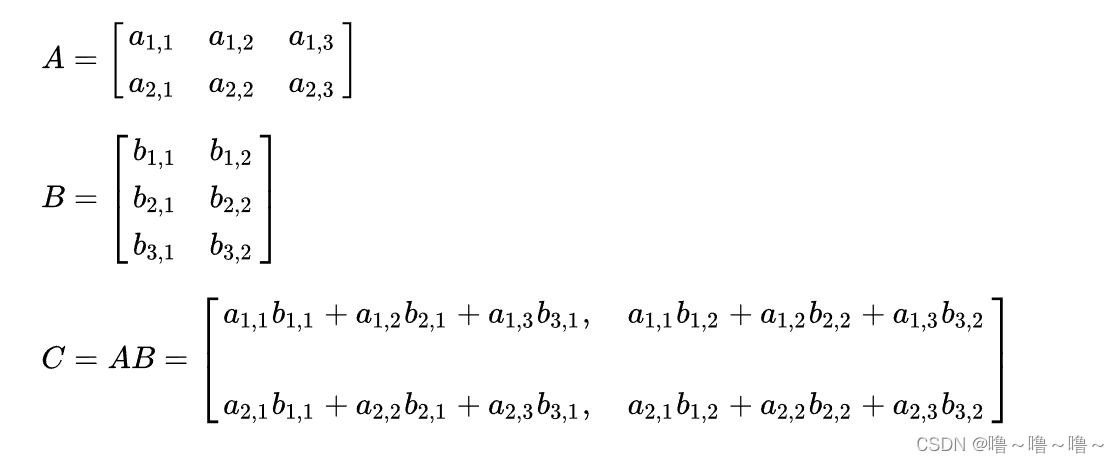
# 1. 矩阵与行列式的基础**

**1.1 矩阵的概念、运算和性质**

矩阵是一种矩形数组，由元素排列而成。矩阵的运算包括加减法、乘法、转置和求逆。矩阵具有许多性质，如交换律、结合律和分配律。

**1.2 行列式的定义、计算和性质**

行列式是一个与矩阵相关的标量值。它表示矩阵的面积或体积，也可以用于判断矩阵的可逆性。行列式的计算可以使用拉普拉斯展开或行列式展开。行列式具有许多性质，如多重性定理和乘法定理。

# 2. 行列式在矩阵论中的应用

行列式在矩阵论中扮演着至关重要的角色，它与矩阵的可逆性、秩和特征值有着紧密的联系。本章将深入探讨行列式在矩阵论中的应用，为理解矩阵的性质和操作提供坚实的基础。

### 行列式与矩阵可逆性

**定义：**一个方阵的行列式不为零，则称该方阵可逆。

**定理：**一个方阵可逆当且仅当其行列式不为零。

**证明：**

* **必要性：**如果一个方阵不可逆，则其行列式为零。这是因为不可逆方阵无法找到其逆矩阵，而行列式为零的方阵无法满足逆矩阵存在的条件。
* **充分性：**如果一个方阵的行列式不为零，则其可逆。这是因为行列式不为零的方阵可以通过高斯消元法化为单位矩阵，而单位矩阵的逆矩阵就是它本身。

**推论：**一个方阵可逆当且仅当其秩等于其阶数。

### 行列式与矩阵秩

**定义：**一个矩阵的秩是指其线性无关的行或列的最大数量。

**定理：**一个矩阵的秩等于其行列式的秩。

**证明：**

* **必要性：**如果一个矩阵的秩小于其阶数，则其行列式为零。这是因为秩小于阶数的矩阵存在线性相关的行或列，而线性相关的行或列的行列式为零。
* **充分性：**如果一个矩阵的行列式不为零，则其秩等于其阶数。这是因为行列式不为零的矩阵可以通过高斯消元法化为单位矩阵，而单位矩阵的秩等于其阶数。

**推论：**一个矩阵的秩等于其非零特征值的个数。

### 行列式与矩阵特征值

**定义：**一个矩阵的特征值是使其与其对应特征向量相乘后仍等于该特征向量的标量。

**定理：**一个矩阵的特征多项式的根是其特征值。

**证明：**

* **必要性：**如果一个标量是矩阵的特征值，则其对应的特征向量与矩阵相乘后仍等于该特征向量。因此，该标量是特征多项式的根。
* **充分性：**如果一个标量是特征多项式的根，则其对应的特征向量与矩阵相乘后仍等于该特征向量。因此，该标量是矩阵的特征值。

**推论：**一个矩阵的特征值等于其行列式的根。

**代码示例：**

%