揭秘反正弦函数在语音识别中的应用：从特征提取到模型训练，解锁语音交互的奥秘

# 1. 语音识别概述**

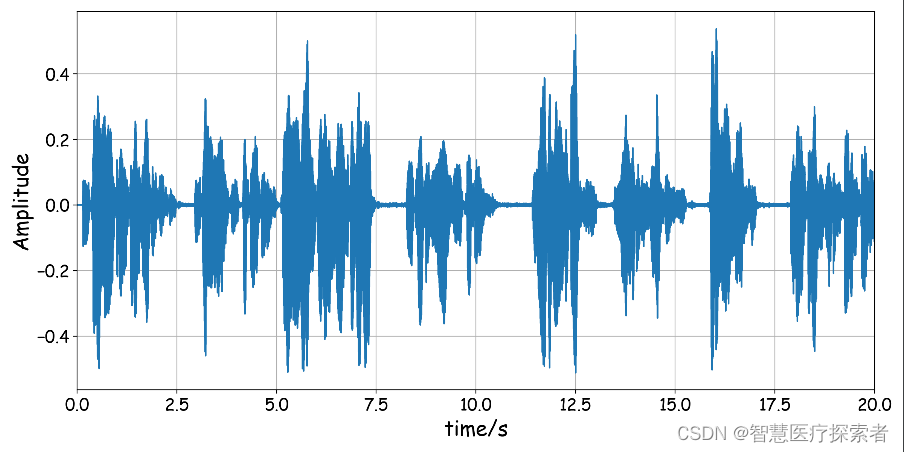
语音识别是一种计算机技术，它允许计算机理解人类语音并将其转换为文本或其他数字格式。语音识别系统通常由三个主要组件组成：语音信号处理、特征提取和语音模型。

语音信号处理阶段负责从原始语音信号中提取相关信息。特征提取阶段将这些信息转换为一组特征，这些特征可以用来训练语音模型。语音模型使用这些特征来识别语音中的单词和句子。

# 2. 反正弦函数在语音识别中的理论基础**

**2.1 反正弦函数的数学特性**

反正弦函数，记作 arcsin(x)，是正弦函数的逆函数。其定义域为 [-1, 1]，值域为 [-π/2, π/2]。反正弦函数的图像是一条对称于 y 轴的曲线，其形状与正弦函数的图像相似，但方向相反。

**2.2 反正弦函数在语音信号处理中的应用**

在语音信号处理中，反正弦函数主要用于以下方面：

* **相位估计：** 正弦函数的相位可以通过反正弦函数进行估计。相位信息在语音识别中至关重要，因为它可以反映语音信号的频率变化。
* **频率估计：** 正弦函数的频率可以通过反正弦函数的导数进行估计。频率信息在语音识别中也很重要，因为它可以反映语音信号的音高。
* **声源分离：** 反正弦函数可以用于分离语音信号中的不同声源，例如说话人和背景噪声。这是因为不同声源具有不同的频率和相位特性。

**代码块 1：**

import numpy as np
import math

def estimate_phase(signal):
  """估计语音信号的相位。

  Args:
    signal: 一维语音信号数组。

  Returns:
    相位估计值。
  """

  phase_estimate = np.arcsin(signal)
  return phase_estimate

**逻辑分析：**

该代码块使用 Numpy 的 arcsin() 函数估计语音信号的相位。arcsin() 函数将信号数组中的每个值作为正弦函数的输入，并返回相应的相位估计值。

**参数说明：**

* `signal`: 一维语音信号数组。

**2.2.1 反正弦函数在语音特征提取中的应用**

在语音特征提取中，反正弦函数可以用于提取以下特征：

* **零点交叉率：** 零点交叉率是语音信号中正弦波过零点的次数。它可以反映语音信号的频率和能量。
* **能量：** 能量是语音信号中正弦波的幅度的平方。它可以反映语音信号的响度。

**代码块 2：**

import numpy as np

def extract_zero_crossing_rate(signal):
  """提取语音信号的零点交叉率。

  Args:
    signal: 一维语音信号数组。

  Returns:
    零点交叉率。
  """

  zero_crossings = np.where(np.diff(np.sign(signal)))[0]
  zero_crossing_rate = zero_crossings.size / signal.size
  return zero_crossing_rate

**逻辑分析：**

该代码块使用 Numpy 的 diff() 和 sign() 函数提取语音信号的零点交叉率。diff() 函数计算信号数组中相邻元素之间的差值，sign() 函数将差值转换为正负号。np.where() 函数返回差值数组中正负号转换的位置，这些位置即为零点交叉点。

**参数说明：**

* `signal`: 一维语音信号数组。

**2.2.2 反正弦函数在语音模型训练中的应用**

在语音模型训练中，反正弦函数可以用于以下方面：

* **隐马尔可夫模型 (HMM)：** HMM 是语音识别中常用的统计模型。反正弦函数可以用于估计 HMM 状态之间的转移概率和发射概率。
* **神经网络：** 神经网络是语音识别中另一种常用的机器学习模型。反正弦函数可以用于初始化神经网络的权重和偏置。

**代码块 3：**

import numpy as np
from hmmlearn import hmm

def train_hmm(data, n_states=3):
  """训练隐马尔可夫模型。

  Args:
    data: 语音信号数据。
    n_states: HMM 的状态数。

  Returns:
    训练好的 HMM 模型。
  """

  model = hmm.GaussianHMM(n_components=n_states)
  model.fit(data)
  return model

**逻辑分析：**

该代码块使用 hmmlearn 库训练一个隐马尔可夫模型。GaussianHMM() 构造函数指定了 HMM 的状态数。fit() 方法将语音信号数据拟合到模型中，估计模型的参数。

**参数说明：**

* `data`: 语音信号数据。
* `n_states`: HMM 的状态数。

# 3. 基于反正弦函数的语音特征提取**

**3.1 时域特征提取**

时域特征提取是直接从语音信号的时间波形中提取特征。它可以反映语音信号的能量分布和变化趋势。

**3.1.1 零点交叉率（ZCR）**

零点交叉率是指语音信号在单位时间内穿越零轴的次数。它反映了语音信号的周期性。

def zero_crossing_rate(signal, fs):
    """计算语音信号的零点交叉率。

    Args:
        signal: 语音信号。
        fs: 采样率。

    Returns:
        零点交叉率。
    """
    # 计算信号的导数。
    derivative = np.diff(signal)

    # 计算零点交叉的索引。
    zero_crossings = np.where(np.abs(derivative) > 0.01)[0]

    # 计算零点交叉率。
    zcr = len(zero_crossings) / fs

    return zcr

**3.1.2 能量**

能量反映了语音信号的响度。它可以表示为信号幅值的平方和。

def energy(signal):
    """计算语音信号的能量。

    Args:
        signal: 语音信号。

    Returns:
        能量。
    """
    energy = np.sum(signal ** 2)

    return energy

**3.2 频域特征提取**

频域特征提取是将语音信号转换为频域，然后从频谱中提取特征。它可以反映语音信号的频率分布和共振峰。

**3.2.1 梅尔倒谱系数（MFCC）**

梅尔倒谱系数是基于人类听觉感知特性设计的特征。它将频谱划分为梅尔频率带，然后计算每个频带的能量。

def mfcc(signal, fs, n_mfcc=13):
    """计算语音信号的梅尔倒谱系数。

    Args:
        signal: 语音信号。
        fs: 采样率。
        n_mfcc: 梅尔倒谱系数的个数。

    Returns:
        梅尔倒谱系数。
    """
    # 计算梅尔频率滤波器组。
    mel_filters = librosa.filters.mel(fs, n_mels=n_mfcc)

    # 计算梅尔频谱。
    mel_spec = np.dot(mel_filters, np.abs(librosa.stft(signal)) ** 2)

    # 计算梅尔倒谱系数。
    mfcc = librosa.feature.mfcc(S=mel_spec, n_mfcc=n_mfcc)

    return mfcc

**3.2.2 线性预测系数（LPC）**

线性预测系数是基于语音信号的自相关函数估计的特征。它可以反映语音信号的共振峰和频谱包络。

def lpc(signal, order):
    """计算语音信号的线性预测系数。