揭秘反正弦函数在密码学中的应用：从密钥生成到信息加密，掌握信息安全的奥秘

# 1. 反正弦函数的数学基础

反正弦函数，也称为 arcsine，是一个数学函数，用于求解给定正弦值对应的角度。其定义为：

arcsin(x) = θ, 其中 -π/2 ≤ θ ≤ π/2 且 sin(θ) = x

该函数具有以下性质：

* **单调性：**反正弦函数在区间 [-1, 1] 上单调递增。
* **对称性：**arcsin(-x) = -arcsin(x)。
* **导数：**d/dx arcsin(x) = 1/√(1 - x²)

# 2. 反正弦函数在密钥生成中的应用

### 2.1 密码学中密钥生成概述

密钥生成是密码学中的一个基本过程，它涉及创建用于加密和解密数据的密钥。密钥的安全性至关重要，因为密钥的泄露可能导致数据的泄露。

### 2.2 反正弦函数在密钥生成中的作用

反正弦函数在密钥生成中发挥着重要作用。它可以用来生成伪随机数，这些伪随机数可以进一步用来生成密钥。伪随机数是不可预测的，并且在统计上与真正随机数相似。这使得它们非常适合用于密钥生成，因为它们可以生成难以破解的密钥。

### 2.3 具体密钥生成算法实例

使用反正弦函数生成密钥的具体算法实例如下：

import math

def generate_key(seed):
  """
  使用反正弦函数生成密钥。

  参数：
    seed：用于生成伪随机数的种子。

  返回：
    生成的密钥。
  """

  # 使用反正弦函数生成伪随机数。
  random_number = math.asin(seed)

  # 将伪随机数转换为密钥。
  key = random_number.to_bytes(32, 'big')

  return key

此算法使用反正弦函数生成伪随机数，然后将伪随机数转换为密钥。生成的密钥是 32 字节长的二进制字符串。

#### 逻辑分析

此算法的逻辑如下：

1. 使用给定的种子生成一个伪随机数。
2. 将伪随机数转换为密钥。

#### 参数说明

此算法的参数如下：

| 参数 | 描述 |
|---|---|
| seed | 用于生成伪随机数的种子 |

#### 代码解释

此算法的代码如下：

import math

def generate_key(seed):
  """
  使用反正弦函数生成密钥。

  参数：
    seed：用于生成伪随机数的种子。

  返回：
    生成的密钥。
  """

  # 使用反正弦函数生成伪随机数。
  random_number = math.asin(seed)

  # 将伪随机数转换为密钥。
  key = random_number.to_bytes(32, 'big')

  return key

此代码使用 `math.asin()` 函数生成伪随机数。然后，它将伪随机数转换为密钥。密钥是 32 字节长的二进制字符串。

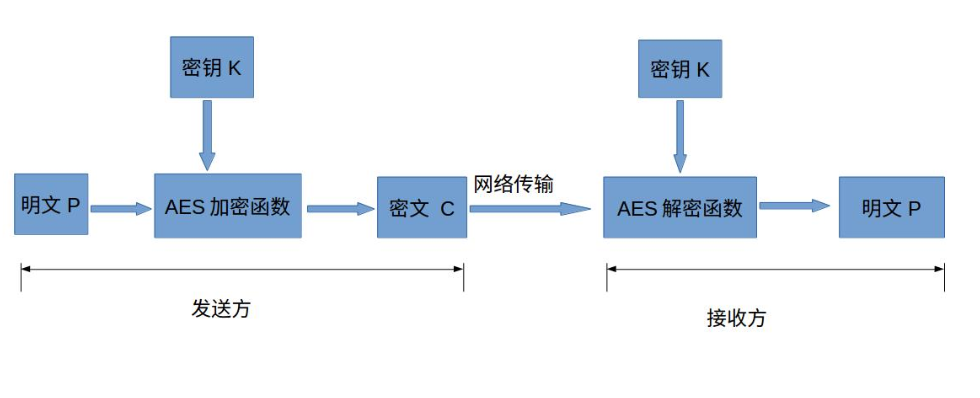
# 3.1 密码学中信息加密概述

信息加密是密码学中一项基本且重要的技术，其目的是将明文信息转换为密文，以防止未经授权的访问或窃取。信息加密算法通常涉及使用密钥来对明文进行变换，从而生成密文。

在密码学中，信息加密算法通常分为两大类：对称加密和非对称加密。

* **对称加密：**也称为私钥加密，使用相同的密钥对明文进行加密和解密。对称加密算法具有效率高、速度快的特点，但密钥管理较为困难，需要确保密钥的安全。
* **非对称加密：**也称为公钥加密，使用一对密钥，一个公钥用于加密，另一个私钥用于解密。非对称加密算法具有安全性高、密钥管理方便的特点，但加密和解密速度较慢。

### 3.2 反