约束优化算法的性能优化技巧：提升算法效率的秘诀

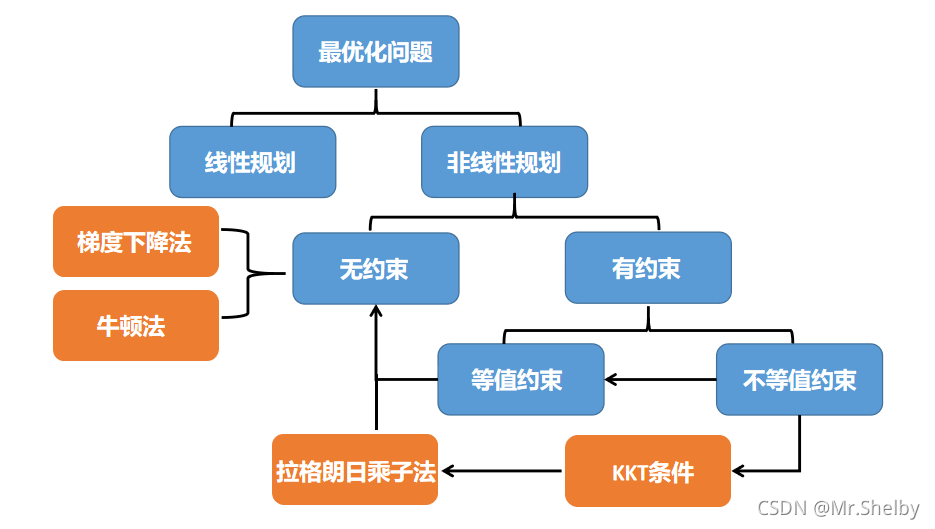
# 1. 约束优化算法概述**

约束优化算法是一种旨在解决带有约束条件的优化问题的算法。与无约束优化算法不同，约束优化算法必须考虑约束条件对可行解空间的影响。约束条件可以是等式或不等式，它们限制了决策变量的取值范围。

约束优化算法的目的是找到满足所有约束条件且优化目标函数的解。这通常是一个具有挑战性的任务，因为约束条件会限制可行解的空间。为了解决这个问题，约束优化算法使用各种技术来探索可行解空间并找到满足约束条件的最佳解。

# 2.1 线性规划和非线性规划

### 2.1.1 线性规划模型和求解方法

**线性规划模型**

线性规划（LP）是一种数学优化技术，用于解决具有线性目标函数和线性约束的优化问题。其一般形式如下：

最大化/最小化 z = c^T x
约束条件：
Ax <= b
x >= 0

其中：

* z：目标函数
* c：目标函数系数向量
* x：决策变量向量
* A：约束矩阵
* b：约束向量

**求解方法**

LP 问题可以通过以下方法求解：

* **单纯形法：**一种迭代算法，通过逐个替换变量来找到最优解。
* **内点法：**一种基于牛顿法的算法，通过迭代更新决策变量来逼近最优解。

### 2.1.2 非线性规划模型和求解方法

**非线性规划模型**

非线性规划（NLP）是一种数学优化技术，用于解决具有非线性目标函数和/或非线性约束的优化问题。其一般形式如下：

最大化/最小化 f(x)
约束条件：
g(x) <= 0
h(x) = 0

其中：

* f(x)：目标函数
* g(x)：不等式约束函数
* h(x)：等式约束函数

**求解方法**

NLP 问题可以通过以下方法求解：

* **梯度下降法：**一种迭代算法，通过沿负梯度方向移动决策变量来逼近最优解。
* **牛顿法：**一种基于二阶导数的算法，通过迭代更新决策变量和海森矩阵来逼近最优解。
* **序列二次规划法：**一种将 NLP 问题转换为一系列二次规划问题的算法。

**代码块：**

import numpy as np
import scipy.optimize as opt

def linear_programming(c, A, b):
    """
    求解线性规划问题

    参数：
    c: 目标函数系数向量
    A: 约束矩阵
    b: 约束向量

    返回：
    最优解
    """

    res = opt.linprog(c, A_ub=A, b_ub=b)
    return res.x

def nonlinear_programming(f, g, h, x0):
    """
    求解非线性规划问题

    参数：
    f: 目标函数
    g: 不等式约束函数
    h: 等式约束函数
    x0: 初始猜测

    返回：
    最优解
    """

    res = opt.minimize(f, x0, constraints=[{'type': 'ineq', 'fun': g}, {'type': 'eq', 'fun': h}])
    return res.x

**逻辑分析：**

* `linear_programming` 函数使用 SciPy 库的 `linprog` 函数求解 LP 问题。
* `nonlinear_programming` 函数使用 SciPy 库的 `minimize` 函数求解 NLP 问题，并指定不等式和等式约束。

# 3.1 约束优化算法在工程设计中的应用

约束优化算法在工程设计中发挥着至关重要的作用，特别是在涉及复杂系统和多目标优化的问题中。

### 3.1.1 结构优化

在结构优化中，约束优化算法用于寻找满足特定约束